深入浅出WebGL - 03 - 仿射变换

刘子弃
1,105 阅读6分钟

本文已参与好文召集令活动，点击查看：后端、大前端双赛道投稿，2万元奖池等你挑战！

本文发布在专栏 深入浅出WebGL 中, 点击查看目录

如没有看过上一章: 深入浅出WEBGL - 02 - 线性变换 建议查看

平移

上篇文章介绍了矩阵可以表示一个线性变换, 并且介绍了剪切、缩放、旋转变换。现在考虑二维的平移变换。还是考虑这个正方形:

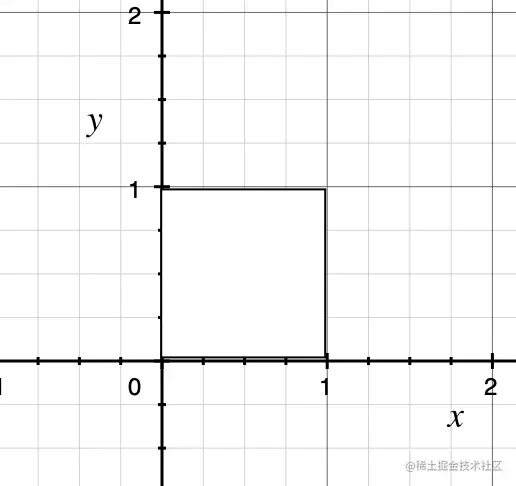
现在想让这个正方形向右移动一个单位长度, 也就是[1,1]T[1,1]^T(列向量的转置, 等同于竖着写) 会变化到 [2,1]T[2, 1]^T 很容易就能想到这个可以用向量加法表示, 即把正方形内所有的点的横坐标都加一。这样做的话有几点坏处:

1. 平移操作无法与其他变换复合

因为剪切缩放旋转都是矩阵乘法, 复杂运动就可以直接乘好多个矩阵就可以,也可以先把矩阵相乘, 得到一个变换矩阵。但是如果变化过程中间断的插入几个矩阵加法，这件事情就不那么好算了。

2. 无法表示平移到无穷远

如果用矩阵加法的话，平移到无穷远这件事就无法表示了。

有什么方法能把平移也用矩阵乘法表示呢?

有，我们需要引入 齐次坐标。

齐次坐标

第一次引入其次坐标的概念可能有些理解的不太直观。简单来说，就是用多一个维度的坐标来表示当前的坐标。比如二维的点[3,2]T[3,2]^T的一种其次坐标表示方法就是[3,2,1]T[3,2,1]^T。 他们是同一个点的不同的坐标表示。我们经常用的表示方法是笛卡尔坐标, 这种多一维的表示方法是齐次坐标。

齐次坐标跟笛卡尔坐标是可一互相转换的, 二维和三维的例子:

[x,y]T=[x/w,y/w]T:=[x,y,w]T [x,y]^T = [x/w, y/w]^T := [x,y,w]^T
[x,y,z]T=[x/w,y/w,z/w]T:=[x,y,z,w]T [x,y,z]^T = [x/w, y/w, z/w]^T := [x,y,z,w]^T

可以看到, 一个具体的点用齐次坐标有无数种表示方法, 比如[3,2,1]T[3,2,1]^T, [6,4,2]T[6,4,2]^T, [9,6,3]T[9,6,3]^T 都是点[3,2]T[3,2]^T的合法的齐次坐标写法。 换算的时候用w除正好都是[3,2]T[3,2]^T。我们称某个点的一堆齐次坐标表示方法互相之间是 同质(homogeneous) 的。 含义也就是说这些点都是相同性质的，表示的都是同一个东西。

齐次坐标 (homogeneous coordinates) 表示的就是同质的坐标的意思

为什么图形学都用齐次坐标表示点呢？为什么齐次坐标就可以把平移变成矩阵乘法来运算呢？下面举个例子:

还是点[3,2]T[3,2]^T 我想把他移动到[4,2]T[4,2]^T这个位置。也就是沿x轴向右👉平移一个单位长度。我们得这个点的齐次坐标表示 [3,2,1]T[3,2,1]^T, 然后定义变换矩阵:

[101010001]\left [ \begin{matrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right]

我们进行运算:

[101010001][321]=[421]\left [ \begin{matrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right] \left [ \begin{matrix} 3 \\ 2 \\ 1 \end{matrix} \right] = \left [ \begin{matrix} 4 \\ 2 \\ 1 \end{matrix} \right]

得到了新的点的齐次坐标表示[4,2,1]T[4,2,1]^T, 对应的笛卡尔坐标就是同时除w得到[4,2]T[4,2]^T。

上面演示了齐次坐标的确可以让我们用矩阵乘法表示平移, 但是我相信大家还是有问题: 为啥加了一项就这么神奇了？就可以表示平移了？ 其实我们能观察到多加的一项正好乘矩阵最右排, 可以控制跟x或者y相加。 下面以更直观的方式理解上面的过程:

单纯看上面的例子, 他有两个含义: 一种是代表二维空间下以齐次坐标方式表示的平移变换,同时还是三维空间下的笛卡尔坐标系下的某种线性变换!我们接下来看一下同样的矩阵在三维笛卡尔坐标系下是怎么样的变换。

同样在三维坐标系下放一个边边长为一个单位的立方体:

我相信你能想象到这个立方体的各个顶点的坐标是多少。首先我们观察底平面的坐标，由于底平面的坐标z=0, 例如[1,1,0]T[1,1,0]^T左乘如上矩阵后不变。所以我们得到底平面不变，然后观察上平面的点, 上平面由于z=1, 左乘矩阵后得到的坐标的x都+1了。中间的点z都是零点几, 所以都是x加上零点几的数字。 所以变换后这个方块变成了这样:

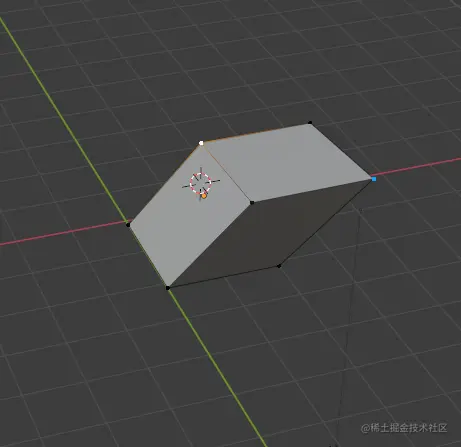
也就是说，正方块的上层沿被推了出去, 这就是三维的剪切变换呀! 然后我们进行这样的操作:

单纯看顶层并把他“拍扁”到“地面”，再把结果跟变换之前的顶层“拍扁”到“地面”的结果做对比。我们就得到了一个二维平移变换！我们通过进行三维的剪切变换然后降维只取他一层的二维信息就得到了二维的平移变换。

假设上面的方块边长是2，进行计算后会得到(可以带一个试试)最顶面会缩放成为1*1 的大小(因为/w的时候是除2了), 所以结果是一样的。其实11正方形内零点几的平面拿出来“拍到地面”都会是1* 1的大小。这时候也可以想象很大的立方体, 拍到地面都是11的。所以对应二维的一个1*1的方块有无数个立体空间的“片”对应着它，这些“片”也就是同质的。

仿射变换

我们把线性变换和平移变换加起来叫做仿射变换。方便进行仿射变换的操作当然是用齐次坐标的方法来表示一个坐标。 在三维空间中。我们用[x,y,z,w]T[x,y,z,w]^T 表示一个点。对应的变换矩阵当然是4*4的。常见变换如下:

不变
[1000010000100001]\left [ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]
平移
[100x010y001z0001]\left [ \begin{matrix} 1 & 0 & 0 & x \\ 0 & 1 & 0 & y \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \end{matrix} \right]
缩放
[n0000n0000n0000n]\left [ \begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n & 0 \\ 0 & 0 & 0 & n \end{matrix} \right]
旋转(绕z轴，x轴，y轴)
[cos(θ)−sin(θ)00sin(θ)cos(θ)0000100001][10000cos(θ)−sin(θ)00sin(θ)cos(θ)00001][cos(θ)0−sin(θ)00100sin(θ)0cos(θ)00001]\left [ \begin{matrix} cos(\theta) & -sin(\theta) & 0 & 0 \\ sin(\theta) & cos(\theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \left [ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & cos(\theta) & -sin(\theta) & 0 \\ 0 & sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right] \left [ \begin{matrix} cos(\theta) & 0 & -sin(\theta) & 0 \\ 0 & 1 & 0 & 0 \\sin(\theta) & 0 & cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]

css transform

我们都熟悉css3 新添加了一个transform 属性我们可以用他来做动画。并且它提供了缩放、平移、旋转等方便的操作。其实细心的同学也知道他也可以写matrix为值。只不过看起来要传一堆数字。看起来怪怪的。其实这个就是上面所说的4*4的矩阵。

对应的mdn: developer.mozilla.org/zh-CN/docs/…

我们看到mdn给的写法:

     transform: matrix3d(
      1,0,0,0,
      0,1,0,0,
      0,0,1,0,
      50,100,0,1
    )

这个写法跟上面的咱们讲的矩阵是转置关系。以左上右下为轴旋转一下看起来就跟上面讲的矩阵一样了。如上面的矩阵是平移。

问题

  1. 可以尝试玩一玩css transform的matrix写法,实现一些动画吧！
  2. 如何把一个点移动到无穷远处呢？
avatar
文章
阅读
粉丝