本文已参与好文召集令活动,点击查看:后端、大前端双赛道投稿,2万元奖池等你挑战!
本文发布在专栏 深入浅出WebGL 中, 点击查看目录
如没有看过上一章: 深入浅出WebGL - 01 - 点、向量、矩阵 建议查看
下面的公式一点都不难, 希望能看进去。而不是 收藏 = 会了 ... 虽然我知道没有什么人收藏... 啊不...应该是都没什么人看...
点的运动 - 向量
首先我们来说明一下点的运动这件事情。
在某坐标系下的点和向量都可以用一个竖着写的⎣⎡xyz⎦⎤ 去表示,当然二维点或向量是[xy] 去表示的。向量表示的是一个点的运动方向的,所以一个向量是具有长度和方向的。而点的坐标仅仅表示在某个坐标系下一个具体的位置。
怎么理解向量是点的运动呢? 这里我们回顾一下上篇文章中的一些运算:
- p~ + v
这代表这个点沿着这个向量的方向移动, 移动距离为向量的长度, 例如:
点[11] + 向量 [21] 得到的是点[32]
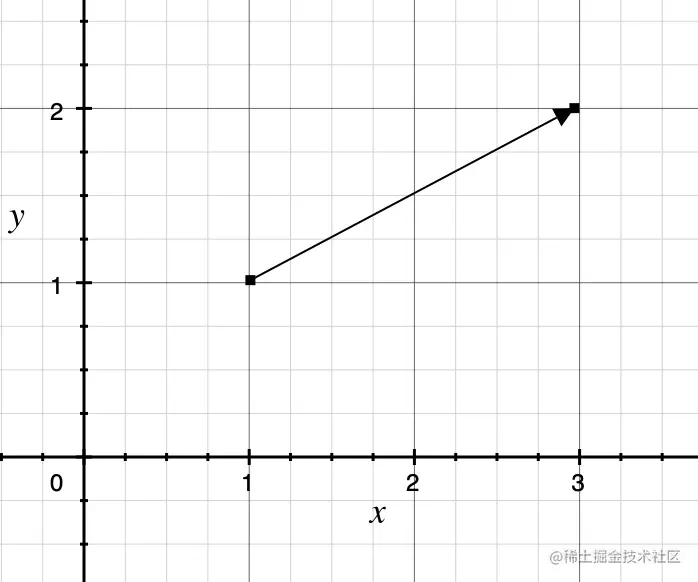
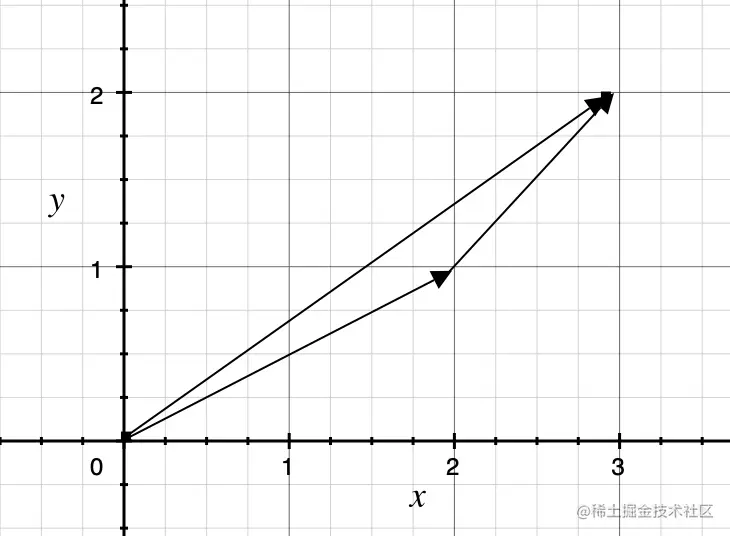
- p~1 - p~2
这个结果得到的是一个向量, 向量的方向是从点2指向点1
- v1 + v2
得到的结果是一个新的向量, 即两个代表点运动的向量相加得到了全新的一个代表点运动的向量, 新向量的运动结果跟之前两个向量代表的运动结果的叠加是相同的:
- 向量的点积
向量的点积公式:
v1⋅v2=∣∣v1∣∣∗∣∣v2∣∣∗cos(θ)
我们用 ∣∣v1∣∣ 代表向量 v1的长度, θ表示两个向量的夹角。所以两个向量的点积得到的是一个数字, 那么点积有什么含义呢?首先我们可以求一个向量到另一个向量的投影长度 v1⋅normalize(v2)得到的就是 v1 在向量v2方向上的投影长度。
【注】 假设 v3 = normalize(v1) 代表取此向量上的单位向量, 即v3 与 v2方向相同, 长度为1。 即有 ∣∣v3∣∣=1。
【再注】normal 一般代表法向, 跟normalize 代表的含义并不相同。
我们还可以用点积判断两个向量的夹角。如果取两个向量的normalize再点乘, 得到的就是夹角的cos值。
normalize(v1)⋅normalize(v2)=cos(θ)
比如判断光线和法线normalize 点积结果可以判断当前三角面跟光照的角度。 或者某向量点乘自己可以得到自己的长度的平方。
- 向量的叉积
向量的叉积公式:
v1⋅v2=∣∣v1∣∣∗∣∣v2∣∣∗sin(θ)∗nn
得到的结果是一个向量, 在三维空间中表示的是垂直于v1和v2的向量, 方向是根据右手定则确定的。
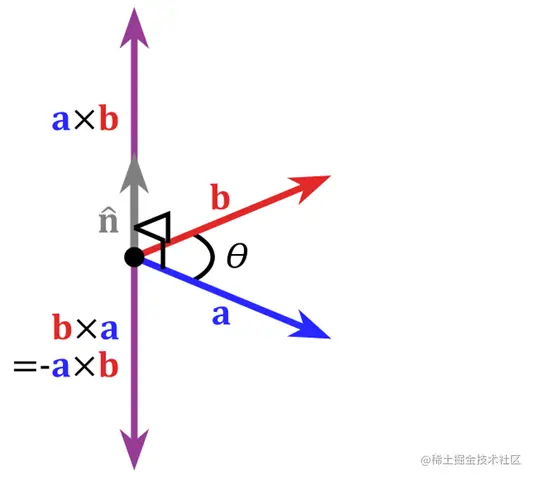
叉积可以帮助我们求法向或者计算相机的lookup 等等。
线性变换
我们现在关注二维坐标系下的矩阵变换。
{2x+1y3x+2y
形如这样的多项式组可以用矩阵来表示:
[2312]
一个向量左乘一个矩阵其实就是把向量的每一个分量的数字带到这个多项式的对应变量中去计算
[2312][12]=:{2x+1y3x+2yx=1,y=2;x=1,y=2;=:[47]
这样,上面这个矩阵的作用就是把[12] 变到了 [47] 这个位置。 同时也可以观察到新向量的每一个分量的值是变化之前的向量的每个方向上的分量的值的线性组合。
坐标系 Wt 下的向量 v 是 此坐标系每个分量的线性组合。 在二维坐标系中,有x, y 两个轴, 我们取 x 和 y 作为基向量。 则:
v=[xy][n1n2]
上面👆式子可以简写成:
v=Wtn
定义线性变换λ(x),则:
λ(v)=λ([xy][n1n2])=[λ(x)λ(y)][n1n2]
变化作用在坐标系的每一个分量上
其中λ(n) 的每一项为:
λ(x)=[xy][M11M12]
同上面说过的新向量的每一个分量的值是变化之前的向量的每个方向上的分量的值的线性组合
则最终的变换可以用矩阵表示:
[xy][M11M12M21M22][c1c2]
简写为:
Wtn=WtMn
矩阵变换都是线性变换
接下来我们分析几个典型的矩阵变换
剪切变换
有请我们的正方形:
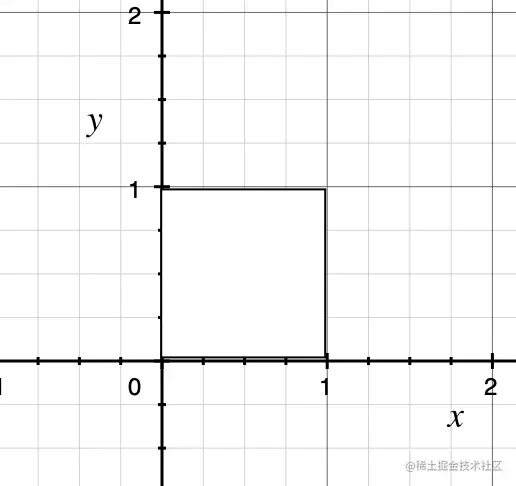
这个正方形的四个顶点我相信你一定能看出来, 那么接下来我们定一个变换,用矩阵M表示:
M=[1011]
尝试正方形的四个顶点分别带入这个变换,则:
M=[1011][11]=[21]
省略三个点, 可以自行算一下。
经过你的计算,可以发现最后的结果是变成了一个平行四边形。 这种变换叫做剪切变换。
缩放变换
还是上面的正方形, 可以计算一下乘M=[2002] 后的结果,也可以看看乘单位矩阵M=[1001] 得到的结果什么样的。
旋转变换
上面两个的变换比较直观, 现在我们来研究一下如何用一个二维矩阵旋转一个二维坐标系下的向量。
首先, 先上图(网图侵删):
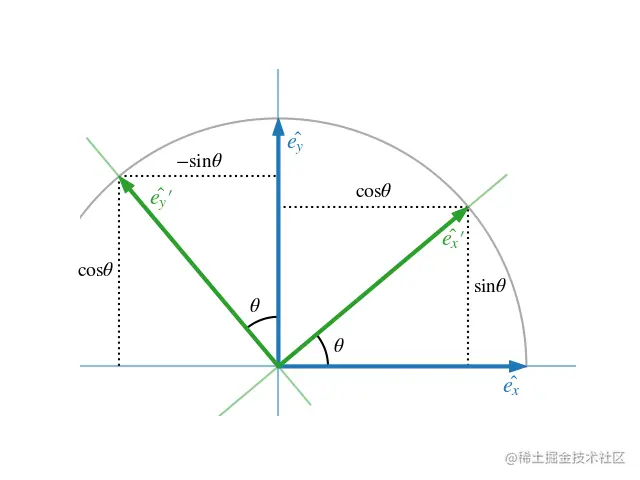
可以想象一下, 我们旋转坐标系的基向量, 带着里面的点也旋转这样从原坐标系看去就是点旋转了。
可以从图中明显的看到,原来的 [10] 变成了[cos(θ)sin(θ)], [01] 变成了 [−sin(θ)cos(θ)] 。
取一个具体的点:[32] 他代表的含义就是这个向量由三倍的x轴单位向量和2倍的y轴单位向量组合而成的一个向量: 3x+2y。 那么旋转后的点相对于旋转后的坐标系也是一样的: 3x′+2y′。
如图,又有:
x′=[cos(θ)sin(θ)]y′=[−sin(θ)cos(θ)]
得:
3[cos(θ)sin(θ)]+2[−sin(θ)cos(θ)]
即:
[cos(θ)sin(θ)−sin(θ)cos(θ)][32]
所以二维坐标系中的旋转矩阵表示为[θ是以坐标系原点逆时针方向旋转θ度]:
[cos(θ)sin(θ)−sin(θ)cos(θ)]
以上是比较典型的矩阵变换, 当然这些矩阵的变换可以叠加, 一个向量多左乘一个矩阵就是进行一次变换, 矩阵乘法满足结合律, 所以可以先把两个矩阵的乘法结果算出来。新的矩阵就代表好多个变化的叠加了。
思考问题
- 三维的缩放旋转剪切是怎么表示的呢? (下篇文章内容)
- 我想让上面那个方块围绕着自己的原点旋转该怎么操作呢?(多个变化的复合)
- 如果我想平移这个正方形可以用矩阵乘法的形式表示么? (下篇文章内容)
- 屏幕上有三个点围成一个三角形, 随机再取一个点n, 如何判断点n是否在三角形内部? 向量叉积
参考
- 线性代数及其应用
- Foundations of 3D Computer Graphics