目录
- 动态规划解决了什么
- 什么是动态规划
- 典型的动态规划
1. 动态规划解决了什么
我们知道的思想就是将大问题拆分成小问题进行攻破;
比如钢条切割问题:
给定一段长度为n的钢条和如下的价格表,求切割钢条方案,使得收益最大
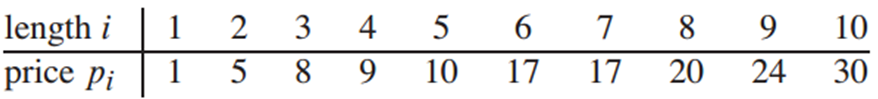
我们很容易想到通过递归进行求解:
假设price(x)代表长度x的钢材的最大收益,我们很容易将问题进行递归分解:
price(n) = max(pi, price(1)+price(n-1), price(2)+price(n-2),....,price(n-1)+price(1) );
比如,我们求解一根长度为4的钢材的切割方式:
就是求取各种组合的最大利益
price(4) = max(p4, price(1) + price(3), price(2) + price(2), price(3) + price(1));
那么接下来就是求解,price(3)、price(2)、price(1)的问题了;
这种自顶向下分解递归的方式肯定是可以解决这个钢条切割的问题的,但是有没有缺陷?
有的,还不小,就是效率问题。
随着x的增大,递归的效率会越来越低,运行速度会很慢,因为什么?
因为它在反复求解相同的问题
在price(3)时,其已经计算过3的最优解了,且2、1的肯定也有了;
作为人类,我们自然而然就会将这个结果记住,并用于下次计算;
但是递归不会,在price(4)的时候,其仍然还会计算price(3),price(2),price(1),不管是不是上次递归已经计算过了。
那么解决这个问题的很简单的办法是什么?
没错,就是
将先前解决的子问题,进行存储,以减少重复计算!
这就是
好了,貌似我们讨论到现在都是说的递归问题,其实呢,到目前为止,我们已经讲完了动态规划的本质:
2. 什么是动态规划
1.动态规划是通过组合子问题的解来解决原问题
2.动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题
3.动态规划算法对每个子子问题只求解一次
4.动态规划通常用来求解最优化问题
动态规划算法:
1.刻画一个最优解的结构特征
2.递归的定义最优解的值
3.计算最优解的值,通常自底向上
4.利用计算出的信息构造一个最优解
好了,让我们用动态规划解一下钢条切割问题:
1.刻画一个最优解的结构特征
递归法中已经刻画的很清楚了
2.递归的定义最优解的值
公式也在上面写过了
3.计算最优解的值,通常自底向上
通过带备忘的自顶向下递归法,我们成功的比较高效的解决了钢铁切割的问题,这也是动态规划的一种方式,有没有其他方式?
有的,对应于自顶而下,我们采用自底而上的方式,将子问题按照从小到大的顺序进行求解,当然还是得有备忘机制。
大部分情况下,自顶而下和自底而上的效率是近似的;但是呢,在某些特殊情况,自顶向下方法并未真正的递归考察所有可能的子问题;而且自底向上也没有频繁的递归函数的开销;
所以,一般动态规划都是采用自底向上的方法,将复杂的问题,变成了简单的多项式相加。
4.利用计算出的信息构造一个最优解
这条就更简单了,既然你算法都写出来了,在算法的途中,加上最优解的存储及输出就可以了,
比如动态规划钢铁切割问题,在算法最初,我们关心的是price(n),计算出最佳的收益;
最后我们只要在编写出的算法中,加上输出钢铁的分割就可以了。
3. 典型的动态规划
钢铁切割问题本身就是个典型的动态规划,除了这个例子,还有:
最长公共子序列
最优二叉搜索树
矩阵链乘法
....
不管是什么问题,本质上我们都是通过层层分解子问题,并进行组合;
如果这个问题,满足上述特性,那么动态规划就是这些问题可能的解决方法之一。
某些问题是否适用于动态规划算法,你可以从如下角度:
1.是否具有最优子结构性质
如果一个问题的最优解,包含其子问题的最优解
2.具有重叠子问题性质
问题的递归算法会反复求解相同的子问题
算法的精髓在于,其没有最好,只有最合适
其他相关章节
算法相关文章之一:《简单说说二叉搜索树》
算法相关文章之二:《B树,一点都不神秘》
算法相关文章之三:《B树很简单,插入so easy》
算法相关文章之四:《什么是动态规划》
算法相关文章之五:《LCS,给你一个不一样的模糊匹配》