B树，一点都不神秘

埃里克拓荒
1,017 阅读3分钟 
                        这是数据库索引相关内容的第一篇

B树

目录：

  1. 什么是B树
  2. B树的最小度数
  3. B树的高度
  4. 什么情况下使用B树
  5. B树的插入
  6. B树的删除

正文：

  1. 什么是B树

    1>  是一种平衡搜索树
2>  为磁盘或者其他直接存储的辅助存储设备设计
3>  类似于红黑树，但是更降低磁盘操作I/O
4>  节点分为内部节点（非叶子节点）和叶子节点
5>  节点可以不止一个关键字
6>  假设节点中的关键字个数为n,则该节点的孩子数一定是n+1
7>  每个节点内部的排序一定是从左到右增大（如下图30 < 80,50 < 60)
8>  假设节点x的关键字的个数为n,从左到右为x1,x2,...xn(如下图n=2,x1=50,x2=60)
    由第6>条得知其孩子数为n+1,从左到右为c1,c2,...cn+1(如下图c1=(35,40),c2=55,c3=70)
    那么排序规则一定是c1<x1<c2<x2<..xn<cn+1
9>  每个叶子节点一定具有相同的深度，即树的高度是一致的。
10> 每个节点关键字的个数有上限和下限，取决于树设定的最小度数t。
		t -1 <= n <= 2t -1
	根节点不受最小t -1的限制，如果树非空，根节点至少有1个关键字

典型的B树如下图

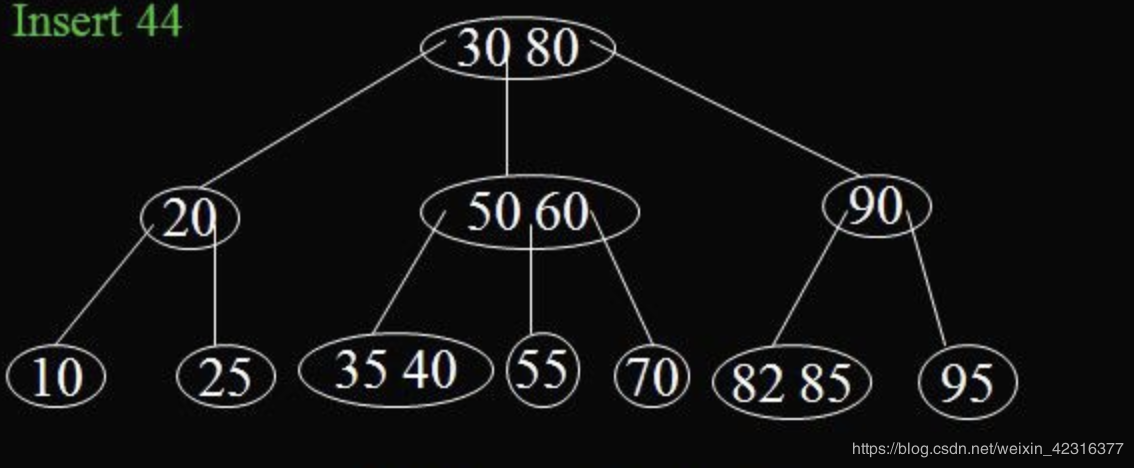
在这里插入图片描述
2. B树的最小度数

	1> 每个节点关键字的个数有上限和下限，取决于树设定的最小度数t。
			t -1 <= n <= 2t -1
	   根节点不受最小t -1的限制，如果树非空，根节点至少有1个关键字
	
	2> 当一个节点恰好有2t-1个关键字，则该节点是满的（在插入B树时用到该概念）
	3> 当一个节点恰好是t-1个关键字时，则该节点是最小状态（在删除B树时用到该概念）

3. B树的高度

为什么我们要关心B树的高度，因为B树主要是为磁盘访问设计的，B树的高度与磁盘存取次数成正比。

因为根节点最小关键字数目为1，其他节点最少为t-1，则树上的关键字个数n满足:

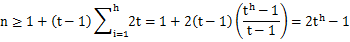
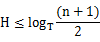
在这里插入图片描述
则树的高度满足：

在这里插入图片描述
所以随着t的增大，h减少，磁盘的存取次数也减少。

4. 什么情况下使用B树

如第一节所述，B树是为磁盘或者其他直接存储的辅助存储设备设计的。
典型的B树使用场景就是数据库。

从树的高度公式可以看出，t越大，即节点内关键字越多，树的高度越小，磁盘存取次数越少。

树的节点关键字越多，那么多少合适呢？

其实，节点中关键字，就是磁盘一次要读取的大小，以磁盘的页为单位，磁盘一般一次会加载1个或多个页，1页的大小一般在4k~8k

所以关键字少了，一次磁盘读取，会造成浪费；关键字多了，一次磁盘读取就读不下。

所以设置合理的t值很重要。并且在动态插入删除中要保证B树也符合B树的上述特征，来满足应用场景需要。

关于B树的插入和删除，下章再说...

写在最后，学好B树还有助于我们理解数据库设计


                                其他相关章节

数据库索引相关文章之一：《B树，一点都不神秘》
数据库索引相关文章之二：《B树很简单,插入so easy》
数据库索引相关文章之三：《索引》
数据库索引相关文章之四：《什么索引算是好的索引》
数据库索引相关文章之五：《如何发现及替换不合适的索引》
数据库索引相关文章之六：《索引总结》

avatar
文章
阅读
粉丝