算法系列篇章-可以参照如下顺序阅读
题目:有一个主串S:ababcababa,模式串T:ababa,请找到模式串在主串中第一次出现的位置(提示:不需要考虑字母大小写问题,字母均为小写字母)
1. BF算法
BF(Brute Force)算法是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串P的第一个字符进行匹配,若相等,则继续比较S的第二个字符和P的第二个字符;若不相等,则比较S的第二个字符和P的第一个字符,依次比较下去,直到得出最后的匹配结果。BF算法是一种蛮力算法。
1.1 BF算法思路分析
举例说明
给定串S: ababcababa 模式串T: ababa
BF算法的匹配步骤如下:
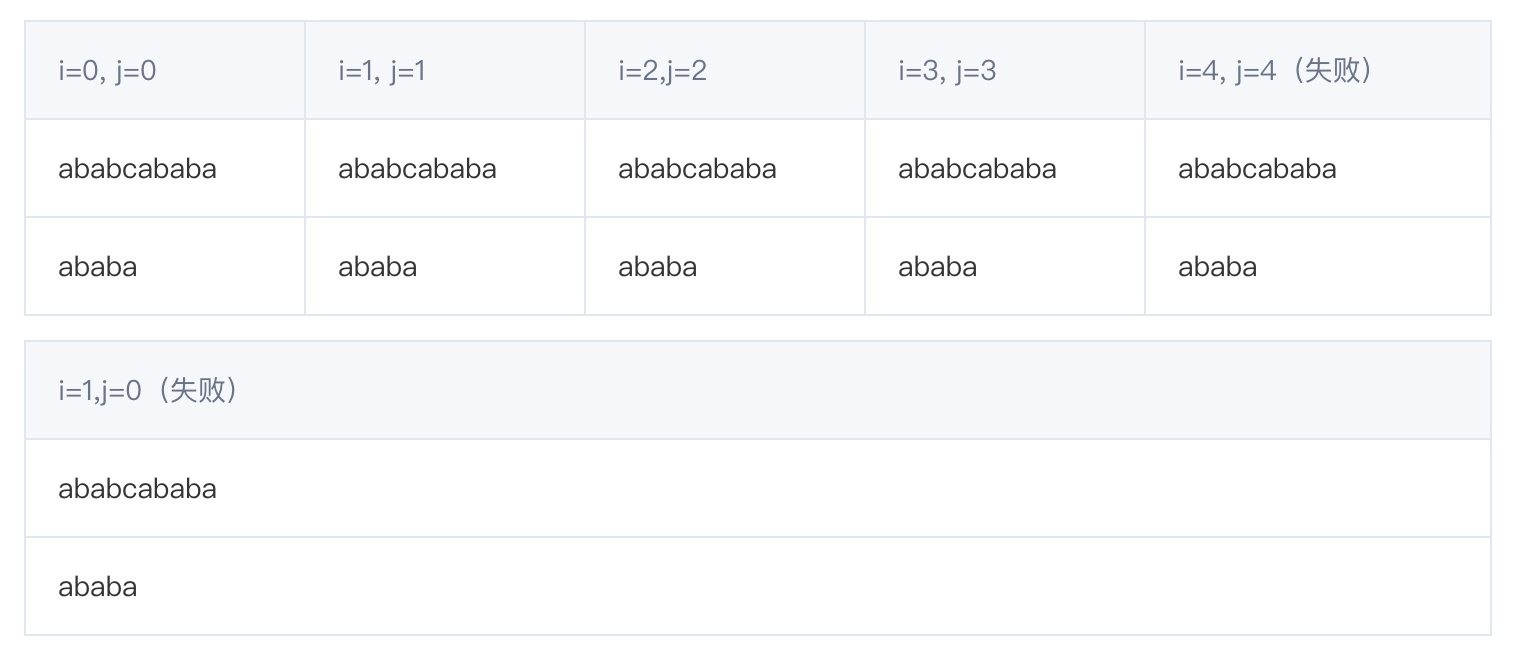
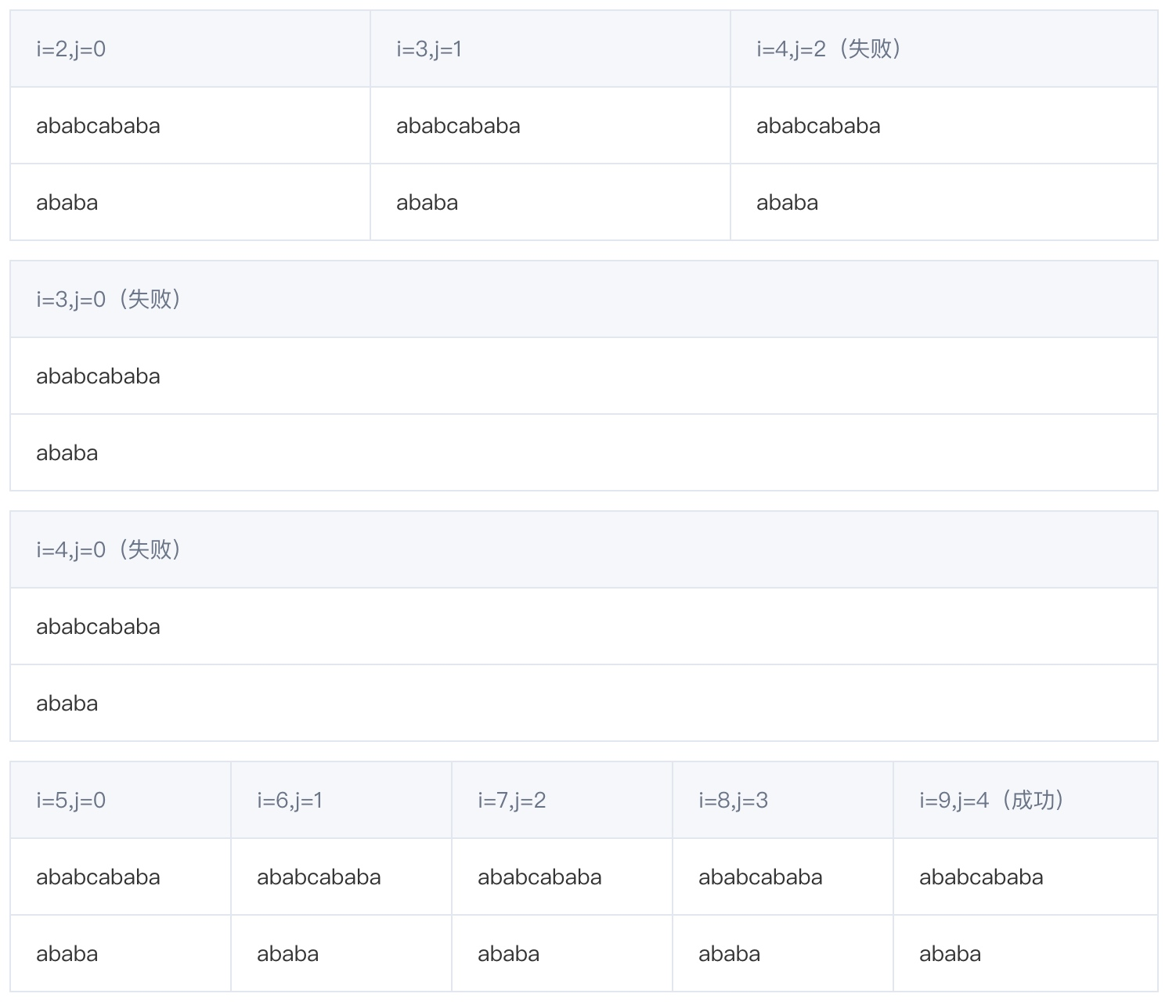
1.2 BF算法代码实现
// 字符串匹配BF算法
int matchStringBF(char *S, char *T, int pos){
// 记录制定开始匹配的位置
int i = pos;
// 记录匹配串的匹配位置
int j = 0;
// 循环遍历对比模式串和主串
while (i < strlen(S) && j < strlen(T)) {
if(S[i] == T[j]){ // 相等就继续向前匹配
i++;
j++;
}else{ // 如果不想等 匹配位置回溯
i = i - j + 1;
j = 0;
}
}
// 判断是否匹配到
if(j == strlen(T)){
return i-j;
}
// 没有匹配到
return -1;
}
1.3 结果预期
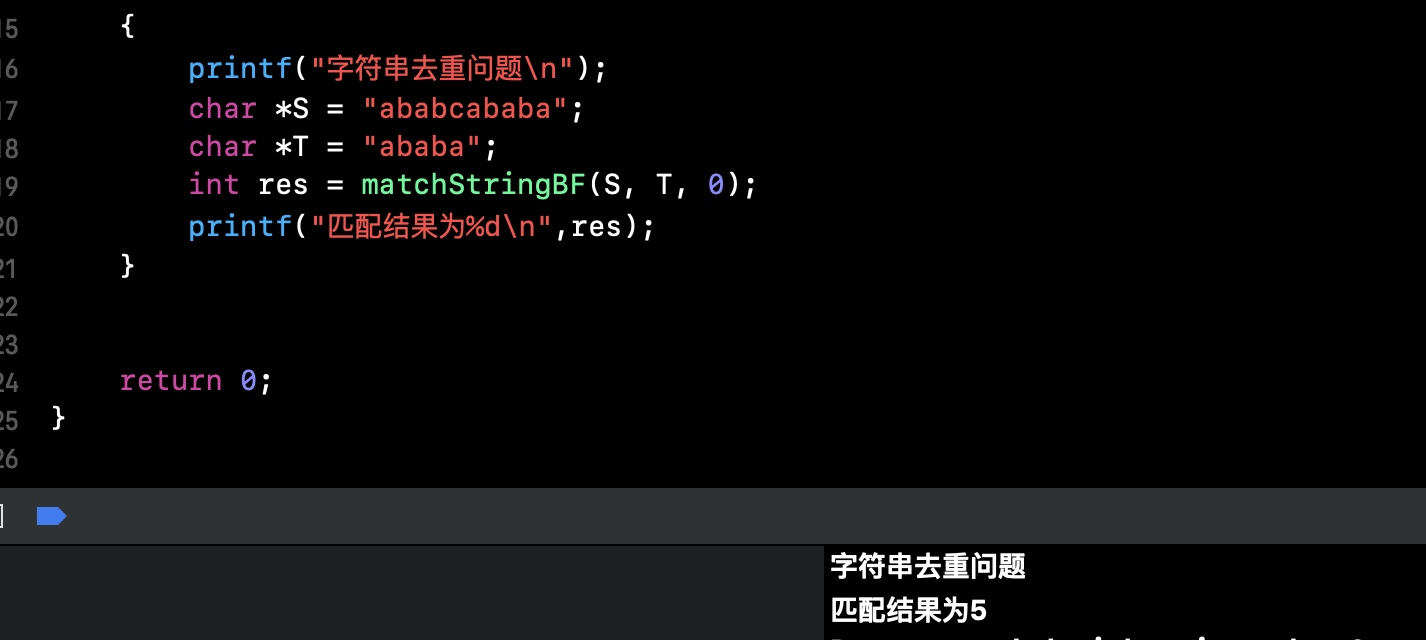
2 RK算法
如果两个字符串hash后的值不相同,则它们肯定不相同;如果它们hash后的值相同,它们不一定相同。
RK算法的基本思想就是:将模式串P的hash值跟主串S中的每一个长度为|P|的子串的hash值比较。如果不同,则它们肯定不相等;如果相同,则再诸位比较之。
2.1 RK算法分析
2.1.1 优势
- 1.把母串以模式串的长度等分,然后比较子串的哈希值
- 2.一边计算子串的哈希值,一边比较,并不是先计算出所有的子串的哈希值,再去比较
2.1.2 RK算法核⼼思想
将不同的字符组合能够通过某种公式的计算映射成不同的数字!
例如
比较 “abc” 与 “cde” ; 比较 123 与 456; 是一样的吗?
657 = 6 *10 * 10 + 5 * 10 + 7 * 1
657 = 6 * 10^2 + 5 *10^1 + 7 *10^0
所以字母换算成哈希值
"cba" = 'c' * 26 * 26 + 'b' * 26 + 'a' * 1
= 2 * 26 * 26 + 1 * 26 + 0 * 1
= 1378
RK 算法核⼼思想
"cba" = c * 26^2 + b * 26^1 + a * 26^0
= 2 * 26^2 + 1 * 26^1 + 0 * 26^0
= 1352 + 26 + 0
= 1378
2.1.3 子串哈希值求解规律
相邻的2个子串 s[i] 与 s[i+1] (i表示子串从主串中的起始位置,子串的长度
都为m). 对应的哈希值计算公式有交集. 也就说我们可以使用s[i-1]计算出s[i]的哈希值;
s[i] = 1 * 10^2 + 2 * 10^1 + 7 * 10^0
s[i+1] = 2 * 10^2 + 7 * 10^1 + 4 * 10^0
s[i+1] = 10 * (127 - 1 * 10^2 ) + 4
s[i+1] = 10 * (s[i] - 1 * 10^2 ) + 4
s[i+1] 实现上是上一个s[i]去掉最高位数据,其余的m-1为字符乘以d进制. 再加上最后一个为字符得到;
2.2 代码实现
#define d 26
// 判断两个字符串是否想等
int isEuqalString(char *S, char *P, int n, int m , int pos){
int i,j;
for (j = pos, i = 0 ; i < m; j++,i++) {
if (S[j] != P[i]) {
return 0;
}
}
return 1;
}
// 求 d^(m-1)
int getHValue(int m){
int res = 1;
for (int i = 1; i < m; i++) {
res = d * res;
}
return res;
}
// RK算法
int matchStringRK(char *S, char *P){
// 1.记录两个字符串的长度
int m = (int)strlen(P);
int n = (int)strlen(S);
// 2.记录模式串和子串的哈希值
long long A = 0;
long long ST = 0;
int hValue = getHValue(m);
// 3.求解模式串和子串的哈希值
for(int i = 0; i < m; i++){
A = d * A + (P[i] - 'a');
ST = d * ST + (S[i] - 'a');
}
// 4.遍历所有子串
for (int j = 0; j <= n - m; j++) {
if (A == ST) { // 此处需要解决可能产生的哈希冲突
if (isEuqalString(S, P, n, m, j) == 1) return j;
}
ST = ((ST - hValue*(S[j]-'a'))*d + (S[j+m]-'a'));
}
return -1;
}
2.3 结果分析
3. KMP算法
KMP算法是D.E.Knuth、J.H.Morris和 V.R.Pratt三位神人共同提出的,称之为Knuth-Morria-Pratt算法,简称KMP 算法。该算法相对于Brute-Force(暴力)算法有比较大的改进,主要是消除了主串指针的回溯,从而使算法效率有了某种程度的提高。
3.1 思路分析
一般匹配字符串时,我们从目标字符串str(假设长度为n)的第一个下标选取和ptr长度(长度为m)一样的子字符串进行比较,如果一样,就返回开始处的下标值,不一样,选取str下一个下标,同样选取长度为n的字符串进行比较,直到str的末尾(实际比较时,下标移动到n-m)。这样的时间复杂度是O(n*m)。
KMP算法:可以实现复杂度为O(m+n);
3.2 next回溯数组求解思路
考察目标字符串ptr:ababaca:
- 这里我们要计算一个长度为
m的转移函数next; next数组的含义就是一个固定字符串的最长前缀和最长后缀相同的长度;
比如:
abcjkdabc,那么这个数组的最长前缀和最长后缀相同必然是abc;
cbcbc,最长前缀和最长后缀相同是cbc;
abcbc,最长前缀和最长后缀相同是不存在的;注意最长前缀:是说以第一个字符开始,但是不包含最后一个字符。比如aaaa相同的最长前缀和最长后缀是aaa。
- 在求解next数组的4种情况:
// i为前缀位置 j为后缀位置
1. 默认next[1] = 0; i=0,j=1;
2. 当 i=0时,表示当前的比应该从头开始.则i++,j++,next[j] = i;
3. 当 T[i] == T[j] 表示2个字符相等,则i++,j++.同时next[j] = i;
4. 当 T[i] != T[j] 表示不相等,则需要将i 退回到合理的位置. 则 i = next[i];
- 对于目标字符串
ptr="ababaca",长度是7,所以next[0],next[1],next[2],next[3],next[4],next[5],next[6]分别计算的是a,ab,aba,abab,ababa,ababac,ababaca的相同的最长前缀和最长后缀的长度。由于a,ab,aba,abab,ababa,ababac,ababaca的相同的最长前缀和最长后缀是“”,“”,“a”,“ab”,“aba”,“”,“a”,所以next数组的值是[0,1,1,2,3,4,1];
3.3 next代码实现
//----字符串相关操作---
/* 生成一个其值等于chars的串T */
typedef char String[MAXSIZE+1]; /* 0号单元存放串的长度 */
void StrAssign(String T,char *chars)
{
int i;
if(strlen(chars)>MAXSIZE)
return;
else
{
T[0]=strlen(chars);
for(i=1;i<=T[0];i++)
T[i]=*(chars+i-1);
}
}
//注意字符串T[0]中是存储的字符串长度; 真正的字符内容从T[1]开始;
void get_next(String T, int next[]){
int i,j;
i=0;j=1;
next[1] = 0;
//abcdex
//遍历T模式串, 此时T[0]为模式串T的长度;
//printf("length = %d\n",T[0]);
while (j < T[0]) {
//T[i] 表示后缀的单个字符;
//T[j] 表示前缀的单个字符;
if (i == 0 || T[i] == T[j]) {
i++;j++;
next[j] = i;
}else{
//如果字符不相同,则i值回溯;
i = next[i];
}
}
}
3.4 KMP思路:
-
- 遍历模式串
S,i是用来标记主串的索引; 遍历模式串,j是用来标记模式串的索引;
- 遍历模式串
-
- 结束条件是当
i > S.length和j > T.length;如果i > S.length但是j却小于T.length表示遍历了整个主串,都没有找到与模式串匹配的情况,只有1种可能,就是j > T.length表示,已经在主串中找到模式串了. 因为你已经顺利的把T模式串中的每个字符串正常的依次比较下去了,直到它结束;
- 结束条件是当
-
- 当
j = 0时,表示此时你需要将模式串从1这个位置与主串i+1这个位置开始比较;
- 当
-
- 当
T[i] == T[j], 表示此时当前模式串j与 主串i这个2个字符是相等,则j++,i++;
- 当
-
- 当
j != 0并且T[i] != T[j]时,表示此时需要移动模式串的j,那么我们让j = next[j]; 来节省重复的比较次数;
- 当
3.5 KMP代码实现
int count = 0;
int Index_KMP(String S, String T, int pos){
//i 是主串当前位置的下标准,j是模式串当前位置的下标准
int i = pos;
int j = 1;
//定义一个空的next数组;
int next[MAXSIZE];
//对T串进行分析,得到next数组;
get_next(T, next);
count = 0;
//注意: T[0] 和 S[0] 存储的是字符串T与字符串S的长度;
//若i小于S长度并且j小于T的长度是循环继续;
while (i <= S[0] && j <= T[0]) {
//如果两字母相等则继续,并且j++,i++
if(j == 0 || S[i] == T[j]){
i++;
j++;
}else{
//如果不匹配时,j回退到合适的位置,i值不变;
j = next[j];
}
}
if (j > T[0]) {
return i-T[0];
}else{
return -1;
}
}
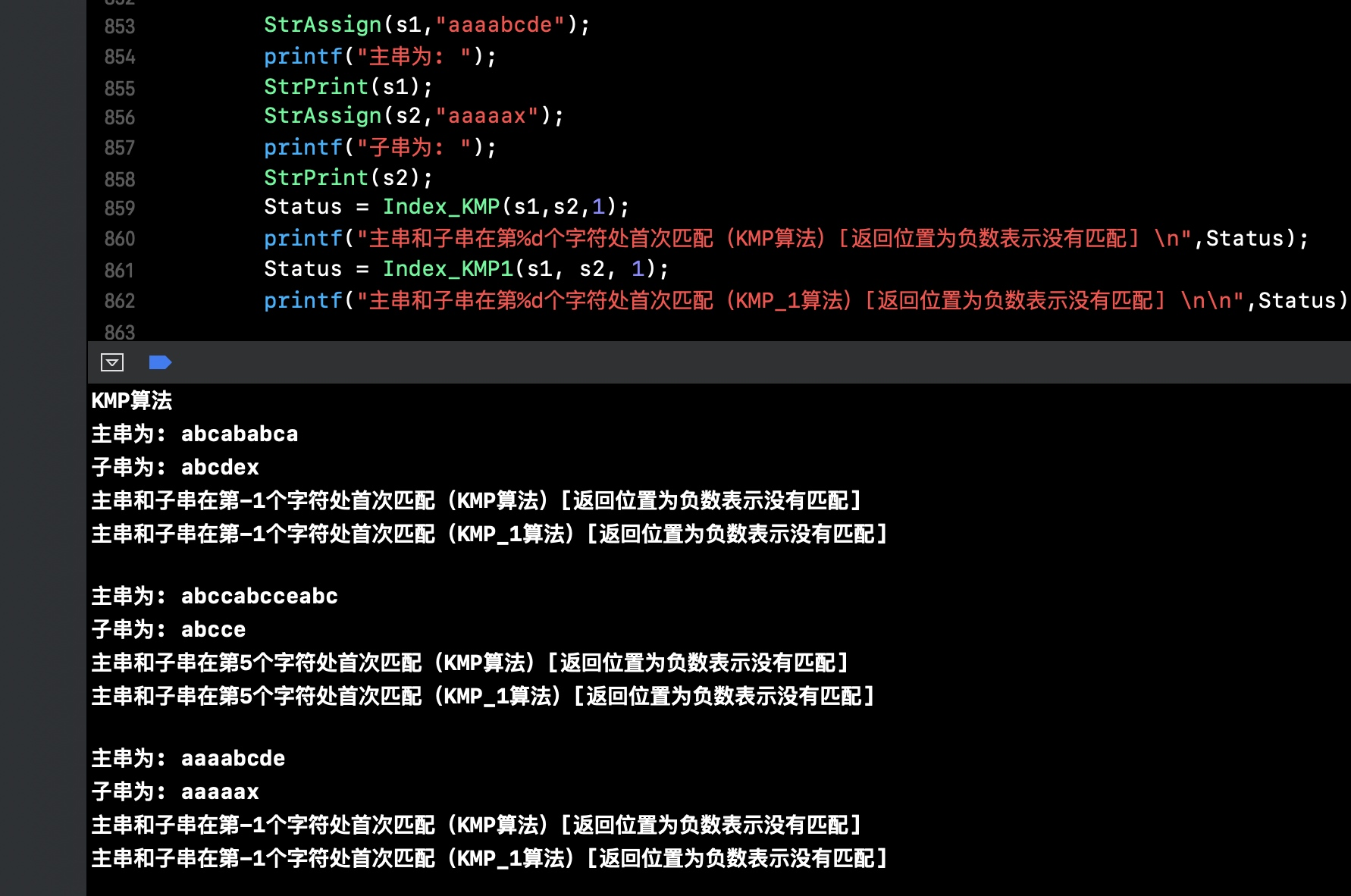
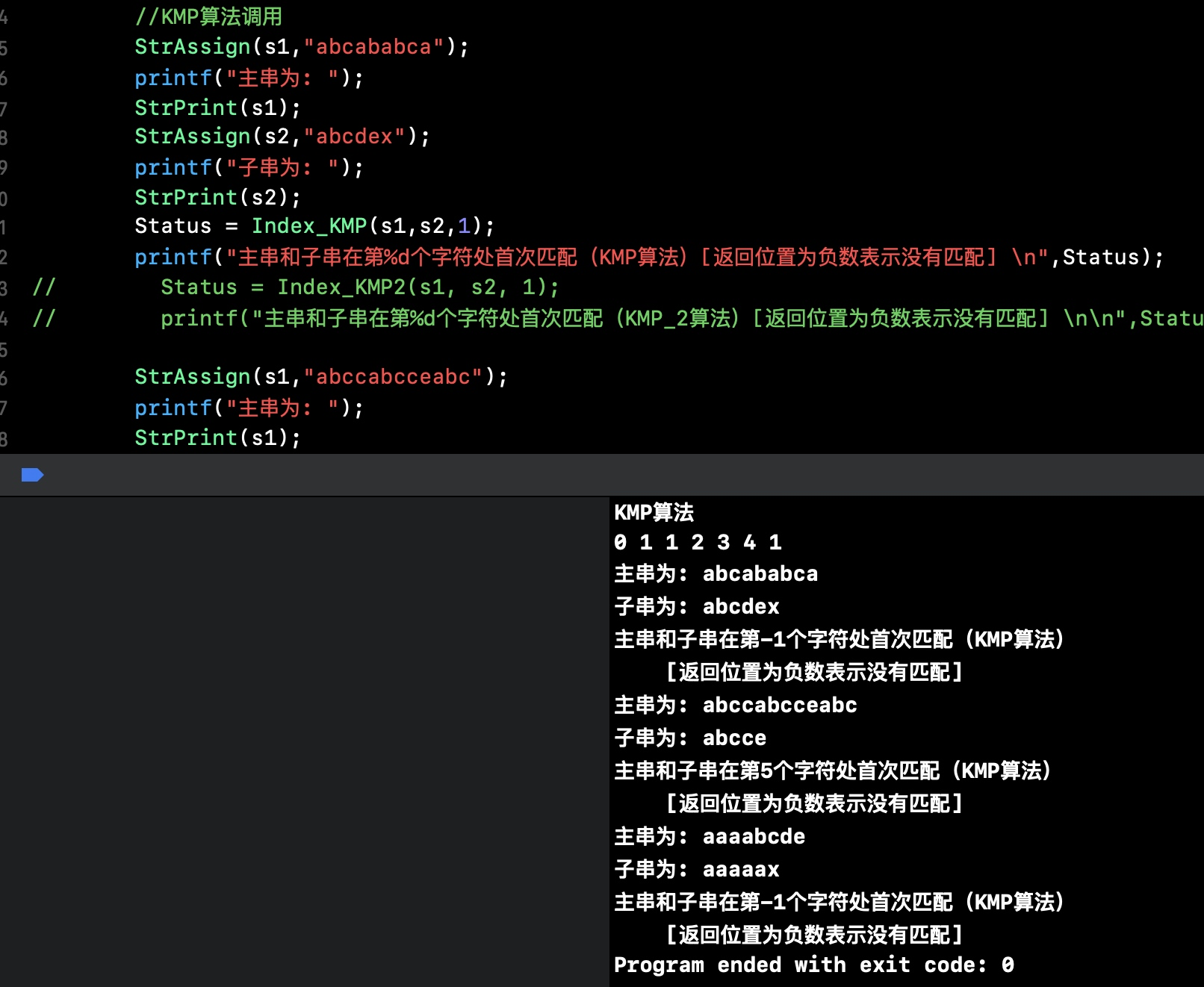
3.6 结果预期
4. KMP算法优化
假设, 主串S = “aaaabcde” ; 模式串 T = “aaaaax” 问题1: 此时模式串T 的next数组为{0,1,2,3,4,5}
问题:
那么当匹配到i=5,j=5时,匹配要逐步从j=4,3,2,1开始重新匹配,因为前面的字符串都相等,那么我们是否可以直接从j=1开始重新匹配.
4.1 next数组求解优化
这里我们举个例子 假设模式串T="ababaaaba"
j 123456789
T ababaaaba
next[j] 011234223
nextval[j] 010104210
解读:
- 当 j = 1, nextVal = 0;
- 当 j = 2, 因为第2个字符 “b” 的值next 值是1,而且第一个字符是”a”. 不相等. 所以 nextVal[2] = next[2] = 1;
- 当 j = 3, 因为第3个字符”a” 的next 值是1, 所以与第1位的”a”比较得知它们相等, 所以 nextval[3] = nextval[1] = 0;
- 当 j = 4, 因为第4个字符”b” 的next 值是2, 所以与第2位的”b”比较得知它们相等, 所以 nextval[4] = nextval[2] = 1;
- 当 j = 5 时,next 值为3 , 第5个字符”a” 与第3个字符”a” 相等,则nextVal[5] = nextVal[3] = 0;
- 当 j = 6 时,next 值为4 , 第6个字符”a” 与第4个字符”b” 不相等,则nextVal[6] = 4;
- 当 j = 7 时,next 值为2 , 第7个字符”a” 与第2个字符”b” 不相等,则nextVal[7] = 2;
- 当 j = 8 时,next 值为2 , 第8个字符”b” 与第2个字符”b” 相等,则nextVal[6] = nextVal[2] = 1;
- 当 j = 9 时, next 值为3, 第9个字符”a” 与第3个字符”a” 相等,则nextVal[9] = nextVal[3] = 0;
4.2 next优化总结
在求解nextVal数组的5种情况:
-
- 默认next[1] = 0;
-
- T[i] == T[j] 且++i,++j 后 T[i] 依旧等于 T[j] 则 nextval[i] = nextval[j];
-
- i = 0, 表示从头开始i++,j++后,且T[i] != T[j] 则nextVal = j;
-
- T[i] == T[j] 且++i,++j 后 T[i] != T[j] ,则nextVal = j;
-
- 当 T[i] != T[j]` 表示不相等,则需要将i 退回到合理的位置. 则 i = next[i];
4.3 next优化代码实现
void get_next1(String T, int nextval[]){
int i,j;
i=0;j=1;
nextval[1] = 0;
//abcdex
//遍历T模式串, 此时T[0]为模式串T的长度;
//printf("length = %d\n",T[0]);
while (j < T[0]) {
//T[i] 表示后缀的单个字符;
//T[j] 表示前缀的单个字符;
if (i == 0 || T[i] == T[j]) {
i++;j++;
//如果当前字符与前缀不同,则当前的j为nextVal 在i的位置的值
if (T[i] != T[j]) {
nextval[j] = i;
}else{
//如果当前字符与前缀相同,则将前缀的nextVal 值赋值给nextVal 在i的位置
nextval[j] = nextval[i];
}
}else{
//如果字符不相同,则i值回溯;
i = nextval[i];
}
}
}
4.4 KMP优化代码实现
int Index_KMP1(String S, String T, int pos){
//i 是主串当前位置的下标准,j是模式串当前位置的下标准
int i = pos;
int j = 1;
//定义一个空的next数组;
int next[MAXSIZE];
//对T串进行分析,得到next数组;
get_next1(T, next);
count = 0;
//注意: T[0] 和 S[0] 存储的是字符串T与字符串S的长度;
//若i小于S长度并且j小于T的长度是循环继续;
while (i <= S[0] && j <= T[0]) {
//如果两字母相等则继续,并且j++,i++
if(j == 0 || S[i] == T[j]){
i++;
j++;
}else{
//如果不匹配时,j回退到合适的位置,i值不变;
j = next[j];
}
}
if (j > T[0]) {
return i-T[0];
}else{
return -1;
}
}
4.5 结果预期