算法系列篇章-可以参照如下顺序阅读
1.数制转换(十进制转八进制)
1.1 思路分析
- 先将原数和要转换的进制数,进行求余,可以得到0位进制数值
- 再将原数除进制数,再求余可以得到第二位进制数
- 以此类推,可以将每个位数进制数压栈,由于栈的特性,先进后出,栈顶位置就是当前进制转换数的首位
- 然后将各个位置的进制数按照位置出栈,进行
10和栈长度计算,最终得到转换的进制数
1.2 代码实现
/* 数制转换 十进制转换为 8进制 2进制
numType 0是二进制 1是8进制 10以下进制转换
*/
int tenConvertToEight(int n, int numType){
int result = 0;
SqStack S;
// 当前要转换的数制
int type = numType == 0 ? 2 : 8;
// 初始化顺序栈
InitStack(&S);
while (n > 0){
int remainder = n % type;
// 将数据的每个数制位压栈
PushData(&S, remainder);
// 数制位左移
n = n / type;
}
int r = 0;
// 将每个数制位的值拼接为要转换的数制
while (S.top != -1) { // 当前栈顶位置不为空
// 出栈
Pop(&S, &result);
// 拼接
r += result * pow(10, StackLength(S));
}
return r;
}
1.3 结果预期
2.每日气温问题
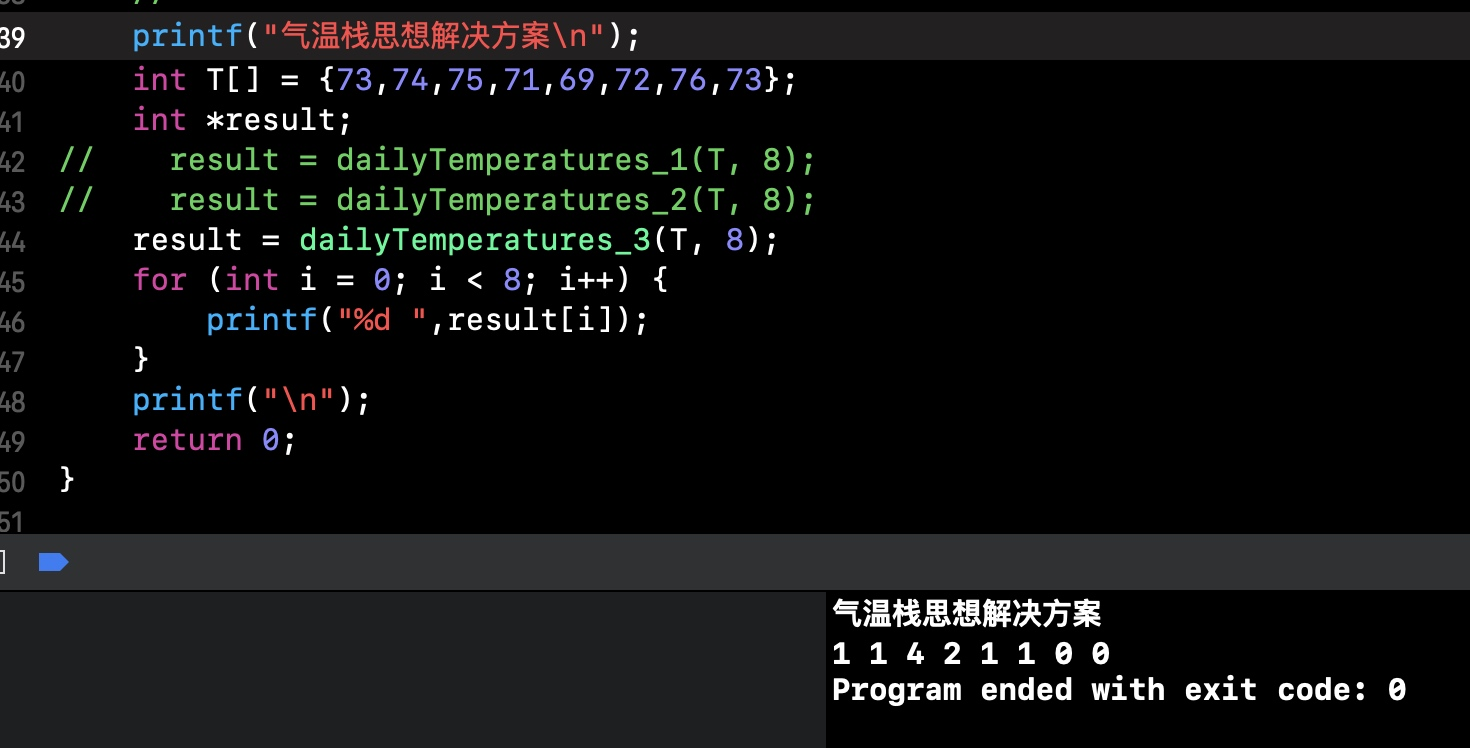
根据每⽇⽓温列表,请重新⽣生成⼀一个列表,对应位置的输入是你需要再等待多久温度才会升⾼超过该⽇日的天数。如果之后都不会升高,请在该位置0来代替。 例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73], 你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
提示:气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度,都是在 [30, 100] 范围内的整数。
2.1 问题分析
该问题的本质其实是查找从当前元素开始,往后要数多少次才能比当前位置i的温度要高,并且记录次数
2.2 解决方案
2.2.1 暴力法
1.思路分析
- 从左到右遍历,因为最后一个数没有后续元素,也就是气温不会再升高,所以默认为0
- 从第[i+1,Size]个数开始,直到找到比当前位置i温度高的元素的次数即为当前元素的值
2.代码实现
// 每日气温问题
// 暴力法
int *dailyTemperatures_1(int *T, int TSize){
// 初始化内存空间
int *result = malloc(sizeof(int) * TSize);
result[TSize-1] = 0; // 倒数第一个数没有后续,默认为0
// 从左到右遍历
for(int i = 0; i < TSize - 1; i++){
// 先解决后一个数和前一个数相等的情况,就不用循环直接赋值即可
if(i > 0 && T[i] == T[i-1]){
result[i] = (result[i - 1] == 0 ? 0 : (result[i-1] - 1));
}else{
for (int j = i + 1; j < TSize; j++) {
if (T[j] > T[i]) {
result[i] = j - i;
break;
}
// 处理倒数第二个小于等于倒数第一个的情况
if(j == TSize - 1){
result[i] = 0;
}
}
}
}
return result;
}
3.结果预期
2.2.2 跳跃对比(优化暴力法,减少遍历次数)
1.思路分析
- 从右到左遍历. 因为最后一天的气温不会再升高,默认等于0;
i从[TSize-2,0]; 从倒数第二天开始遍历比较. 每次减一;j从[i+1,TSize]遍历,j+=result[j],可以利用已经有结果的位置进行跳跃,从而减少遍历次数- 若
T[i]<T[j],那么Result = j - i; - 若
reuslt[j] == 0,则表示后面不会有更大的值,那么当前值就应该也是0;
- 若
2.代码实现
// 跳跃对比法
int *dailyTemperatures_2(int *T, int TSize){
// 初始化内存空间
int *result = malloc(sizeof(int) * TSize);
result[TSize-1] = 0; // 倒数第一个数没有后续,默认为0
for (int i = TSize - 2; i >= 0; i--) {
// 从i+1 -> TSize - 1遍历处理
for (int j = i+1; j < TSize; j++) {
if(T[i] < T[j]){
result[i] = j - i;
break;
}else{
if (result[j] == 0) { //如果后面没有更大的值代表当前值也为0
result[i] = 0;
break;
}
}
}
}
return result;
}
3.结果预期
2.2.3 利用栈思想解决
1.思路分析
- 初始化一个栈(用来存储索引)
value数组 - 栈中存储的是元素的索引值
index; - 遍历整个温度数组从
[0,TSize];- (1).如果栈顶元素<当前元素,则将当前元素索引
index-栈顶元素index,计算完毕则将当前栈顶元素移除,将当前元素索引index存储到栈中; 出栈后,只要栈不为空.继续比较,直到栈顶元素不能满足T[i] > T[stack_index[top-1]] - (2).如果当前的栈为空,则直接入栈;
- (3).如果当前的元素小于栈顶元素,则入栈
- (4).
if循环结束后,当前元素也需要入栈;
- (1).如果栈顶元素<当前元素,则将当前元素索引
2.代码实现
// 跳跃对比法
int *dailyTemperatures_3(int *T, int TSize){
// 初始化内存空间
int *result = malloc(sizeof(int) * TSize);
// 初始化栈空间
int *stack = malloc(sizeof(int) * TSize);
int top = 0; // 栈顶指针
int tIndex; // 栈元素位置标记
for (int i = 0; i < TSize; i++) {
result[i] = 0;
// 栈不是空栈 以及当前元素大于栈顶元素值
while (top > 0 && T[i] > T[stack[top - 1]]) {
tIndex = stack[top - 1];
result[tIndex] = i - tIndex;
top--;
}
// 当前元素小于栈顶元素 入栈 或者空栈直接入栈
stack[top] = i;
top++;
}
return result;
}
3.结果预期
3.杨辉三角
给定一个非负整数numRows生成杨辉三角的前 numRows行,如下图:
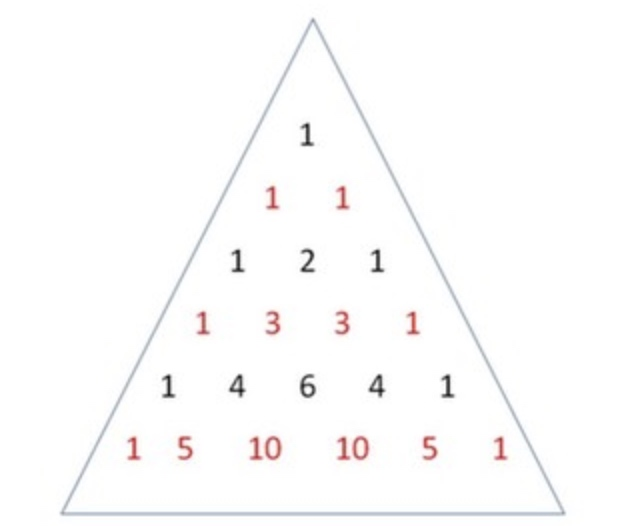
3.1 思路分析
- 第一层循环控制行数i : 默认
[i][0] = 1,[i][i] = 1; - 第二层循环控制列数j :
triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j];
3.2 代码实现
// 杨辉三角问题
int **generate(int numRows){
int **res = (int **)malloc(sizeof(int *)*numRows);
for (int i = 0; i < numRows; i++) {
// 每一行显示的数组
res[i] = (int *)malloc(sizeof(int*)*(i+1));
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i) { // 每行第一个和最后一个数字都是1
res[i][j] = 1;
}else{
res[i][j] = res[i - 1][j] + res[i-1][j-1];
}
}
}
return res;
}
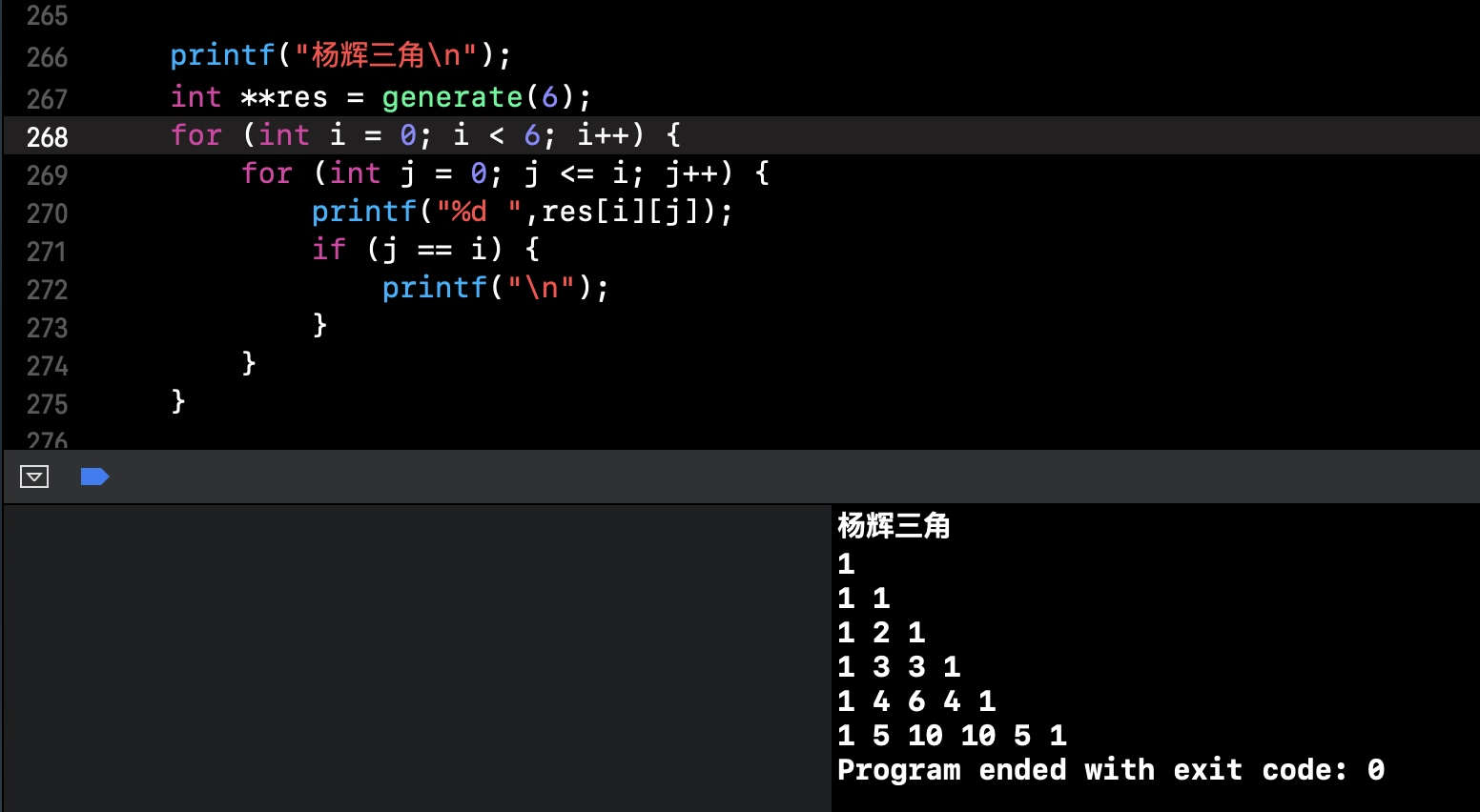
3.3 结果预期
4.爬楼梯问题
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? **注意:**给定 n 是一个正整数。
4.1 思路分析
- 如题干所述,可以分解下,如果
n=2, 就有两种情况,1+1或者2,两种解法 - 如果
n=3,就有如下三种种情况1+1+1,1+2,2+1 - 第一种解法:很容易判断可以使用递归,简单理解就是把爬一个台阶的情况和爬两个台阶的情况加起来
- 第二种解法,不难发现,这个问题可以被分解为一些包含最优子结构的子问题,即它的最优解可以从其子问题的最优解来有效地构建,我们可以使用动态规划来解决这一问题。
- 第
i阶可以由以下两种方法得到:在第(i−1)阶后向上爬一阶。在第(i−2)阶后向上爬二阶。 - 所以到达第
i阶的方法总数就是到第(i−1)阶和第(i−2)阶的方法数之和。
- 第
4.2 递归法代码实现
// 爬楼梯问题递归法
int floorWay(int n){
if (n == 0) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
return floorWay(n-1) + floorWay(n-2);
}
4.3 动态规划法代码实现
int clipFloor(int n){
if (n == 1) return 1;
int *res = (int *)malloc(sizeof(int)*(n+1));
res[0] = 0;
res[1] = 1;
res[2] = 2;
for (int i = 3; i <= n; i++) {
res[i] = res[i-1] + res[i-2];
}
return res[n];
}
4.4 结果预期