[ CodeWar ] - 014：解析公有质因虽然上述代码已经解决了问题，但思路挺傻的，这里我们看看应该怎么进行优化。

系列文章

题目

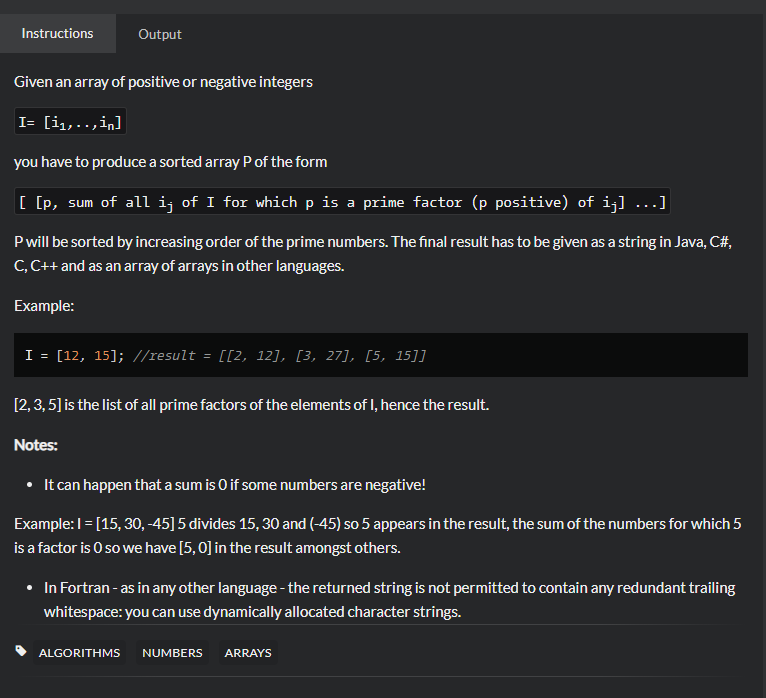
需求：

输入是一个全是整数的列表
需要找到它们的质因数，以从小到大的顺序排列
并且每个质因素，要算出它所对应的合数集合的总和

解析

这道题乍一看挺唬人的，不过实际上要比解析化学式那道简单许多，至少思路比较直接：

step 1：计算出每个整数的所有质因并去重
step 2：合并所有质因并去重
step 3：遍历得到的质因数集合，将拥有相同质因数的整数放进同一组
step 4：计算每一组整数的和
step 5：将质因数集合与和的集合排序后合并成返回的格式

const getPrimeFactor = (num) => {
  num = Math.abs(num)
  let i = 2,
    ret = [],
    loop = num - i + 1

  while (loop--) {
    while (num % i === 0) {
      num /= i
      ret.push(i)
    }
    i++
  }

  return [...new Set(ret)]
}

function sumOfDivided(lst) {
  if (lst.length === 0) return []
  let allPrimeFactor = [...new Set(lst.map((num) => getPrimeFactor(num)).reduce((pre, cur) => [...pre, ...cur]))].sort(
    (a, b) => a - b
  )
  let allSum = allPrimeFactor
    .map((p) => {
      let ret = []
      lst.forEach((num) => {
        if (num % p === 0) {
          ret.push(num)
        }
      })
      return ret
    })
    .map((cl) => cl.reduce((pre, cur) => pre + cur, 0))

  return allPrimeFactor.map((p, i) => [p, allSum[i]])
}

优化

虽然上述代码已经解决了问题，但思路挺傻的，这里我们看看应该怎么进行优化。

这里我们先声明几个数组：

i：输入的数组

p：用于存储小于 max 的所有质数

s：用于存储拥有相同质因的数

o：输出的数组

首先我们可以找出输入列表的最大值，在一次循环中依次处理每个数
当循环开始的时候，首先判断 p 中有没有能够整除 i 的数，如果有则说明 i 是质数
接下来先将 i 加进 p，然后遍历 i，看是否有数能够被 i 整除，如果有则说明 i 是其质因，将这个数加入 s
当 s 的长度不为 0 的时候则说明存在能被 i 整除的数，计算 s 的总和，并且与 i 一组加入 o 中
最后返回 o

const sumOfDivided = (lst, max = Math.max(...lst.map(Math.abs)), pris = [], sums = [], rets = []) => {
  for (i = 2; i <= max; ++i) {
    pris.some((p) => i % p === 0) ||
      (pris.push(i) && (sums = lst.filter((n) => n % i === 0)).length && rets.push([i, sums.reduce((a, b) => a + b)]))
  }
  return rets
}