Python 机器学习示例(二)
五、使用逻辑回归预测在线广告点击率
在前一章中,我们使用树算法预测了广告点击率。在这一章中,我们将继续我们解决十亿美元问题的旅程。我们将集中学习一个非常(可能是最)可扩展的分类模型——逻辑回归。我们将探讨什么是逻辑回归函数,如何训练逻辑回归模型,向模型添加正则化,以及适用于非常大数据集的逻辑回归变体。除了在分类中的应用,我们还将讨论如何使用逻辑回归和随机森林来挑选重要特征。您不会感到厌烦,因为 scikit-learn 和 TensorFlow 将有许多从头开始的实现。
在本章中,我们将涵盖以下主题:
- 分类特征编码
- 逻辑函数
- 什么是逻辑回归?
- 梯度下降和随机梯度下降
- 逻辑回归的实现
- 逻辑回归点击率预测
- L1 和 L2 正则化的逻辑回归
- 特征选择的逻辑回归
- 在线学习
- 选择要素的另一种方式——随机森林
将分类特征转换为数字-一热编码和序数编码
在第 4 章、用基于树的算法预测在线广告点击率中,我提到了一键编码如何将分类特征转换为数字特征,以便在 scikit-learn 和 TensorFlow 中的树算法中使用它们。如果我们使用一次性编码将分类特征转换为数字特征,我们不会将算法的选择局限于能够处理分类特征的基于树的算法。
在将分类特征转换为 k 可能值方面,我们能想到的最简单的解决方案是将其映射为数值从 1 到 k 的数字特征。例如,[Tech,Fashion,Fashion,Sports,Tech,Tech,Sports]变成[1,2,2,3,1,1,3]。然而,这将强加一个序数特征,例如体育大于科技,以及一个距离属性,例如体育更接近时尚而不是科技。
相反,一键编码将分类特征转换为 k 二进制特征。每个二进制特征指示对应的可能值的存在或不存在。因此,前面的例子变成了下面的例子:
图 5.1:通过一键编码将用户兴趣转化为数字特征
之前我们使用过 scikit-learn 中的OneHotEncoder将一个字符串矩阵转换成二进制矩阵,但是在这里,我们再来看看另一个模块DictVectorizer,它也提供了一个高效的转换。它将字典对象(分类特征:值)转换成单热编码向量。
例如,看看下面的代码:
>>> from sklearn.feature_extraction import DictVectorizer
>>> X_dict = [{'interest': 'tech', 'occupation': 'professional'},
... {'interest': 'fashion', 'occupation': 'student'},
... {'interest': 'fashion','occupation':'professional'},
... {'interest': 'sports', 'occupation': 'student'},
... {'interest': 'tech', 'occupation': 'student'},
... {'interest': 'tech', 'occupation': 'retired'},
... {'interest': 'sports','occupation': 'professional'}]
>>> dict_one_hot_encoder = DictVectorizer(sparse=False)
>>> X_encoded = dict_one_hot_encoder.fit_transform(X_dict)
>>> print(X_encoded)
[[ 0\. 0\. 1\. 1\. 0\. 0.]
[ 1\. 0\. 0\. 0\. 0\. 1.]
[ 1\. 0\. 0\. 1\. 0\. 0.]
[ 0\. 1\. 0\. 0\. 0\. 1.]
[ 0\. 0\. 1\. 0\. 0\. 1.]
[ 0\. 0\. 1\. 0\. 1\. 0.]
[ 0\. 1\. 0\. 1\. 0\. 0.]]
我们也可以通过执行以下操作来查看映射:
>>> print(dict_one_hot_encoder.vocabulary_)
{'interest=fashion': 0, 'interest=sports': 1,
'occupation=professional': 3, 'interest=tech': 2,
'occupation=retired': 4, 'occupation=student': 5}
谈到新数据,我们可以通过以下方式进行转换:
>>> new_dict = [{'interest': 'sports', 'occupation': 'retired'}]
>>> new_encoded = dict_one_hot_encoder.transform(new_dict)
>>> print(new_encoded)
[[ 0\. 1\. 0\. 0\. 1\. 0.]]
我们可以将编码后的特征反向转换回原始特征,如下所示:
>>> print(dict_one_hot_encoder.inverse_transform(new_encoded))
[{'interest=sports': 1.0, 'occupation=retired': 1.0}]
需要注意的一点是,如果在新数据中遇到新的(在训练数据中没有看到的)类别,则应该忽略它(否则,编码器会抱怨看不见的类别值)。DictVectorizer隐式处理(而OneHotEncoder需要指定参数ignore):
>>> new_dict = [{'interest': 'unknown_interest',
'occupation': 'retired'},
... {'interest': 'tech', 'occupation':
'unseen_occupation'}]
>>> new_encoded = dict_one_hot_encoder.transform(new_dict)
>>> print(new_encoded)
[[ 0\. 0\. 0\. 0\. 1\. 0.]
[ 0\. 0\. 1\. 0\. 0\. 0.]]
有时,我们更喜欢将具有 k 可能值的分类特征转换为数值范围从 1 到 k 的数值特征。我们进行序数编码,以便在我们的学习中使用序数或排序知识;例如,大、中和小分别变成 3、2 和 1;好的和坏的变成 1 和 0,而一热编码不能保存这些有用的信息。我们可以通过pandas的使用轻松实现序数编码,例如:
>>> import pandas as pd
>>> df = pd.DataFrame({'score': ['low',
... 'high',
... 'medium',
... 'medium',
... 'low']})
>>> print(df)
score
0 low
1 high
2 medium
3 medium
4 low
>>> mapping = {'low':1, 'medium':2, 'high':3}
>>> df['score'] = df['score'].replace(mapping)
>>> print(df)
score
0 1
1 3
2 2
3 2
4 1
我们根据我们定义的映射将字符串特征转换为序数值。
我们已经讨论了将分类特征转换成数字特征。接下来,我们将讨论逻辑回归,一个只接受数字特征的分类器。
用逻辑回归对数据进行分类
在最后一章中,我们只基于 4000 万个样本中的前 30 万个样本来训练基于树的模型。我们这样做只是因为在一个大数据集上训练一棵树在计算上非常昂贵和耗时。由于一热编码,我们现在不局限于直接采用分类特征的算法,我们应该转向一种对大型数据集具有高度可扩展性的新算法。如上所述,逻辑回归是最,或者可能是最可扩展的分类算法之一。
开始使用物流功能
在我们深入研究算法本身之前,让我们首先介绍一下作为算法核心的逻辑函数(更常见的说法是为 sigmoid 函数)。它基本上将输入映射为 0 和 1 之间的值的输出,定义如下:
我们可以通过执行以下步骤来可视化它的外观:
-
定义物流函数:
>>> import numpy as np >>> def sigmoid(input): ... return 1.0 / (1 + np.exp(-input)) -
输入变量从-
8到8,以及相应的输出,如下:>>> z = np.linspace(-8, 8, 1000) >>> y = sigmoid(z) >>> import matplotlib.pyplot as plt >>> plt.plot(z, y) >>> plt.axhline(y=0, ls='dotted', color='k') >>> plt.axhline(y=0.5, ls='dotted', color='k') >>> plt.axhline(y=1, ls='dotted', color='k') >>> plt.yticks([0.0, 0.25, 0.5, 0.75, 1.0]) >>> plt.xlabel('z') >>> plt.ylabel('y(z)') >>> plt.show()
最终结果参见下面的截图:
图 5.2:逻辑功能
在 S 形曲线中,所有输入都被转换到 0 到 1 的范围内。对于正输入,值越大,输出越接近 1;对于负输入,较小的值产生接近 0 的输出;当输入为 0 时,输出为中点 0.5。
从逻辑函数到逻辑回归的跳跃
现在您已经了解了逻辑函数,很容易将其映射到源自该函数的算法。在逻辑回归中,函数输入 z 变成特征的加权和。给定一个带有 n 特征的数据样本 x ,xT10】1T12】,xT14】2T16,…,xT18】n(x代表一个特征向量,并且x =(xT24】1T26】,xT28】2T32 以及型号 w ( w 代表矢量*(w*T47】1T49,wT51】2T53,…,wT55】nT57)】z【T69】
此外,偶尔,模型附带一个截距(也称为偏差), w 0 。在这种情况下,前面的线性关系变为:
对于 0 到 1 范围内的输出 y(z) ,在算法中变成目标为 1 或正类的概率:
因此,逻辑回归是一个概率分类器,类似于朴素贝叶斯分类器。
从训练数据中学习逻辑回归模型,或者更具体地说,其权重向量 w ,目标是预测尽可能接近于 1 的正样本,并预测尽可能接近于 0 的负样本。在数学语言中,训练权重以使定义为均方误差 ( 均方误差)的成本最小化,其中测量真实值和预测值之间差值的平方平均值。给定 m 个训练样本,、
、…
……、
,其中 y (i) 为 1 (正类)或 0 (负类)成本函数 J(w) 关于待优化权重表示如下:
然而,前面的代价函数是非凸的,这意味着在搜索最优 w 时,发现了许多局部(次优)最优,并且函数没有收敛到全局最优。
下面分别绘制了凸和非凸函数的示例:
图 5.3:凸函数和非凸函数的例子
在凸的例子中,只有一个全局最优,而在非凸的例子中有两个最优。关于凸函数和非凸函数的更多信息,请随时查看en.wikipedia.org/wiki/Convex…和https://web . Stanford . edu/class/ee 364 a/讲座/函数. pdf 。
为了克服这一点,实际中的成本函数定义如下:
我们可以仔细看看单个培训样本的成本:
当地面真相 y (i) = 1 时,如果模型完全可信地预测正确(概率为 100%的正类),则样本成本 j 为0;当预测概率降低时,成本 j 增加。如果模型错误地预测没有正类的机会,那么成本是无限高的。我们可以将其可视化如下:
>>> y_hat = np.linspace(0, 1, 1000)
>>> cost = -np.log(y_hat)
>>> plt.plot(y_hat, cost)
>>> plt.xlabel('Prediction')
>>> plt.ylabel('Cost')
>>> plt.xlim(0, 1)
>>> plt.ylim(0, 7)
>>> plt.show()
有关最终结果,请参考下图:
图 5.4:y = 1 时逻辑回归的成本函数
相反,当地面真值 y (i) = 0 时,如果模型完全可信地正确预测(概率为 0 的正类,或概率为 100%的负类),则样本成本 j 为0;当预测概率增加时,成本 j 增加。当它错误地预测没有负类的机会时,成本变得无限高。我们可以使用以下代码将其可视化:
>>> y_hat = np.linspace(0, 1, 1000)
>>> cost = -np.log(1 - y_hat)
>>> plt.plot(y_hat, cost)
>>> plt.xlabel('Prediction')
>>> plt.ylabel('Cost')
>>> plt.xlim(0, 1)
>>> plt.ylim(0, 7)
>>> plt.show()
下图是结果输出:
图 5.5:y = 0 时逻辑回归的成本函数
最小化这个替代成本函数实际上相当于最小化基于 MSE 的成本函数。选择它比选择 MSE 的优势包括以下几点:
- 显然,是凸的,这样可以找到最佳的模型权重
- 预测的对数的总和
或
简化了其相对于权重的导数的计算,这将在后面讨论
由于对数函数,成本函数也称为对数损失,或简称对数损失。
既然我们已经准备好了成本函数,我们如何训练逻辑回归模型来最小化成本函数?让我们在下一节看到。
训练逻辑回归模型
现在的问题是我们如何获得最优的 w 使得 J(w) 最小化。我们可以使用梯度下降来做到这一点。
使用梯度下降训练逻辑回归模型
梯度下降(也称为最速下降)是通过一阶迭代优化最小化目标函数的过程。在每次迭代中,它在当前点移动一个与目标函数的负导数成比例的步长。这意味着待优化点朝着目标函数的最小值迭代地向下移动。我们刚才提到的比例是称为学习率,或者步长。它可以用一个数学方程式概括如下:
这里左边的 w 是学习一步后的权重向量,右边的 w 是移动前的权重向量, η 是学习率,∮w是一阶导数,梯度。
在我们的例子中,让我们从成本函数 J(w) 相对于 w 的导数开始。这可能需要一些微积分的知识,但是不要担心,我们会一步一步地完成它:
-
我们首先计算
相对于 w 的导数。我们这里以 j-th 权重, w j 为例(注z = wTx,为简单起见省略(I):
-
然后,我们计算样本成本的导数 J(w) 如下:
-
最后,我们计算整个成本超过 m 样品如下:
-
然后我们将其概括为∮w:
-
Combined with the preceding derivations, the weights can be updated as follows:
这里, w 在每次迭代中更新。
-
经过大量迭代后,所学习的 w 和 b 然后被用于通过以下等式对新样本 x 进行分类:
决策阈值默认为 0.5,但肯定可以是其他值。在无论如何都应该避免假阴性的情况下,例如,当预测警报的火灾发生(阳性类别)时,决策阈值可以低于 0.5,例如 0.3,这取决于我们有多偏执以及我们想要多主动地防止阳性事件发生。另一方面,当假阳性类别是应该回避的类别时,例如,当预测质量保证的产品成功率(阳性类别)时,决策阈值可以大于 0.5,例如 0.7,或者小于 0.5,这取决于您设置的标准有多高。
彻底了解基于梯度下降的训练和预测过程后,我们现在将从头开始实施逻辑回归算法:
-
我们首先定义用当前权重计算预测的函数【T1:
>>> def compute_prediction(X, weights): ... """ ... Compute the prediction y_hat based on current weights ... """ ... z = np.dot(X, weights) ... predictions = sigmoid(z) ... return predictions -
这样,我们就能够以梯度下降的方式一步一步地继续更新权重
的功能。看看下面的代码:
>>> def update_weights_gd(X_train, y_train, weights, learning_rate): ... """ ... Update weights by one step ... """ ... predictions = compute_prediction(X_train, weights) ... weights_delta = np.dot(X_train.T, y_train - predictions) ... m = y_train.shape[0] ... weights += learning_rate / float(m) * weights_delta ... return weights -
然后,计算成本 J(w) 的功能也被实现:
>>> def compute_cost(X, y, weights): ... """ ... Compute the cost J(w) ... """ ... predictions = compute_prediction(X, weights) ... cost = np.mean(-y * np.log(predictions) - (1 - y) * np.log(1 - predictions)) ... return cost -
Now, we connect all these functions to the model training function by executing the following:
- 在每次迭代中更新
weights向量 - 打印出每一次
100(这可以是另一个值)迭代的当前成本,以确保cost正在减少,并且事情在正确的轨道上
它们在以下功能中实现:
>>> def train_logistic_regression(X_train, y_train, max_iter, learning_rate, fit_intercept=False): ... """ Train a logistic regression model ... Args: ... X_train, y_train (numpy.ndarray, training data set) ... max_iter (int, number of iterations) ... learning_rate (float) ... fit_intercept (bool, with an intercept w0 or not) ... Returns: ... numpy.ndarray, learned weights ... """ ... if fit_intercept: ... intercept = np.ones((X_train.shape[0], 1)) ... X_train = np.hstack((intercept, X_train)) ... weights = np.zeros(X_train.shape[1]) ... for iteration in range(max_iter): ... weights = update_weights_gd(X_train, y_train, weights, learning_rate) ... # Check the cost for every 100 (for example) iterations ... if iteration % 100 == 0: ... print(compute_cost(X_train, y_train, weights)) ... return weights - 在每次迭代中更新
-
最后,我们使用训练好的模型预测新输入的结果如下:
>>> def predict(X, weights): ... if X.shape[1] == weights.shape[0] - 1: ... intercept = np.ones((X.shape[0], 1)) ... X = np.hstack((intercept, X)) ... return compute_prediction(X, weights)
正如您刚刚看到的,实现逻辑回归非常简单。现在让我们用一个玩具例子来检验它:
>>> X_train = np.array([[6, 7],
... [2, 4],
... [3, 6],
... [4, 7],
... [1, 6],
... [5, 2],
... [2, 0],
... [6, 3],
... [4, 1],
... [7, 2]])
>>> y_train = np.array([0,
... 0,
... 0,
... 0,
... 0,
... 1,
... 1,
... 1,
... 1,
... 1])
我们为1000 迭代训练逻辑回归模型,在基于包含截距的权重训练0.1的学习率:
>>> weights = train_logistic_regression(X_train, y_train,
max_iter=1000, learning_rate=0.1, fit_intercept=True)
0.574404237166
0.0344602233925
0.0182655727085
0.012493458388
0.00951532913855
0.00769338806065
0.00646209433351
0.00557351184683
0.00490163225453
0.00437556774067
成本的降低意味着模型会随着时间的推移而优化。我们可以在新样本上检查模型的性能,如下所示:
>>> X_test = np.array([[6, 1],
... [1, 3],
... [3, 1],
... [4, 5]])
>>> predictions = predict(X_test, weights)
>>> predictions
array([ 0.9999478 , 0.00743991, 0.9808652 , 0.02080847])
要可视化这一点,请执行以下代码:
>>> import matplotlib.pyplot as plt
>>> plt.scatter(X_train[:,0], X_train[:,1], c=['b']*5+['k']*5,
marker='o')
蓝色点是 0 班的训练样本,黑色点是 1 班的。使用0.5作为分类决策阈值:
>>> colours = ['k' if prediction >= 0.5 else 'b'
for prediction in predictions]
>>> plt.scatter(X_test[:,0], X_test[:,1], marker='*', c=colours)
蓝星是测试从 0 级预测的样本,而黑星是从 1 级预测的样本:
>>> plt.xlabel('x1')
>>> plt.ylabel('x2')
>>> plt.show()
有关最终结果,请参考以下屏幕截图:
图 5.6:玩具示例的训练和测试集
我们训练的模型正确预测了新样本(恒星)的类。
梯度下降逻辑回归预测广告点击率
在这个简短的例子之后,我们将现在部署我们刚刚在点进预测项目中开发的算法。
我们在此仅从 10,000 个训练样本开始(您很快就会明白为什么我们不像上一章那样从 270,000 个样本开始):
>>> import pandas as pd
>>> n_rows = 300000
>>> df = pd.read_csv("train", nrows=n_rows)
>>> X = df.drop(['click', 'id', 'hour', 'device_id', 'device_ip'],
axis=1).values
>>> Y = df['click'].values
>>> n_train = 10000
>>> X_train = X[:n_train]
>>> Y_train = Y[:n_train]
>>> X_test = X[n_train:]
>>> Y_test = Y[n_train:]
>>> from sklearn.preprocessing import OneHotEncoder
>>> enc = OneHotEncoder(handle_unknown='ignore')
>>> X_train_enc = enc.fit_transform(X_train)
>>> X_test_enc = enc.transform(X_test)
以带有偏差的0.01的学习率,在10000迭代上训练逻辑回归模型:
>>> import timeit
>>> start_time = timeit.default_timer()
>>> weights = train_logistic_regression(X_train_enc.toarray(),
Y_train, max_iter=10000, learning_rate=0.01,
fit_intercept=True)
0.6820019456743648
0.4608619713011896
0.4503715555130051
…
…
…
0.41485094023829017
0.41477416506724385
0.41469802145452467
>>> print(f"--- {(timeit.default_timer() - start_time)}.3fs seconds ---")
--- 232.756s seconds ---
需要232 seconds对模型进行优化。训练好的模型在测试集上的表现如下:
>>> pred = predict(X_test_enc.toarray(), weights)
>>> from sklearn.metrics import roc_auc_score
>>> print(f'Training samples: {n_train}, AUC on testing set: {roc_auc_score(Y_test, pred):.3f}')
Training samples: 10000, AUC on testing set: 0.703
现在,让我们使用 10 万个训练样本(n_train = 100000)重复同样的过程。用时 5240.4 秒,差不多 1.5 小时。容纳 10 倍大小的数据需要 22 倍的时间。正如我在本章开头提到的,逻辑回归分类器在大数据集上的训练非常好。但是我们的检测结果似乎与此相矛盾。我们如何高效地处理更大的训练数据集,不仅仅是 10 万个样本,而是数百万个样本?在下一节中,让我们看看训练逻辑回归模型的更有效的方法。
使用随机梯度下降训练逻辑回归模型
在基于梯度下降的逻辑回归模型中,所有训练样本用于在每次迭代中更新权重。因此,如果训练样本的数量很大,整个训练过程将变得非常耗时,并且计算成本很高,正如您刚刚在我们的最后一个示例中看到的那样。
幸运的是,一个小小的调整将使逻辑回归适合大规模数据集。每次权重更新,只消耗一个训练样本,而不是完整的训练集。该模型基于单个训练样本计算的误差移动一步。一旦使用了所有样本,一次迭代就结束了。这个梯度下降的高级版本被称为随机梯度下降 ( SGD )。用公式表示,对于每次迭代,我们执行以下操作:
SGD 通常比梯度下降收敛得更快,梯度下降通常需要大量的迭代。
为了实现基于 SGD 的逻辑回归,我们只需要稍微修改一下update_weights_gd函数:
>>> def update_weights_sgd(X_train, y_train, weights,
learning_rate):
... """ One weight update iteration: moving weights by one
step based on each individual sample
... Args:
... X_train, y_train (numpy.ndarray, training data set)
... weights (numpy.ndarray)
... learning_rate (float)
... Returns:
... numpy.ndarray, updated weights
... """
... for X_each, y_each in zip(X_train, y_train):
... prediction = compute_prediction(X_each, weights)
... weights_delta = X_each.T * (y_each - prediction)
... weights += learning_rate * weights_delta
... return weights
在train_logistic_regression功能中,应用 SGD:
>>> def train_logistic_regression_sgd(X_train, y_train, max_iter,
learning_rate, fit_intercept=False):
... """ Train a logistic regression model via SGD
... Args:
... X_train, y_train (numpy.ndarray, training data set)
... max_iter (int, number of iterations)
... learning_rate (float)
... fit_intercept (bool, with an intercept w0 or not)
... Returns:
... numpy.ndarray, learned weights
... """
... if fit_intercept:
... intercept = np.ones((X_train.shape[0], 1))
... X_train = np.hstack((intercept, X_train))
... weights = np.zeros(X_train.shape[1])
... for iteration in range(max_iter):
... weights = update_weights_sgd(X_train, y_train, weights,
learning_rate)
... # Check the cost for every 2 (for example) iterations
... if iteration % 2 == 0:
... print(compute_cost(X_train, y_train, weights))
... return weights
现在,让我们来看看 SGD 有多强大。我们将处理 10 万个训练样本,选择10作为迭代次数,0.01作为作为学习率,每隔一次迭代打印出当前成本:
>>> start_time = timeit.default_timer()
>>> weights = train_logistic_regression_sgd(X_train_enc.toarray(),
Y_train, max_iter=10, learning_rate=0.01, fit_intercept=True)
0.4127864859625796
0.4078504597223988
0.40545733114863264
0.403811787845451
0.4025431351250833
>>> print(f"--- {(timeit.default_timer() - start_time)}.3fs seconds ---")
--- 40.690s seconds ---
>>> pred = predict(X_test_enc.toarray(), weights)
>>> print(f'Training samples: {n_train}, AUC on testing set: {roc_auc_score(Y_test, pred):.3f}')
Training samples: 100000, AUC on testing set: 0.732
训练过程只需 40 秒就结束了!
像往常一样,在从头开始成功实现基于 SGD 的逻辑回归算法之后,我们使用 scikit-learn 的SGDClassifier模块来实现它:
>>> from sklearn.linear_model import SGDClassifier
>>> sgd_lr = SGDClassifier(loss='log', penalty=None,
fit_intercept=True, max_iter=10,
learning_rate='constant', eta0=0.01)
这里,loss参数的'log'表示代价函数是对数损失,penalty是减少过拟合的正则化项,我们将在下一节中进一步讨论,max_iter是迭代次数,其余两个参数表示学习率为0.01,在训练过程中不变。需要注意的是,默认learning_rate为'optimal',随着更新越来越多,学习率略有下降。这有利于在大型数据集上找到最优解。
现在,训练模型并测试它:
>>> sgd_lr.fit(X_train_enc.toarray(), Y_train)
>>> pred = sgd_lr.predict_proba(X_test_enc.toarray())[:, 1]
>>> print(f'Training samples: {n_train}, AUC on testing set: {roc_auc_score(Y_test, pred):.3f}')
Training samples: 100000, AUC on testing set: 0.734
又快又容易!
正则化训练逻辑回归模型
正如我在前面的部分简要提到的,逻辑回归SGDClassifier中的penalty参数与模型正则化相关。正规化有和两种基本形式, L1 (也叫套索)和 L2 (也叫脊)。无论采用哪种方式,正则化都是原始成本函数之上的附加项:
这里, α 是乘以正则化项的常数, q 是代表 L1 或 L2 正则化的 1 或 2 ,适用于以下情况:
训练逻辑回归模型是将成本降低为权重的函数的过程。如果到了某些权重,比如wIwjwk相当大的时候,整个成本就由这些大权重决定了。在这种情况下,学习的模型可能只是记住了训练集,而不能推广到看不见的数据。这里引入正则化项是为了惩罚较大的权重,因为权重现在成为最小化成本的一部分。因此,正则化消除了过拟合。最后,参数α提供了对数损失和泛化之间的权衡。如果 α 太小,则无法压缩大的权重,模型可能会出现高方差或过拟合;另一方面,如果 α 过大,模型可能会过度泛化,在拟合数据集方面表现不佳,这就是拟合不足的综合症。 α 是一个重要的参数进行调整,以获得最佳的正则化逻辑回归模型。
至于在 L1 和 L2 形态之间选择,经验法则是基于是否期望特征选择。在机器学习分类中,特征选择是挑选重要特征子集的过程,用于更好的模型构建。实际上,并非数据集中的每一个特征都携带有对鉴别样本有用的信息;有些功能要么是冗余的,要么是不相关的,因此可以很少损失地丢弃。在逻辑回归分类器中,特征选择只能通过 L1 正则化来实现。为了理解这一点,让我们考虑两个权重向量, w 1 = (1,0) 和w2=(0.5,0.5);假设它们产生相同数量的对数损失,每个权重向量的 L1 和 L2 正则化项如下:
两个向量的 L1 项等价,而 w 2 的 L2 项小于 w 1 的项。这表明,与 L1 正则化相比,L2 正则化对由大大小小的权重组成的权重的惩罚更大。换句话说,L2 正则化倾向于所有权重的相对小的值,并且避免任何权重的显著大的和小的值,而 L1 正则化允许一些权重具有显著小的值和一些权重具有显著大的值。只有通过 L1 正则化,才能将部分权重压缩到接近或精确到 0 ,从而实现特征选择。
在 scikit-learn 中,正则化类型可以通过penalty参数指定,选项有none(无正则化)、"l1"、"l2"和"elasticnet"(L1 和 L2 的混合),乘数α可以通过 alpha 参数指定。
使用 L1 正则化的特征选择
我们在这里检查 L1 正则化用于特征选择。
使用 L1 正则化初始化 SGD 逻辑回归模型,并基于 10,000 个样本训练模型:
>>> sgd_lr_l1 = SGDClassifier(loss='log', penalty='l1', alpha=0.0001, fit_intercept=True, max_iter=10,
learning_rate='constant', eta0=0.01)
>>> sgd_lr_l1.fit(X_train_enc.toarray(), Y_train)
利用训练好的模型,我们获得了其系数的绝对值:
>>> coef_abs = np.abs(sgd_lr_l1.coef_)
>>> print(coef_abs)
[[0\. 0.09963329 0\. ... 0\. 0\. 0.07431834]]
底部10系数及其值打印如下:
>>> print(np.sort(coef_abs)[0][:10])
[0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0.]
>>> bottom_10 = np.argsort(coef_abs)[0][:10]
我们可以通过以下代码了解这 10 个特性:
>>> feature_names = enc.get_feature_names()
>>> print('10 least important features are:\n',
feature_names[bottom_10])
10 least important features are:
['x0_1001' 'x8_851897aa' 'x8_85119990' 'x8_84ebbcd4' 'x8_84eb6b0e'
'x8_84dda655' 'x8_84c2f017' 'x8_84ace234' 'x8_84a9d4ba' 'x8_84915a27']
它们是X_train中0列的1001(即C1列)8列的"851897aa"等等。
类似地,前 10 个系数和它们的值可以得到如下:
>>> print(np.sort(coef_abs)[0][-10:])
[0.67912376 0.70885933 0.79975917 0.8828797 0.98146351 0.98275124
1.08313767 1.13261091 1.18445527 1.40983505]
>>> top_10 = np.argsort(coef_abs)[0][-10:]
>>> print('10 most important features are:\n', feature_names[top_10])
10 most important features are:
['x7_cef3e649' 'x3_7687a86e' 'x18_61' 'x18_15' 'x5_9c13b419'
'x5_5e3f096f' 'x2_763a42b5' 'x2_d9750ee7' 'x3_27e3c518'
'x5_1779deee']
分别是X_train中7列的"cef3e649"(即app_category)、【第三列的"7687a86e"(即site_domain)等等。
通过在线学习在大型数据集上进行培训
到目前为止,我们已经在不超过 30 万个样本上训练了我们的模型。如果我们超过这个数字,内存可能会过载,因为它容纳了太多的数据,程序会崩溃。在本节中,我们将探索如何使用在线学习在大规模数据集上进行训练。
SGD 是从梯度下降进化而来的,通过一次一个训练样本地顺序更新模型,而不是一次更新整个训练集。我们可以通过在线学习技术进一步扩大 SGD。在在线学习中,用于培训的新数据可以按顺序或实时获得,而不是在离线学习环境中一次性获得。一次加载和预处理相对较小的数据块用于训练,这释放了用于保存整个大数据集的内存。除了更好的计算可行性之外,在线学习也被使用,因为它适应实时生成新数据的情况,并且是模型现代化所需要的。例如,股票价格预测模型通过及时的市场数据以在线学习的方式更新;点击率预测模型需要包含反映用户最新行为和口味的最新数据;垃圾邮件检测器必须通过考虑动态生成的新功能来应对不断变化的垃圾邮件发送者。
由先前数据集训练的现有模型现在可以仅基于最近可用的数据集进行更新,而不是像离线学习中那样,基于先前和最近的数据集从头开始重建:
图 5.7:在线学习与离线学习
在前面的例子中,在线学习允许模型使用新到达的数据继续训练。然而,在离线学习中,我们必须用新到达的数据和旧数据重新训练整个模型。
scikit-learn 中的SGDClassifier模块通过partial_fit方法实现在线学习(而fit方法应用于离线学习,正如您所见)。我们将用 1,000,000 个样本来训练模型,其中我们一次输入 100,000 个样本来模拟在线学习环境。我们将在另外 100,000 个样本上测试训练好的模型,如下所示:
>>> n_rows = 100000 * 11
>>> df = pd.read_csv("train", nrows=n_rows)
>>> X = df.drop(['click', 'id', 'hour', 'device_id', 'device_ip'],
axis=1).values
>>> Y = df['click'].values
>>> n_train = 100000 * 10
>>> X_train = X[:n_train]
>>> Y_train = Y[:n_train]
>>> X_test = X[n_train:]
>>> Y_test = Y[n_train:]
将编码器安装在整个训练装置上,如下所示:
>>> enc = OneHotEncoder(handle_unknown='ignore')
>>> enc.fit(X_train)
初始化一个 SGD 逻辑回归模型,我们将迭代次数设置为1,以便部分拟合模型并启用在线学习:
>>> sgd_lr_online = SGDClassifier(loss='log', penalty=None,
fit_intercept=True, max_iter=1,
learning_rate='constant', eta0=0.01)
循环每个100000样本,并部分拟合模型:
>>> start_time = timeit.default_timer()
>>> for i in range(10):
... x_train = X_train[i*100000:(i+1)*100000]
... y_train = Y_train[i*100000:(i+1)*100000]
... x_train_enc = enc.transform(x_train)
... sgd_lr_online.partial_fit(x_train_enc.toarray(), y_train,
classes=[0, 1])
再次,我们使用partial_fit方法进行在线学习。另外,我们指定classes参数,这是在线学习所必需的:
>>> print(f"--- {(timeit.default_timer() - start_time)}.3fs seconds ---")
--- 167.399s seconds ---
将训练好的模型应用于测试集,即接下来的 100,000 个样本,如下所示:
>>> x_test_enc = enc.transform(X_test)
>>> pred = sgd_lr_online.predict_proba(x_test_enc.toarray())[:, 1]
>>> print(f'Training samples: {n_train * 10}, AUC on testing set: {roc_auc_score(Y_test, pred):.3f}')
Training samples: 10000000, AUC on testing set: 0.761
通过在线学习,基于总共 100 万个样本的训练只需要 167 秒,并且产生更好的准确性。
到目前为止,我们一直使用逻辑回归进行二元分类。我们能用它来处理多类案例吗?是的。然而,我们确实需要做一些小的调整。让我们在下一节看到这一点。
处理多类分类
最后一件值得注意的事情是逻辑回归算法如何处理多类分类。虽然我们在多类情况下与 scikit-learn 分类器的交互方式与在二进制情况下相同,但是理解逻辑回归在多类分类中的工作原理是很有用的。
超过两类的逻辑回归也被称为多项式逻辑回归,或者更广为人知的后来被称为软最大回归。正如您在二进制情况下看到的,模型由一个权重向量 w 表示,目标为 1 或正类的概率写如下:
在 K 类情况下,模型由 K 权向量、wT6】1、wT10】2 表示,..., w K ,目标为类 k 的概率写如下:
注意术语将概率
( k 从 1 到 K )归一化,使得它们总计为 1 。二进制情况下的成本函数表示如下:
同样,多类情况下的成本函数如下:
在这里,函数只有在
为真时才为 1 ,否则为 0 。
在定义了成本函数的情况下,我们获得了 j 权重向量的步长,就像我们在二进制情况下获得步长⇼w一样:
以类似的方式,在每次迭代中更新所有 K 权重向量。经过充分的迭代,学习到的权重向量,w1w2,...然后, w K 用于通过以下公式对新样品 x 进行分类:
为了更好地理解,让我们用一个经典的数据集进行实验,用于分类的手写数字:
>>> from sklearn import datasets
>>> digits = datasets.load_digits()
>>> n_samples = len(digits.images)
由于图像数据存储在 8*8 矩阵中,我们需要将其展平,如下所示:
>>> X = digits.images.reshape((n_samples, -1))
>>> Y = digits.target
然后,我们将数据拆分如下:
>>> from sklearn.model_selection import train_test_split
>>> X_train, X_test, Y_train, Y_test = train_test_split(X, Y,
test_size=0.2, random_state=42)
然后,我们将网格搜索和交叉验证结合起来,找到最优的多类逻辑回归模型,如下所示:
>>> from sklearn.model_selection import GridSearchCV
>>> parameters = {'penalty': ['l2', None],
... 'alpha': [1e-07, 1e-06, 1e-05, 1e-04],
... 'eta0': [0.01, 0.1, 1, 10]}
>>> sgd_lr = SGDClassifier(loss='log', learning_rate='constant',
eta0=0.01, fit_intercept=True, max_iter=10)
>>> grid_search = GridSearchCV(sgd_lr, parameters,
n_jobs=-1, cv=3)
>>> grid_search.fit(term_docs_train, label_train)
>>> print(grid_search.best_params_)
{'alpha': 1e-07, 'eta0': 0.1, 'penalty': None}
为了使用最优模型进行预测,我们应用以下内容:
>>> sgd_lr_best = grid_search.best_estimator_
>>> accuracy = sgd_lr_best.score(term_docs_test, label_test)
>>> print(f'The accuracy on testing set is: {accuracy*100:.1f}%')
The accuracy on testing set is: 94.2%
看起来和前面的例子没什么不同,因为SGDClassifier内部处理多类。请随意计算混淆矩阵作为练习。看看模型在单个类上的表现会很有趣。
下一部分将是奖励部分,我们将使用 TensorFlow 实现逻辑回归,并以点击预测为例。
使用 TensorFlow 实现逻辑回归
我们在此将前 30 万个样本的 90%用于训练,其余 10%用于测试,并假设X_train_enc、Y_train、X_test_enc和Y_test包含正确的数据:
-
首先我们导入 TensorFlow,将
X_train_enc、X_test_enc变换成numpy阵,施放X_train_enc、Y_train、X_test_enc、Y_test到【T7:>>> import tensorflow as tf >>> X_train_enc = X_train_enc.toarray().astype('float32') >>> X_test_enc = X_test_enc.toarray().astype('float32') >>> Y_train = Y_train.astype('float32') >>> Y_test = Y_test.astype('float32') -
We use the
tf.dataAPI to shuffle and batch data:>>> batch_size = 1000 >>> train_data = tf.data.Dataset.from_tensor_slices((X_train_enc, Y_train)) >>> train_data = train_data.repeat().shuffle(5000).batch(batch_size).prefetch(1)每次权重更新,只消耗一批样本,而不是一个样本或整个训练集。该模型基于一批样本计算的误差移动一步。在本例中,批次大小为 1,000。
-
然后,我们定义逻辑回归模型的权重和偏差:
>>> n_features = int(X_train_enc.shape[1]) >>> W = tf.Variable(tf.zeros([n_features, 1])) >>> b = tf.Variable(tf.zeros([1])) -
然后,我们创建一个梯度下降优化器,通过最小化损失来搜索最佳系数。我们在这里使用 Adam 作为优化器,它是一种高级梯度下降,具有自适应梯度的学习率(从 0.0008 开始):
>>> learning_rate = 0.0008 >>> optimizer = tf.optimizers.Adam(learning_rate) -
We define the optimization process where we compute the current prediction and cost and update the model coefficients following the computed gradients:
>>> def run_optimization(x, y): ... with tf.GradientTape() as g: ... logits = tf.add(tf.matmul(x, W), b)[:, 0] ... cost = tf.reduce_mean( tf.nn.sigmoid_cross_entropy_with_logits( labels=y, logits=logits)) ... gradients = g.gradient(cost, [W, b]) ... optimizer.apply_gradients(zip(gradients, [W, b]))这里,
tf.GradientTape允许我们跟踪 TensorFlow 计算,并计算给定变量的梯度。 -
We run the training for 6,000 steps (one step is with one batch of random samples):
>>> training_steps = 6000 >>> for step, (batch_x, batch_y) in enumerate(train_data.take(training_steps), 1): ... run_optimization(batch_x, batch_y) ... if step % 500 == 0: ... logits = tf.add(tf.matmul(batch_x, W), b)[:, 0] ... loss = tf.reduce_mean( tf.nn.sigmoid_cross_entropy_with_logits( labels=batch_y, logits=logits)) ... print("step: %i, loss: %f" % (step, loss)) step: 500, loss: 0.448672 step: 1000, loss: 0.389186 step: 1500, loss: 0.413012 step: 2000, loss: 0.445663 step: 2500, loss: 0.361000 step: 3000, loss: 0.417154 step: 3500, loss: 0.359435 step: 4000, loss: 0.393363 step: 4500, loss: 0.402097 step: 5000, loss: 0.376734 step: 5500, loss: 0.372981 step: 6000, loss: 0.406973每走 500 步,我们计算并打印出当前成本,以检查培训绩效。如你所见,训练损失总体上在减少。
-
After the model is trained, we use it to make predictions on the testing set and report the AUC metric:
>>> logits = tf.add(tf.matmul(X_test_enc, W), b)[:, 0] >>> pred = tf.nn.sigmoid(logits) >>> auc_metric = tf.keras.metrics.AUC() >>> auc_metric.update_state(Y_test, pred) >>> print(f'AUC on testing set: {auc_metric.result().numpy():.3f}') AUC on testing set: 0.771我们能够通过基于 TensorFlow 的逻辑回归模型实现
0.771的AUC。您还可以调整学习速率、训练步骤数和其他超参数,以获得更好的性能。这将是本章结尾的一个有趣的练习。
您已经在上一节使用 L1 正则化的特征选择中看到了特征选择如何与 L1 正则化的逻辑回归一起工作,其中不重要特征的权重被压缩到接近或精确到 0。除了 L1 正则逻辑回归,随机森林是另一种常用的特征选择技术。让我们在下一节看到更多。
使用随机森林的特征选择
简单回顾一下,随机森林正在一组独立的决策树上打包。当在每个节点上搜索最佳分割点时,每个树考虑特征的随机子集。而且,在决策树中,只有那些重要的特征(以及它们的分裂值)被用来构成树节点。将森林视为一个整体:一个特征在树节点中使用的频率越高,它就越重要。换句话说,我们可以根据特征在所有树的节点中出现的次数来排列特征的重要性,并选择最重要的。
scikit-learn 中的一个训练好的RandomForestClassifier模块带有一个属性feature_importances_,表示特征重要性,它是以树节点中出现的比例来计算的。同样,我们将在具有 100,000 个 ad 点击样本的数据集上使用随机森林检查特征选择:
>>> from sklearn.ensemble import RandomForestClassifier
>>> random_forest = RandomForestClassifier(n_estimators=100,
criterion='gini', min_samples_split=30, n_jobs=-1)
>>> random_forest.fit(X_train_enc.toarray(), Y_train)
在拟合随机森林模型之后,我们获得特征重要性分数,如下所示:
>>> feature_imp = random_forest.feature_importances_
>>> print(feature_imp)
[1.60540750e-05 1.71248082e-03 9.64485853e-04 ... 5.41025913e-04
7.78878273e-04 8.24041944e-03]
看看下面的 10 个功能得分和相应的 10 个最不重要的功能:
>>> feature_names = enc.get_feature_names()
>>> print(np.sort(feature_imp)[:10])
[0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0\. 0.]
>>> bottom_10 = np.argsort(feature_imp)[:10]
>>> print('10 least important features are:\n', feature_names[bottom_10])
10 least important features are:
['x8_ea4912eb' 'x8_c2d34e02' 'x6_2d332391' 'x2_ca9b09d0'
'x2_0273c5ad' 'x8_92bed2f3' 'x8_eb3f4b48' 'x3_535444a1' 'x8_8741c65a'
'x8_46cb77e5']
现在,来看看的前 10 个特征得分和对应的 10 个最重要的特征:
>>> print(np.sort(feature_imp)[-10:])
[0.00809279 0.00824042 0.00885188 0.00897925 0.01080301 0.01088246
0.01270395 0.01392431 0.01532718 0.01810339]
>>> top_10 = np.argsort(feature_imp)[-10:]
>>> print('10 most important features are:\n', feature_names[top_10])
10 most important features are:
['x17_-1' 'x18_157' 'x12_300' 'x13_250' 'x3_98572c79' 'x8_8a4875bd' 'x14_1993' 'x15_2' 'x2_d9750ee7' 'x18_33']
在本节中,我们介绍了随机森林如何用于特征选择。
摘要
在本章中,我们继续研究在线广告点击率预测项目。这一次,我们通过一键编码技术克服了分类特征的挑战。然后,我们求助于一种新的分类算法,逻辑回归,因为它对大数据集具有很高的可扩展性。对逻辑回归算法的深入讨论始于逻辑函数的引入,这导致了算法本身的机制。接下来是如何使用梯度下降训练逻辑回归模型。
在手工实现逻辑回归分类器并在我们的点进数据集上测试之后,您学习了如何使用 SGD 以更高级的方式训练逻辑回归模型,并且我们相应地调整了我们的算法。我们还练习了如何使用 scikit-learn 中基于 SGD 的逻辑回归分类器,并将其应用到我们的项目中。
然后,我们继续解决我们在使用逻辑回归时可能面临的问题,包括消除过拟合的 L1 和 L2 正则化、用于大规模数据集培训的在线学习技术以及处理多类场景。您还学习了如何使用 TensorFlow 实现逻辑回归。最后,本章以将随机森林模型应用于特征选择作为 L1 正则逻辑回归的替代方法而结束。
您可能很好奇,我们如何在 4000 万个样本的整个数据集上高效地训练模型。在下一章中,我们将利用 Spark 和PySpark模块等工具来扩展我们的解决方案。
练习
- 在基于 logistic 回归的点进预测项目中,是否也可以在
SGDClassifier模型中调整penalty、eta0、alpha等超参数?你能达到的最高测试 AUC 是多少? - 在在线学习解决方案中,您能否尝试使用更多的训练样本,例如 1000 万个样本?
- 在基于 TensorFlow 的解决方案中,您能否调整学习速率、训练步骤数和其他超参数以获得更好的性能?
六、将预测扩展到万亿字节的点击日志
在前一章中,我们使用逻辑回归分类器开发了一个广告点击率预测器。我们通过对多达 100 万个点击日志样本进行高效训练,证明了该算法的高度可扩展性。在这一章中,我们将通过利用强大的并行计算(或者更具体地说,分布式计算)工具 Apache Spark 来进一步提高广告点击预测器的可扩展性。
本章将揭开 Apache Spark 如何用于在海量数据上扩展学习的神秘面纱,而不是将模型学习限制在一台机器上。我们还将使用 Python APIPySpark,探索点击日志数据,基于整个点击日志数据集开发分类解决方案,并评估性能,所有这些都以分布式方式进行。除此之外,我将介绍两种处理分类特征的方法:一种与计算机科学中的散列相关,而另一种融合了多种特征。它们也将在 Spark 中实现。
在本章中,我们将涵盖以下主题:
- Apache Spark 的主要组件
- Spark 装置
- 部署 Spark 应用
- PySpark 中的基本数据结构
- PySpark 中的核心编程
- 广告点击率预测在 PySpark 中的实现
- PySpark 中的数据探索性分析
- Spark 中的缓存和持久性
- 特征哈希及其在 PySpark 中的实现
- PySpark 中的特征交互及其实现
学习 Apache Spark 的基本知识
Apache Spark 是一个分布式集群计算框架,设计用于快速和通用的计算。这是一项开源技术,最初由加州大学伯克利分校的 AMPLab 开发。它为交互式查询和流处理数据编程提供了一个易于使用的界面。它之所以成为受欢迎的大数据分析工具,是因为其隐含的数据并行性,即它跨计算集群中的处理器并行自动化数据操作。用户只需要关注他们想要如何操作数据,而不用担心数据如何在所有计算节点之间分布,或者一个节点负责哪部分数据。
记住,这本书主要是关于机器学习的。因此,我们将只简单介绍 Spark 的基础知识,包括它的组件、安装、部署、数据结构和核心编程。
分解 Spark
我们将从 Spark 的主要组件开始,如下图所示:
图 6.1:Spark 的主要组件
让我们更详细地讨论它们:
-
星火核心:这是整个平台的基础和执行引擎。它提供任务分配、调度和内存计算。顾名思义,Spark 核心是所有其他功能的基础。它也可以通过多种语言的 API 公开,包括 Python、Java、Scala 和 r。
-
Spark SQL :这是一个建立在 Spark Core 之上的组件,它引入了一个名为数据框架的高级数据抽象。稍后我们将在 Spark 中讨论数据结构。Spark SQL 支持 Python、Java 和 Scala 中类似 SQL 的数据操作,非常适合结构化和半结构化数据。在本章中,我们将使用 Spark SQL 中的模块。
-
Spark Streaming :通过利用 Spark Core 的快速调度和内存计算能力,执行实时(或接近实时)数据分析。
-
MLlib :简称机器学习库,这是建立在之上的 Spark Core 的分布式机器学习框架。得益于其分布式架构和内存计算能力,它允许对大规模数据进行高效学习。在内存计算中,如果随机存取存储器 ( 随机存取存储器)有足够的容量,数据将保存在其中,而不是保存在磁盘上。这降低了内存成本以及在迭代过程中前后重新加载数据的成本。训练机器学习模型基本上是一个迭代学习过程。因此,Spark 的内存计算能力使其非常适用于机器学习建模。根据主要的性能基准,使用 MLlib 学习的速度是基于磁盘的解决方案的近 10 倍。在本章中,我们将使用 Spark MLlib 中的模块。
-
GraphX: This is another functionality built on top of Spark Core that focuses on distributed graph-based processing. PageRank and Pregel abstraction are two typical use cases.
本节的主要目标是将 Spark 理解为一个为快速计算而设计的分布式集群计算框架,它促进了数据分析和迭代学习。如果你正在寻找更多关于 Spark 的详细信息,在线上有很多有用的文档和教程,比如spark.apache.org/docs/latest…。
安装 Spark
出于学习的目的,现在让我们在本地计算机上安装 Spark(尽管它在服务器集群中更频繁地使用)。完整的说明可以在spark.apache.org/downloads.h…找到。有好几个版本,我们就以预建了 Apache Hadoop 2.7 的 2.4.5 版本(2020 年 2 月 05 日)为例。
在撰写本文时,最新的稳定版本是 2.4.5。虽然有一个预览版,3.0.0,但我觉得最新的稳定版已经足够入手了。看完这一章,你不会注意到 3.0 和 2.4.5 有什么不同。请注意,模块 pyspark.ml.feature.OneHotEncoderEstimator已被弃用,并在预览版(v 3.0.0 及以上版本)中删除。它的功能已经被 pyspark.ml.feature.OneHotEncoder完善了。
如下图截图所示,在第一步中选择 2.4.5 后,我们在第二步中选择预建的 Apache Hadoop 2.7 选项。然后,我们点击步骤 3 中的链接下载spark-2 . 4 . 5-bin-Hadoop 2 . 7 . tgz文件:
图 6.2:下载 Spark 的步骤
解压缩下载的文件。生成的文件夹包含一个完整的 Spark 包;您不需要做任何额外的安装。
在运行任何 Spark 程序之前,我们需要确保安装了以下依赖项:
- Java 8+,它包含在系统环境变量中
- Scala 版
为了检查 Spark 是否安装正确,我们运行了以下测试:
-
首先,我们通过在终端中键入以下命令,使用 Spark 近似计算 π 的值(注意
bin是spark-2.4.5-bin-hadoop2.7中的一个文件夹,所以记得在这个文件夹中运行以下命令):./bin/run-example SparkPi 10 -
It should print out something similar to the following (the values may differ):
Pi is roughly 3.141851141851142该测试实际上类似于以下测试:
./bin/spark-submit examples/src/main/python/pi.py 10 -
Next, we test the interactive shell with the following command:
./bin/pyspark --master local[2]这应该会打开一个 Python 解释器,如下图所示:
图 6.3:外壳中运行的 Spark
到目前为止,应该已经正确安装了 Spark 程序。我们将在接下来的章节中讨论命令(pyspark和spark-submit)。
启动和部署 Spark 计划
一个 Spark 程序可以自己运行,也可以在集群管理器上运行。第一个选项类似于用多个线程在本地运行一个程序,一个线程被认为是一个 Spark 作业工作者。当然,根本没有并行性,但这是一种快速简单的启动 Spark 应用的方法,我们将在本章中通过演示的方式以这种模式部署它。例如,我们可以运行以下脚本来启动 Spark 应用:
./bin/spark-submit examples/src/main/python/pi.py
这正是我们在上一节中所做的。或者,我们可以指定线程数:
./bin/spark-submit --master local[4] examples/src/main/python/pi.py
在前面的代码中,我们通过使用以下命令,使用四个工作线程(或者机器上有多少个内核)在本地运行 Spark:
./bin/spark-submit --master local[*] examples/src/main/python/pi.py
同样,我们可以通过将spark-submit替换为pyspark来启动交互外壳:
./bin/pyspark --master local[2] examples/src/main/python/pi.py
至于集群模式,它(版本 2.4.5)目前支持以下方法:
- 独立:这是启动 Spark 应用最简单的模式。意思是师傅和工人在同一台机器上。有关如何在独立集群模式下启动 Spark 应用的详细信息,请访问以下链接:spark.apache.org/docs/latest…。
- Apache Mesos :作为一个集中式的容错集群管理器,Mesos 是为管理分布式计算环境而设计的。在 Spark 中,当驱动程序提交任务进行调度时,Mesos 会确定哪些机器处理哪些任务。详见spark.apache.org/docs/latest…。
- Apache Hadoop 纱:这种方法中的任务调度器变成了纱,与前一种方法中的 Mesos 相反。纱,是的缩写。另一个资源协商者是 Hadoop 中的资源管理器。有了纱,Spark 可以更容易地集成到 Hadoop 生态系统(如 MapReduce、Hive 和文件系统)中。更多信息请访问以下链接:spark.apache.org/docs/latest…。
- Kubernetes :这是一个开源系统,提供以容器为中心的基础设施。它有助于自动化工作部署和管理,近年来越来越受欢迎。Spark 的 Kubernetes 还是很新的,但是如果你感兴趣的话,可以在下面的链接中阅读更多内容:https://Spark . Apache . org/docs/latest/running-on-kubernetes . html。
启动和部署 Spark 应用很容易。用 PySpark 编码怎么样?让我们在下一节看到。
PySpark 中的编程
本节提供了在 Spark 中使用 Python 编程的快速介绍。我们将从 Spark 中的基本数据结构开始。
弹性分布式数据集 ( RDD )是 Spark 中的主数据结构。它是对象的分布式集合,具有以下三个主要特征:
- 弹性:当任何节点出现故障时,受影响的分区将被重新分配到健康的节点,这使得 Spark 具有容错性
- 分布式:数据驻留在集群中的一个或多个节点上,可以并行操作
- 数据集:包含分区数据及其值或元数据的集合
在 2.0 版本之前,RDD 是 Spark 的主要数据结构。之后,它被 DataFrame 取代,data frame 也是一个分布式数据集合,但被组织成命名列。数据帧利用了 Spark SQL 的优化执行引擎。因此,它们在概念上类似于关系数据库中的表或 Python pandas库中的DataFrame对象。
尽管当前版本的 Spark 仍然支持 RDD,但强烈建议使用数据框编程。因此,我们不会花太多时间和 RDD 一起编程。感兴趣的话可以参考https://spark . Apache . org/docs/latest/rdd-programming-guide . html。
Spark 程序的入口点是创建 Spark 会话,这可以通过使用以下几行来完成:
>>> from pyspark.sql import SparkSession
>>> spark = SparkSession \
... .builder \
... .appName("test") \
... .getOrCreate()
请注意,如果我们在 PySpark shell 中运行它,则不需要这样做。就在我们旋转一个 PySpark 外壳(带./bin/pyspark)之后,一个 Spark 会话被自动创建。我们可以在以下链接查看正在运行的 Spark 应用:localhost:4040/jobs/。有关结果页面,请参考以下屏幕截图:
图 6.4:Spark 应用用户界面
通过 Spark 会话spark,可以通过读取文件(通常是这种情况)或手动输入来创建数据框对象。在以下示例中,我们将从 CSV 文件创建一个数据框对象df:
>>> df = spark.read.csv("examples/src/main/resources/people.csv",
header=True, sep=';')
CSV 文件people.csv中的列用;隔开。
一旦完成,我们将在localhost:4040/jobs/中看到完成的工作:
图 6.5:Spark 应用中已完成的作业列表
我们可以使用以下命令显示df对象的内容:
>>> df.show()
+-----+---+---------+
| name|age| job|
+-----+---+---------+
|Jorge| 30|Developer|
| Bob| 32|Developer|
+-----+---+---------+
我们可以使用以下命令计算的行数:
>>> df.count()
2
使用以下命令可以显示df对象的模式:
>>> df.printSchema()
root
|-- name: string (nullable = true)
|-- age: string (nullable = true)
|-- job: string (nullable = true)
可以按如下方式选择一列或多列:
>>> df.select("name").show()
+-----+
| name|
+-----+
|Jorge|
| Bob|
+-----+
>>> df.select(["name", "job"]).show()
+-----+---------+
| name| job|
+-----+---------+
|Jorge|Developer|
| Bob|Developer|
+-----+---------+
我们可以通过条件过滤行,例如,通过一列的值,使用以下命令:
>>> df.filter(df['age'] > 31).show()
+----+---+---------+
|name|age| job|
+----+---+---------+
| Bob| 32|Developer|
+----+---+---------+
我们将在下一节继续在 PySpark 中编程,在这里我们将使用 Spark 来解决广告点击率问题。
使用 Spark 学习海量点击日志
通常情况下,为了利用 Spark,数据是使用 Hadoop 分布式文件系统 ( HDFS )进行存储的,这是一个分布式文件系统,旨在存储大量数据,计算发生在集群上的多个节点上。出于演示目的,我们将把数据保存在本地机器上,并在本地运行 Spark。这与在分布式计算集群上运行它没有什么不同。
正在加载点击日志
为了在海量点击日志上训练模型,我们首先需要在 Spark 中加载数据。为此,我们采取了以下步骤:
-
We spin up the PySpark shell by using the following command:
./bin/pyspark --master local[*] --driver-memory 20G这里,我们指定了一个大的驱动程序内存,因为我们处理的数据集超过 6 GB。
驱动程序负责收集和存储来自执行者的处理结果。因此,大的驱动程序内存有助于完成处理大量数据的任务。
-
接下来,我们使用名为
CTR:>>> spark = SparkSession\ ... .builder\ ... .appName("CTR")\ ... .getOrCreate()的应用启动 Spark 会话
-
Then, we load the click log data from the
trainfile into a DataFrame object. Note that the data load functionspark.read.csvallows custom schemas, which guarantees data is loaded as expected, as opposed to automatically inferring schemas. So, first, we define the schema:>>> from pyspark.sql.types import StructField, StringType, StructType, IntegerType >>> schema = StructType([ ... StructField("id", StringType(), True), ... StructField("click", IntegerType(), True), ... StructField("hour", IntegerType(), True), ... StructField("C1", StringType(), True), ... StructField("banner_pos", StringType(), True), ... StructField("site_id", StringType(), True), ... StructField("site_domain", StringType(), True), ... StructField("site_category", StringType(), True), ... StructField("app_id", StringType(), True), ... StructField("app_domain", StringType(), True), ... StructField("app_category", StringType(), True), ... StructField("device_id", StringType(), True), ... StructField("device_ip", StringType(), True), ... StructField("device_model", StringType(), True), ... StructField("device_type", StringType(), True), ... StructField("device_conn_type", StringType(), True), ... StructField("C14", StringType(), True), ... StructField("C15", StringType(), True), ... StructField("C16", StringType(), True), ... StructField("C17", StringType(), True), ... StructField("C18", StringType(), True), ... StructField("C19", StringType(), True), ... StructField("C20", StringType(), True), ... StructField("C21", StringType(), True), ... ])模式的每个字段包含列名(如
id、click或hour)、数据类型(如integer或string)以及是否允许缺失值(在本例中是允许的)。 -
With the defined schema, we create a DataFrame object,
df:>>> df = spark.read.csv("file://path_to_file/train", schema=schema, header=True)记得用
train数据文件所在的绝对路径替换path_to_file。file://前缀表示从本地文件中读取数据。另一个前缀dbfs://用于存储在 HDFS 的数据。 -
我们现在按照如下方式再次检查模式:
>>> df.printSchema() root |-- id: string (nullable = true) |-- click: integer (nullable = true) |-- hour: integer (nullable = true) |-- C1: string (nullable = true) |-- banner_pos: string (nullable = true) |-- site_id: string (nullable = true) |-- site_domain: string (nullable = true) |-- site_category: string (nullable = true) |-- app_id: string (nullable = true) |-- app_domain: string (nullable = true) |-- app_category: string (nullable = true) |-- device_id: string (nullable = true) |-- device_ip: string (nullable = true) |-- device_model: string (nullable = true) |-- device_type: string (nullable = true) |-- device_conn_type: string (nullable = true) |-- C14: string (nullable = true) |-- C15: string (nullable = true) |-- C16: string (nullable = true) |-- C17: string (nullable = true) |-- C18: string (nullable = true) |-- C19: string (nullable = true) |-- C20: string (nullable = true) |-- C21: string (nullable = true) -
数据大小检查如下:
>>> df.count() 40428967 -
此外,我们需要删除几个几乎不提供信息的列。我们使用以下代码来实现:
>>> df = df.drop('id').drop('hour').drop('device_id').drop('device_ip') -
我们将该列从
click重命名为label,因为这将在下游操作中更频繁地消耗:>>> df = df.withColumnRenamed("click", "label") -
让我们看看 DataFrame 对象中的当前列:
>>> df.columns ['label', 'C1', 'banner_pos', 'site_id', 'site_domain', 'site_category', 'app_id', 'app_domain', 'app_category', 'device_model', 'device_type', 'device_conn_type', 'C14', 'C15', 'C16', 'C17', 'C18', 'C19', 'C20', 'C21']
检查完输入数据后,我们需要对数据进行拆分和缓存。
拆分和缓存数据
在这里,我们将数据分为训练集和测试集,如下所示:
>>> df_train, df_test = df.randomSplit([0.7, 0.3], 42)
在这种情况下,70%的样本用于训练,剩余的样本用于测试,随机种子一如既往地用于繁殖。
在我们对训练集df_train执行任何繁重的提升(如模型学习)之前,最好先缓存对象。在 Spark 中,缓存和持久性是降低计算开销的优化技术。这将 RDD 或数据帧操作的中间结果保存在内存和/或磁盘上。如果没有缓存或持久性,每当需要一个中间数据帧时,它将根据最初的创建方式再次被重新计算。根据存储级别的不同,持久性的表现也不同:
MEMORY_ONLY:对象只存储在内存中。如果它不适合内存,剩余部分将在每次需要时重新计算。DISK_ONLY:对象只保存在磁盘上。持久化对象可以直接从存储中提取,而无需重新计算。MEMORY_AND_DISK:对象存储在内存中,也可能在磁盘上。如果整个对象不适合内存,剩余的分区将存储在磁盘上,而不是每次需要时都重新计算。这是 Spark 中缓存和持久性的默认模式。它利用了内存存储的快速检索和磁盘存储的高可访问性和容量。
在 PySpark 中,缓存很简单。所需要的只是一个缓存方法。
让我们缓存训练和测试数据帧:
>>> df_train.cache()
DataFrame[label: int, C1: string, banner_pos: string, site_id: string, site_domain: string, site_category: string, app_id: string, app_domain: string, app_category: string, device_model: string, device_type: string, device_conn_type: string, C14: string, C15: string, C16: string, C17: string, C18: string, C19: string, C20: string, C21: string]
>>> df_train.count()
28297027
>>> df_test.cache()
DataFrame[label: int, C1: string, banner_pos: string, site_id: string, site_domain: string, site_category: string, app_id: string, app_domain: string, app_category: string, device_model: string, device_type: string, device_conn_type: string, C14: string, C15: string, C16: string, C17: string, C18: string, C19: string, C20: string, C21: string]
>>> df_test.count()
12131940
现在,我们已经为下游分析准备好了培训和测试数据。
热门编码分类特征
与前一章类似,我们需要通过执行以下步骤将分类特征编码成多组二进制特征:
-
In our case, the categorical features include the following:
>>> categorical = df_train.columns >>> categorical.remove('label') >>> print(categorical) ['C1', 'banner_pos', 'site_id', 'site_domain', 'site_category', 'app_id', 'app_domain', 'app_category', 'device_model', 'device_type', 'device_conn_type', 'C14', 'C15', 'C16', 'C17', 'C18', 'C19', 'C20', 'C21']在 PySpark 中,一键编码不像 scikit-learn 中那样直接(特别是
OneHotEncoder模块)。 -
We need to index each categorical column using the
StringIndexermodule:>>> from pyspark.ml.feature import StringIndexer >>> indexers = [ ... StringIndexer(inputCol=c, outputCol= "{0}_indexed".format(c)).setHandleInvalid("keep") ... for c in categorical ... ]setHandleInvalid("keep")句柄确保如果出现任何新的分类值,应用不会崩溃。尽量省略;您将看到与未知值相关的错误消息。 -
然后,我们使用
OneHotEncoderEstimator模块对每个单独的索引分类列执行一次热编码:>>> from pyspark.ml.feature import OneHotEncoderEstimator >>> encoder = OneHotEncoderEstimator( ... inputCols=[indexer.getOutputCol() for indexer in indexers], ... outputCols=["{0}_encoded".format(indexer.getOutputCol()) for indexer in indexers] ... ) -
Next, we concatenate all sets of generated binary vectors into a single one using the
VectorAssemblermodule:>>> from pyspark.ml.feature import VectorAssembler >>> assembler = VectorAssembler( ... inputCols=encoder.getOutputCols(), ... outputCol="features" ... )这将创建名为
features.的最终编码向量列 -
We chain all these three stages together into a pipeline with the
Pipelinemodule in PySpark, which better organizes our one-hot encoding workflow:>>> stages = indexers + [encoder, assembler] >>> from pyspark.ml import Pipeline >>> pipeline = Pipeline(stages=stages)变量
stages是编码所需的操作列表。 -
最后,我们可以将
pipeline单热编码模型拟合到训练集:>>> one_hot_encoder = pipeline.fit(df_train) -
完成后,我们使用训练好的编码器来转换训练集和测试集。对于训练集,我们使用以下代码:
>>> df_train_encoded = one_hot_encoder.transform(df_train) >>> df_train_encoded.show() -
At this point, we skip displaying the results as there are dozens of columns with several additional ones added on top of
df_train. However, we can see the one we are looking for, thefeaturescolumn, which contains the one-hot encoded results. Hence, we only select this column, along with the target variable:>>> df_train_encoded = df_train_encoded.select( ["label", "features"]) >>> df_train_encoded.show() +-----+--------------------+ |label| features| +-----+--------------------+ | 0|(31458,[5,7,3527,...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,788,4...| | 0|(31458,[5,7,1271,...| | 0|(31458,[5,7,1271,...| | 0|(31458,[5,7,1271,...| | 0|(31458,[5,7,1271,...| | 0|(31458,[5,7,1532,...| | 0|(31458,[5,7,4366,...| | 0|(31458,[5,7,14,45...| +-----+--------------------+ only showing top 20 rows特征列包含大小为
31458的稀疏向量。 -
不要忘记缓存
df_train_encoded,因为我们将使用它来迭代训练我们的分类模型:>>> df_train_encoded.cache() DataFrame[label: int, features: vector] -
为了释放一些空间,我们打开
df_train,因为我们将不再需要它:
```py
>>> df_train.unpersist()
DataFrame[label: int, C1: string, banner_pos: string, site_id: string, site_domain: string, site_category: string, app_id: string, app_domain: string, app_category: string, device_model: string, device_type: string, device_conn_type: string, C14: string, C15: string, C16: string, C17: string, C18: string, C19: string, C20: string, C21: string]
```
11. 现在,我们对测试集重复前面的步骤:
```py
>>> df_test_encoded = one_hot_encoder.transform(df_test)
>>> df_test_encoded = df_test_encoded.select(["label", "features"])
>>> df_test_encoded.show()
+-----+--------------------+
|label| features|
+-----+--------------------+
| 0|(31458,[5,7,788,4...|
| 0|(31458,[5,7,788,4...|
| 0|(31458,[5,7,788,4...|
| 0|(31458,[5,7,788,4...|
| 0|(31458,[5,7,788,4...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,14,45...|
| 0|(31458,[5,7,2859,...|
| 0|(31458,[1,7,651,4...|
+-----+--------------------+
only showing top 20 rows
>>> df_test_encoded.cache()
DataFrame[label: int, features: vector]
>>> df_test.unpersist()
DataFrame[label: int, C1: string, banner_pos: string, site_id: string, site_domain: string, site_category: string, app_id: string, app_domain: string, app_category: string, device_model: string, device_type: string, device_conn_type: string, C14: string, C15: string, C16: string, C17: string, C18: string, C19: string, C20: string, C21: string]
```
12. 如果你在浏览器中查看 Spark UI localhost:4040/jobs/,你会看到几个已经完成的作业,比如如下:

图 6.6:编码后完成的作业列表
有了编码的训练和测试集,我们现在可以训练我们的分类模型了。
训练和测试逻辑回归模型
我们将使用逻辑回归作为我们的例子,但是 PySpark 中还支持许多其他的分类模型,例如决策树分类器、随机森林、神经网络(我们将在第 8 章、使用人工神经网络预测股票价格)、线性 SVM 和朴素贝叶斯。详情请参考以下链接:https://spark . Apache . org/docs/latest/ml-classification-revolution . html # classification。
我们可以通过以下步骤训练和测试逻辑回归模型:
-
We first import the logistic regression module and initialize a model:
>>> from pyspark.ml.classification import LogisticRegression >>> classifier = LogisticRegression(maxIter=20, regParam=0.001, elasticNetParam=0.001)这里,我们将最大迭代次数设置为
20,正则化参数设置为0.001。 -
Now, we fit the model on the encoded training set:
>>> lr_model = classifier.fit(df_train_encoded)请注意这可能需要一段时间。您可以同时在 Spark 界面检查正在运行或已完成的作业。有关一些已完成的作业,请参考以下屏幕截图:
图 6.7:培训后完成的工作列表
注意,每个 RDDLossFunction 代表优化逻辑回归分类器的迭代。
-
在所有迭代之后,我们将训练好的模型应用于测试集:
>>> predictions = lr_model.transform(df_test_encoded) -
We cache the prediction results, as we will compute the prediction's performance:
>>> predictions.cache() DataFrame[label: int, features: vector, rawPrediction: vector, probability: vector, prediction: double] Take a look at the prediction DataFrame: >>> predictions.show() +-----+--------------------+--------------------+--------------------+----------+ |label| features| rawPrediction| probability|prediction| +-----+--------------------+--------------------+--------------------+----------+ | 0|(31458,[5,7,788,4...|[2.80267740289335...|[0.94282033454271...| 0.0| | 0|(31458,[5,7,788,4...|[2.72243908463177...|[0.93833781006061...| 0.0| | 0|(31458,[5,7,788,4...|[2.72243908463177...|[0.93833781006061...| 0.0| | 0|(31458,[5,7,788,4...|[2.82083664358057...|[0.94379146612755...| 0.0| | 0|(31458,[5,7,788,4...|[2.82083664358057...|[0.94379146612755...| 0.0| | 0|(31458,[5,7,14,45...|[4.44920221201642...|[0.98844714081261...| 0.0| | 0|(31458,[5,7,14,45...|[4.44920221201642...|[0.98844714081261...| 0.0| | 0|(31458,[5,7,14,45...|[4.44920221201642...|[0.98844714081261...| 0.0| | 0|(31458,[5,7,14,45...|[4.54759977096521...|[0.98951842852058...| 0.0| | 0|(31458,[5,7,14,45...|[4.54759977096521...|[0.98951842852058...| 0.0| | 0|(31458,[5,7,14,45...|[4.38991492595212...|[0.98775013592573...| 0.0| | 0|(31458,[5,7,14,45...|[4.38991492595212...|[0.98775013592573...| 0.0| | 0|(31458,[5,7,14,45...|[4.38991492595212...|[0.98775013592573...| 0.0| | 0|(31458,[5,7,14,45...|[4.38991492595212...|[0.98775013592573...| 0.0| | 0|(31458,[5,7,14,45...|[5.58870435258071...|[0.99627406423617...| 0.0| | 0|(31458,[5,7,14,45...|[5.66066729150822...|[0.99653187592454...| 0.0| | 0|(31458,[5,7,14,45...|[5.66066729150822...|[0.99653187592454...| 0.0| | 0|(31458,[5,7,14,45...|[5.61336061100621...|[0.99636447866332...| 0.0| | 0|(31458,[5,7,2859,...|[5.47553763410082...|[0.99582948965297...| 0.0| | 0|(31458,[1,7,651,4...|[1.33424801682849...|[0.79154243844810...| 0.0| +-----+--------------------+--------------------+--------------------+----------+ only showing top 20 rows该包含预测特征、地面真实情况、两类概率和最终预测(决策阈值为 0.5)。
-
我们使用带有
areaUnderROC评估指标的BinaryClassificationEvaluator功能评估测试装置上接收器操作特性 ( ROC )的曲线下面积 ( AUC )
我们因此能够获得 74.89%的 AUC。我们能做得更好吗?让我们在下一节看到。
基于 Spark 的分类变量特征工程
在本章中,我已经演示了如何使用 Spark 构建一个从海量点击日志中学习的广告点击预测器。到目前为止,我们一直在使用单热编码来使用分类输入。在本节中,我们将讨论两种流行的特征工程技术:特征散列和特征交互。
特征哈希是一热编码的替代方案,而特征交互是一热编码的变体。特征工程是指基于领域知识或定义的规则生成新的特征,以提高利用现有特征空间实现的学习性能。
散列分类特征
在机器学习中,特征哈希(也称为哈希技巧)是一种高效的方式来编码分类特征。它基于计算机科学中的散列函数,将可变大小的数据映射到固定(通常更小)大小的数据。通过一个例子更容易理解特征散列。
假设我们有三个特性:性别、站点 _ 域、设备 _ 型号:
| 性别 | 站点 _ 域 | 设备模型 | | 男性的 | 美国有线新闻网 | 三星电子 | | 女性的 | 字母表 | 苹果手机 | | 男性的 | 美国全国广播公司 | 华为 | | 男性的 | 脸谱网 | 小米 | | 女性的 | 字母表 | 苹果手机 |表 6.1:三个分类特征的示例数据
通过一热编码,这些将成为大小为 9 的特征向量,其来自 2(来自性别 ) + 4(来自站点 _ 域 ) + 3(来自设备 _ 模型)。通过特征散列,我们希望获得大小为 4 的特征向量。我们将散列函数定义为每个字符的 Unicode 代码点之和,然后将结果除以 4,并将余数作为散列输出。以第一行为例;我们有以下内容:
单词(m) + 单词(a) + 单词(l) + 单词+++ 单词(s) + 单词(u) + 单词(n) + 单词(g) =
109+97+108+101+……+115+117+110+103 = 1500
1500 % 4 = 0,也就是说我们可以将这个样本编码到**【1 0 0 0】中。类似地,如果余数为 1,样本被散列成【0,1,0,0】;【0,0,1,0】为样本,2 为余数;【0,0,0,1】**为 3 为余数的样品;等等。
同样,对于其他行,我们有以下内容:
| 性别 | 站点 _ 域 | 设备模型 | 散列结果 | | 男性的 | 美国有线新闻网 | 三星电子 | [1 0 0 0] | | 女性的 | 字母表 | 苹果手机 | [0 0 0 1] | | 男性的 | 美国全国广播公司 | 华为 | [0 1 0 0] | | 男性的 | 脸谱网 | 小米 | [1 0 0 0] | | 女性的 | 字母表 | 苹果手机 | [0 0 0 1] |表 6.2:示例数据的散列结果
最后,我们使用四维散列向量来表示原始数据,而不是九维一维热编码向量。
关于功能散列,有几点需要注意:
- 相同的输入将始终转换为相同的输出;例如,第二行和第五行。
- 两个不同的输入可能会转换为相同的输出,例如第一行和第四行。这个现象叫做哈希碰撞。
- 因此,选择最终的固定尺寸很重要。如果尺寸太小,会导致严重的碰撞和信息丢失。如果太大,基本上是冗余的一热编码。有了正确的大小,它将使哈希节省空间,同时保留重要信息,这将进一步有利于下游任务。
- 哈希是单向的,这意味着我们不能将输出转换为输入,而单向编码是双向映射。
现在让我们在点击预测项目中采用特征散列法。回想一下,一次性编码向量的大小是 31,458。如果我们选择 10,000 作为固定的散列大小,我们将能够将空间减少到三分之一以下,并减少训练分类模型所消耗的内存。此外,我们将看到与一次编码相比,执行特征散列的速度有多快,因为不需要跟踪所有列中的所有唯一值。
它只是通过内部散列函数将字符串值的每一行映射到一个稀疏向量,如下所示:
-
我们从开始从 PySpark 导入特征散列模块,并初始化一个输出大小为
10000:>>> from pyspark.ml.feature import FeatureHasher >>> hasher = FeatureHasher(numFeatures=10000, inputCols=categorical, outputCol="features")的特征散列器
-
We use the defined hasher to convert the input DataFrame:
>>> hasher.transform(df_train).select("features").show() +--------------------+ | features| +--------------------+ |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[29,1228,1...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[1228,1289...| |(10000,[746,1060,...| |(10000,[675,1228,...| |(10000,[1289,1695...| +--------------------+ only showing top 20 rows如你所见,得到的列 f
eatures的大小是10000。同样,在特征散列中没有训练或拟合。哈希器是预定义的映射。 -
为了更好地组织整个工作流,我们将散列器和分类模型链接到一个管道中:
>>> classifier = LogisticRegression(maxIter=20, regParam=0.000, elasticNetParam=0.000) >>> stages = [hasher, classifier] >>> pipeline = Pipeline(stages=stages) -
我们在训练集上拟合流水线模型如下:
>>> model = pipeline.fit(df_train) -
我们将训练好的模型应用于测试集,并记录预测结果:
>>> predictions = model.transform(df_test) >>> predictions.cache() -
我们根据 ROC 的 AUC 来评估其性能:
>>> ev = BinaryClassificationEvaluator(rawPredictionCol = "rawPrediction", metricName = "areaUnderROC") >>> print(ev.evaluate(predictions)) 0.7448097180769776
我们能够实现 74.48%的 AUC,这接近于之前一次热编码的 74.89%。最终,我们节省了大量的计算资源,并获得了相当的预测精度。这是一个胜利。
使用特征哈希,我们失去了可解释性,但获得了计算优势。
组合多个变量–功能交互
在点击日志数据的所有特征中,有些本身就是非常微弱的信号。比如关于是否有人会点击广告,性别本身并没有告诉我们太多,设备型号本身也没有提供太多信息。
然而,通过组合多个特征,我们将能够创建更强的合成信号。特征交互(也称特征穿越)将为此引入。对于数值特征,它通常通过乘以它们的倍数来生成新特征。
我们还可以定义任何我们想要的集成规则。例如,我们可以从两个原始特征家庭收入和家庭规模生成一个附加特征收入/人:
| 家庭收入 | 家庭规模 | 收入/人 | | Three hundred thousand | Two | One hundred and fifty thousand | | One hundred thousand | one | One hundred thousand | | Four hundred thousand | four | One hundred thousand | | Three hundred thousand | five | Sixty thousand | | Two hundred thousand | Two | One hundred thousand |表 6.3:基于现有数字特征生成新数字特征的示例
对于分类特征,特征交互成为对两个或更多特征的和操作。在下面的示例中,我们正在从两个原始特征性别和站点域生成一个附加特征性别:站点域:
| 性别 | 站点 _ 域 | 性别:站点 _ 域 | | 男性的 | 美国有线新闻网 | 男:美国有线电视新闻网 | | 女性的 | 字母表 | 女:abc | | 男性的 | 美国全国广播公司 | 男:全国广播公司 | | 男性的 | 脸谱网 | 男:脸书 | | 女性的 | 字母表 | 女:abc |表 6.4:基于现有特征生成新分类特征的示例
然后,我们使用一次性编码来转换字符串值。在六个一热编码特征(两个来自性别和四个来自站点 _ 域)的基础上,性别和站点 _ 域之间的特征交互增加了八个进一步的特征(二乘四)。
现在让我们在点击预测项目中采用特征交互。我们将以C14和C15这两个特性作为和交互的例子:
-
First, we import the feature interaction module,
RFormula, from PySpark:>>> from pyspark.ml.feature import RFormulaRFormula模型采用了描述特征如何相互作用的公式。例如, y ~ a + b 表示它接收特征 a 和 b ,并基于它们预测y; y ~ a + b + a:b 表示其基于特征 a 、 b 以及迭代项、 a 和 b 预测y; y ~ a + b + c + a:b 表示基于特征 a 、 b 、 c 以及迭代项 a 和b 来预测 y 。 -
我们需要相应地定义一个交互公式:
>>> cat_inter = ['C14', 'C15'] >>> cat_no_inter = [c for c in categorical if c not in cat_inter] >>> concat = '+'.join(categorical) >>> interaction = ':'.join(cat_inter) >>> formula = "label ~ " + concat + '+' + interaction >>> print(formula) label ~ C1+banner_pos+site_id+site_domain+site_category+app_id+app_domain+app_category+device_model+device_type+device_conn_type+C14+C15+C16+C17+C18+C19+C20+C21+C14:C15 -
Now, we can initialize a feature interactor with this formula:
>>> interactor = RFormula( ... formula=formula, ... featuresCol="features", ... labelCol="label").setHandleInvalid("keep")同样,这里的
setHandleInvalid("keep")手柄确保如果出现任何新的分类值,它不会崩溃。 -
We use the defined feature interactor to fit and transform the input DataFrame:
>>> interactor.fit(df_train).transform(df_train).select("features"). show() +--------------------+ | features| +--------------------+ |(54930,[5,7,3527,...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,788,4...| |(54930,[5,7,1271,...| |(54930,[5,7,1271,...| |(54930,[5,7,1271,...| |(54930,[5,7,1271,...| |(54930,[5,7,1532,...| |(54930,[5,7,4366,...| |(54930,[5,7,14,45...| +--------------------+ only showing top 20 rows由于
C14和C15的交互项,特征空间增加了 2 万多个特征。 -
同样,我们将特征交互器和分类模型链接到一个管道中,以组织整个工作流:
>>> classifier = LogisticRegression(maxIter=20, regParam=0.000, elasticNetParam=0.000) >>> stages = [interactor, classifier] >>> pipeline = Pipeline(stages=stages) >>> model = pipeline.fit(df_train) >>> predictions = model.transform(df_test) >>> predictions.cache() >>> from pyspark.ml.evaluation import BinaryClassificationEvaluator >>> ev = BinaryClassificationEvaluator(rawPredictionCol = "rawPrediction", metricName = "areaUnderROC") >>> print(ev.evaluate(predictions)) 0.7490392990518315
74.90%的 AUC,加上特征C14和C15之间的额外交互,比没有任何交互时的 74.89%有所提高。因此,特征交互略微提升了模型的性能。
摘要
在本章中,我们继续研究在线广告点击率预测项目。这一次,在并行计算工具 Apache Spark 的帮助下,我们能够在拥有数百万条记录的整个数据集上训练分类器。我们讨论了 Spark 的基础知识,包括它的主要组件、Spark 程序的部署、PySpark 的编程要点以及 Spark 的 Python 接口。然后,我们使用 PySpark 编程来探索点击日志数据。
您学习了如何执行一次性编码、缓存中间结果、基于整个点击日志数据集开发分类解决方案以及评估性能。此外,为了提高预测性能,我引入了两种特征工程技术:特征哈希和特征交互。我们在 PySpark 中实现它们也很有趣。
回顾我们的学习历程,从第二章**开始,我们就一直在研究分类问题,用朴素贝叶斯构建电影推荐引擎。实际上,我们已经涵盖了机器学习中所有强大且流行的分类模型。我们将在下一章继续解决回归问题;回归是监督学习中分类的兄弟。您将学习回归模型,包括线性回归、回归决策树和支持向量回归。
练习
- 在 one-hot 编码解决方案中,您能否使用 PySpark 中支持的不同分类器来代替逻辑回归,例如决策树、随机森林或线性 SVM?
- 在功能哈希解决方案中,您可以尝试其他哈希大小,如 5,000 或 20,000 吗?你观察到了什么?
- 在功能交互解决方案中,是否可以尝试其他交互,如
C1、C20? - 为了降低扩展维度,可以先使用特征交互,然后使用特征哈希吗?你能获得更高的 AUC 吗?
七、使用回归算法预测股票价格
在前一章中,我们使用 Spark 在大型点击数据集上训练了一个分类器。在这一章中,我们将解决一个大家都感兴趣的问题——预测股票价格。通过明智的投资致富——谁不感兴趣?!大量金融、交易甚至科技公司都在积极研究股市走势和股价预测。已经开发了多种方法来使用机器学习技术预测股票价格。在这里,我们将集中学习几种流行的回归算法,包括线性回归、回归树和回归森林以及支持向量回归,并利用它们来解决这个十亿(或万亿)美元的问题。
我们将在本章中讨论以下主题:
- 介绍股票市场和股票价格
- 什么是回归?
- 股票数据采集和特征工程
- 线性回归力学
- 实现线性回归(从头开始,使用 scikit-learn 和 TensorFlow)
- 回归树的机制
- 实现回归树(从头开始并使用 scikit-learn)
- 从回归树到回归林
- 支持向量回归机及其 scikit-learn 实现
- 回归性能评估
- 用回归算法预测股票价格
股票市场和股票价格概述
公司的股票意味着公司的所有权。股票的单一份额代表对公司的部分资产和收益的要求,与股票总数成比例。例如,如果一名投资者拥有一家公司的 50 股股票,而该公司总共有 1000 股流通股,则该投资者(或股东)将拥有并有权获得该公司 5%的资产和收益。
公司股票可以通过证券交易所和组织在股东和其他方之间进行交易。主要证券交易所包括纽约证券交易所、纳斯达克、伦敦证券交易所集团、上海证券交易所和香港证券交易所。股票交易价格的波动主要是由供求规律决定的。在任何一个时刻,供给是公众投资者手中的股票数量,需求是投资者想要购买的股票数量,股票价格上下波动以达到和保持均衡。
一般来说,投资者希望低买高卖。这听起来很简单,但实施起来很有挑战性,因为很难判断一只股票的价格会上涨还是下跌。有两种主要的研究试图理解导致价格变化的因素和条件,甚至预测未来的股票价格,基本面分析和技术分析:
- 基本面分析:这个流重点关注影响公司价值和业务的底层因素,包括宏观角度的整体经济和行业状况,微观角度的公司财务状况、管理层和竞争对手。
- 技术分析:另一方面这个流通过对过去交易活动的统计研究来预测未来的价格走势,包括价格走势、成交量和市场数据。通过机器学习技术预测价格是当今技术分析中的一个重要课题。
许多定量交易公司一直在使用机器学习来增强自动化和算法交易。在本章中,我们将作为一名定量分析师/研究员,探索如何用几种典型的机器学习回归算法预测股价。
什么是回归?
回归是机器学习中主要的监督学习类型之一。在回归中,训练集包含观测值(也称为特征)及其相关的连续目标值。回归的过程有两个阶段:
- 第一阶段是探索观测和目标之间的关系。这是训练阶段。
- 第二阶段是使用第一阶段的模式为未来的观察生成目标。这是预测阶段。
下图描述了整个过程:
图 7.1:回归中的训练和预测阶段
回归和分类的主要区别在于回归中的输出值是连续的,而分类中的输出值是离散的。这导致这两种监督学习方法的应用领域不同。分类基本上是用来确定想要的成员或特征,正如你在前面几章中看到的,比如电子邮件是否是垃圾邮件、新闻组主题或广告点击。另一方面,回归主要涉及估计结果或预测反应。
用线性回归估计连续目标的一个例子如下,我们试图用一组二维数据点拟合一条线:
图 7.2:线性回归示例
典型的机器学习回归问题包括以下几个方面:
- 根据位置、面积、卧室数量和浴室预测房价
- 基于关于系统进程和内存的信息估计功耗
- 零售需求预测
- 预测股票价格
我在这一节已经谈到了回归,并将在下一节简要介绍它在股票市场和交易中的使用。
挖掘股价数据
理论上,我们可以应用回归技术来预测特定股票的价格。然而,很难确保我们挑选的股票适合学习目的——它的价格应该遵循一些可学习的模式,它不可能受到前所未有的情况或不规则事件的影响。因此,我们在这里将重点关注最受欢迎的股票指数之一,以更好地说明和概括我们的价格回归方法。
我们先来介绍一下什么是指数。一个股票指数是对整个股票市场的一部分价值的一个统计测量。一个指数包括几只不同的股票,足以代表整个市场的一部分。指数的价格通常被计算为所选股票价格的加权平均值。
道琼斯工业平均指数是世界上建立时间最长、最受关注的指数之一。它由美国最重要的 30 只股票组成,如微软、苹果、通用电气和华特·迪士尼公司,约占整个美国市场价值的四分之一。您可以在finance.yahoo.com/quote/%5EDJ…的雅虎财经上查看其每日价格和表现:
图 7.3:雅虎财经每日价格和业绩截图
在每个交易日,股票的价格都会发生变化,并被实时记录下来。说明价格在一个时间单位(通常是一天,但也可以是一周或一个月)内变动的五个数值是关键的交易指标。它们如下:
- 开仓:给定交易日的起始价
- 收盘:当日最终价格
- 高位:当日股票交易的最高价格
- 低点:当日股票交易的最低价格
- 成交量:当日收盘前交易的股票总数
除 DJIA 以外的其他主要指数包括:
- 标准普尔 500(标准普尔 500 指数的简称)指数由美国 500 只最常交易的股票组成,占整个美国市场价值的 80%(finance.yahoo.com/quote/%5EGS…)
- 纳斯达克综合指数由纳斯达克交易的所有股票组成(finance.yahoo.com/quote/%5EIX…
- 罗素 2000 指数是美国 3000 家最大上市公司中最后 2000 家的集合(finance.yahoo.com/quote/%5ERU… T2)
- 伦敦富时 100 指数由伦敦证券交易所上市的市值最高的 100 家公司组成(finance.yahoo.com/quote/%5EFT… T2)
我们将重点关注 DJIA,并利用其历史价格和表现来预测未来价格。在接下来的部分中,我们将探索如何开发价格预测模型,特别是回归模型,以及哪些可以用作指标或预测特征。
功能工程入门
说到机器学习算法,首先要问的问题通常是有哪些特征可用或者预测变量是什么。
用来预测 DJIA 未来价格的驱动因素,即收盘价格,包括历史和当前开盘价格以及历史表现(高、低、成交量)。注意,当前或当天的表现(高位、低位、成交量)不应该包括在内,因为我们根本无法预见当天收盘前股票交易的最高和最低价格或交易的股票总数。
仅用上述四个指标预测收盘价似乎不太乐观,可能会导致拟合不足。因此,我们需要想办法生成更多的特征,以提高预测能力。概括地说,在机器学习中,特征工程是基于现有特征创建特定领域特征的过程,以提高机器学习算法的性能。
特征工程通常需要足够的领域知识,并且可能非常困难和耗时。实际上,用于解决机器学习问题的功能通常不是直接可用的,需要专门设计和构建,例如垃圾邮件检测和新闻组分类中的术语频率或 tf-idf 功能。因此,特征工程在机器学习中是必不可少的,并且通常是我们花费最多精力来解决实际问题的地方。
在做投资决定时,投资者通常会看一段时间内的历史价格,而不仅仅是前一天的价格。因此,在我们的股价预测案例中,我们可以将过去一周(五个交易日)、过去一个月和过去一年的平均收盘价计算为三个新特征。我们还可以将时间窗口定制为我们想要的大小,例如过去一个季度或过去六个月。在这三个平均价格特征的基础上,我们可以通过计算三个不同时间范围内每对平均价格之间的比率来生成与价格趋势相关联的新特征,例如,过去一周和过去一年的平均价格之间的比率。
除了价格,成交量是投资者分析的另一个重要因素。同样,我们可以通过计算几个不同时间段的平均体积和每对平均值之间的比率来生成新的基于体积的特征。
除了一个时间窗口内的历史平均值,投资者还会大量考虑股票的波动性。波动率描述给定股票或指数的价格随时间变化的程度。用统计学术语来说,基本上就是收盘价的标准差。我们可以通过计算特定时间范围内收盘价的标准偏差以及交易量的标准偏差,轻松生成新的特征集。以类似的方式,每对标准偏差值之间的比率可以包含在我们的工程特征池中。
最后但同样重要的是,回报是投资者密切关注的一个重要财务指标。回报率是股票/指数在特定时期内收盘价的收益或损失百分比。例如,日回报和年回报是我们经常听到的财务术语。它们的计算方法如下:
这里,价格 i 是IT6 日的价格,价格T10【IT12】-1 是前一天的价格。周回报和月回报可以用类似的方式计算。根据每日收益,我们可以得出特定天数内的移动平均线。
例如,给定过去一周的每日回报、、
、
、
和
,我们可以计算该周的移动平均线如下:
总之,我们可以通过应用特征工程技术生成以下预测变量:
图 7.4:生成的特征(1)
图 7.5:生成的特征(2)
最终,我们能够生成总共 31 组特征,以及以下六个原始特征:
- 开盘价 i :此功能代表开盘价
- 开盘价 i-1 :此功能代表过去一天的开盘价
- 收盘价 i-1 :此功能代表过去一天的收盘价
- 高价 i-1 :此功能代表过去一天的最高价格
- 低价 i-1 :此功能代表过去一天的最低价
- 体积 i-1 :该特征表示过去一天的体积
获取数据和生成特征
为了便于参考,我们将在这里而不是在后面的章节中实现生成特征的代码。我们将从获取项目所需的数据集开始。
在整个项目中,我们将从雅虎金融获取股票指数价格和业绩数据。比如在历史数据页面finance.yahoo.com/quote/%5EDJ…我们可以把Time Period改成Dec 01, 2005 – Dec10, 2005,在Show中选择Historical Prices,在Frequency 中选择Daily (或者直接打开这个链接:finance.yahoo.com/quote/%5EDJ…,然后点击应用按钮。点击下载数据按钮下载数据并命名文件20051201_20051210.csv。
我们可以加载刚刚下载的数据,如下所示:
>>> mydata = pd.read_csv('20051201_20051210.csv', index_col='Date')
>>> mydata
Open High Low Close
Date
2005-12-01 10806.030273 10934.900391 10806.030273 10912.570312
2005-12-02 10912.009766 10921.370117 10861.660156 10877.509766
2005-12-05 10876.950195 10876.950195 10810.669922 10835.009766
2005-12-06 10835.410156 10936.200195 10835.410156 10856.860352
2005-12-07 10856.860352 10868.059570 10764.009766 10810.910156
2005-12-08 10808.429688 10847.250000 10729.669922 10755.120117
2005-12-09 10751.759766 10805.950195 10729.910156 10778.580078
Volume Adjusted Close
Date
2005-12-01 256980000.0 10912.570312
2005-12-02 214900000.0 10877.509766
2005-12-05 237340000.0 10835.009766
2005-12-06 264630000.0 10856.860352
2005-12-07 243490000.0 10810.910156
2005-12-08 253290000.0 10755.120117
2005-12-09 238930000.0 10778.580078
注意输出是一个pandas数据帧对象。Date栏为指标栏,其余栏为对应的财务变量。在下面几行代码中,您将看到 pandas 在简化关系(或类似表的)数据的数据分析和转换方面有多么强大。
首先,我们通过从一个子功能开始实现特征生成,该子功能从最初的六个特征直接创建特征,如下所示:
>>> def add_original_feature(df, df_new):
... df_new['open'] = df['Open']
... df_new['open_1'] = df['Open'].shift(1)
... df_new['close_1'] = df['Close'].shift(1)
... df_new['high_1'] = df['High'].shift(1)
... df_new['low_1'] = df['Low'].shift(1)
... df_new['volume_1'] = df['Volume'].shift(1)
然后,我们开发一个子函数,生成与平均收盘价相关的六个特征:
>>> def add_avg_price(df, df_new):
... df_new['avg_price_5'] =
df['Close'].rolling(5).mean().shift(1)
... df_new['avg_price_30'] =
df['Close'].rolling(21).mean().shift(1)
... df_new['avg_price_365'] =
df['Close'].rolling(252).mean().shift(1)
... df_new['ratio_avg_price_5_30'] =
df_new['avg_price_5'] / df_new['avg_price_30']
... df_new['ratio_avg_price_5_365'] =
df_new['avg_price_5'] / df_new['avg_price_365']
... df_new['ratio_avg_price_30_365'] =
df_new['avg_price_30'] / df_new['avg_price_365']
类似地,生成与平均体积相关的六个特征的子功能如下:
>>> def add_avg_volume(df, df_new):
... df_new['avg_volume_5'] =
df['Volume'].rolling(5).mean().shift(1)
... df_new['avg_volume_30'] =
df['Volume'].rolling(21).mean().shift(1)
... df_new['avg_volume_365'] =
df['Volume'].rolling(252).mean().shift(1)
... df_new['ratio_avg_volume_5_30'] =
df_new['avg_volume_5'] / df_new['avg_volume_30']
... df_new['ratio_avg_volume_5_365'] =
df_new['avg_volume_5'] / df_new['avg_volume_365']
... df_new['ratio_avg_volume_30_365'] =
df_new['avg_volume_30'] / df_new['avg_volume_365']
对于标准差,我们为价格相关特性开发了以下子函数:
>>> def add_std_price(df, df_new):
... df_new['std_price_5'] =
df['Close'].rolling(5).std().shift(1)
... df_new['std_price_30'] =
df['Close'].rolling(21).std().shift(1)
... df_new['std_price_365'] =
df['Close'].rolling(252).std().shift(1)
... df_new['ratio_std_price_5_30'] =
df_new['std_price_5'] / df_new['std_price_30']
... df_new['ratio_std_price_5_365'] =
df_new['std_price_5'] / df_new['std_price_365']
... df_new['ratio_std_price_30_365'] =
df_new['std_price_30'] / df_new['std_price_365']
类似地,生成六个基于体积的标准偏差特征的子函数如下:
>>> def add_std_volume(df, df_new):
... df_new['std_volume_5'] =
df['Volume'].rolling(5).std().shift(1)
... df_new['std_volume_30'] =
df['Volume'].rolling(21).std().shift(1)
... df_new['std_volume_365'] =
df['Volume'].rolling(252).std().shift(1)
... df_new['ratio_std_volume_5_30'] =
df_new['std_volume_5'] / df_new['std_volume_30']
... df_new['ratio_std_volume_5_365'] =
df_new['std_volume_5'] / df_new['std_volume_365']
... df_new['ratio_std_volume_30_365'] =
df_new['std_volume_30'] / df_new['std_volume_365']
使用以下子功能生成七个基于返回的特征:
>>> def add_return_feature(df, df_new):
... df_new['return_1'] = ((df['Close'] - df['Close'].shift(1))
/ df['Close'].shift(1)).shift(1)
... df_new['return_5'] = ((df['Close'] - df['Close'].shift(5))
/ df['Close'].shift(5)).shift(1)
... df_new['return_30'] = ((df['Close'] -
df['Close'].shift(21)) / df['Close'].shift(21)).shift(1)
... df_new['return_365'] = ((df['Close'] -
df['Close'].shift(252)) / df['Close'].shift(252)).shift(1)
... df_new['moving_avg_5'] =
df_new['return_1'].rolling(5).mean().shift(1)
... df_new['moving_avg_30'] =
df_new['return_1'].rolling(21).mean().shift(1)
... df_new['moving_avg_365'] =
df_new['return_1'].rolling(252).mean().shift(1)
最后,我们将调用前面所有子函数的主要特征生成函数放在一起:
>>> def generate_features(df):
... """
... Generate features for a stock/index based on historical price and performance
... @param df: dataframe with columns "Open", "Close", "High", "Low", "Volume", "Adjusted Close"
... @return: dataframe, data set with new features
... """
... df_new = pd.DataFrame()
... # 6 original features
... add_original_feature(df, df_new)
... # 31 generated features
... add_avg_price(df, df_new)
... add_avg_volume(df, df_new)
... add_std_price(df, df_new)
... add_std_volume(df, df_new)
... add_return_feature(df, df_new)
... # the target
... df_new['close'] = df['Close']
... df_new = df_new.dropna(axis=0)
... return df_new
注意这里的窗口大小是 5、21 和 252,而不是代表周、月和年窗口的 7、30 和 365 。这是因为一年有 252 个(四舍五入)交易日,一个月有 21 个交易日,一周有 5 个交易日。
我们可以对 1988 年至 2019 年查询的 DJIA 数据应用这一特征工程策略,如下(或直接从本页下载:finance.yahoo.com/quote/%5EDJ… ):
>>> data_raw = pd.read_csv('19880101_20191231.csv', index_col='Date')
>>> data = generate_features(data_raw)
看看具有新功能的数据是什么样子的:
>>> print(data.round(decimals=3).head(5))
前面的命令行生成以下输出:
图 7.6:打印数据框前五行的截图
由于所有的特征和驱动因素都准备好了,我们现在将关注基于这些预测特征估计连续目标变量的回归算法。
线性回归估计
我们首先想到的回归模型是线性回归。顾名思义,这是否意味着使用线性函数拟合数据点?让我们探索一下。
线性回归是如何工作的?
简单来说,线性回归试图用二维空间的直线或三维空间的平面拟合尽可能多的数据点。它探索观测值和目标之间的线性关系,这种关系用线性方程或加权和函数来表示。给定一个带有 n 特征的数据样本 x ,xT8】1,xT12】2,…,xT16】n(x代表一个特征向量并且x =(xT22】1T24】,xT26】2 以及线性回归模型 w ( w 表示向量(wT42】1,wT46】2,…,wT50】n)的权重(也称为系数),目标 y 表示如下:
同样,有时线性回归模型带有一个截距(也称为偏差)wT7】0,因此前面的线性关系如下:
看起来眼熟吗?您在第五章、中学习的逻辑回归算法,用逻辑回归预测在线广告点击率,只是在线性回归的基础上增加了逻辑变换,将连续加权和映射到 0 (负)或 1 (正)类。类似地,从训练数据中学习线性回归模型,或者具体地说是其权重向量 w ,目标是将定义的估计误差最小化为均方误差 ( 均方误差,其测量真实值和预测值之间的差值的平方的平均值。给定 m 训练样本,( x (1) 、 y (1) )、(xT29】(2)、 y (2) )、……(xT37】(T39】I y(m)),关于待优化权重的成本函数 J(w) 表示如下:
这里,是预测。
同样,我们可以获得最优的 w ,从而使用梯度下降使 J(w) 最小化。一阶导数,梯度∮w,推导如下:
结合梯度和学习率η,权重向量 w 可以在每一步更新如下:
在大量的迭代之后,学习的 w 然后被用于预测新的样本,如下所示:
了解了线性回归背后的数学理论后,让我们在下一节从头开始实现它。
从头开始实现线性回归
既然你对基于梯度下降的线性回归有了透彻的了解,我们就从头开始实现。
我们首先用当前权重定义计算预测的函数:
>>> def compute_prediction(X, weights):
... """
... Compute the prediction y_hat based on current weights
... """
... predictions = np.dot(X, weights)
... return predictions
然后,我们继续更新权重 w 的函数,以梯度下降的方式进行一步,如下所示:
>>> def update_weights_gd(X_train, y_train, weights,
learning_rate):
... """
... Update weights by one step and return updated wights
... """
... predictions = compute_prediction(X_train, weights)
... weights_delta = np.dot(X_train.T, y_train - predictions)
... m = y_train.shape[0]
... weights += learning_rate / float(m) * weights_delta
... return weights
接下来,我们还添加了计算成本 J(w) 的函数:
>>> def compute_cost(X, y, weights):
... """
... Compute the cost J(w)
... """
... predictions = compute_prediction(X, weights)
... cost = np.mean((predictions - y) ** 2 / 2.0)
... return cost
现在,通过执行以下任务,将所有功能与模型训练功能放在一起:
- 在每次迭代中更新权重向量
- 打印出每 100 次(或任意次数)迭代的当前成本,以确保成本正在降低,并且一切都在正确的轨道上
让我们看看它是如何通过执行以下命令来完成的:
>>> def train_linear_regression(X_train, y_train, max_iter, learning_rate, fit_intercept=False):
... """
... Train a linear regression model with gradient descent, and return trained model
... """
... if fit_intercept:
... intercept = np.ones((X_train.shape[0], 1))
... X_train = np.hstack((intercept, X_train))
... weights = np.zeros(X_train.shape[1])
... for iteration in range(max_iter):
... weights = update_weights_gd(X_train, y_train,
weights, learning_rate)
... # Check the cost for every 100 (for example) iterations
... if iteration % 100 == 0:
... print(compute_cost(X_train, y_train, weights))
... return weights
最后,使用训练好的模型预测新输入值的结果,如下所示:
>>> def predict(X, weights):
... if X.shape[1] == weights.shape[0] - 1:
... intercept = np.ones((X.shape[0], 1))
... X = np.hstack((intercept, X))
... return compute_prediction(X, weights)
正如您刚刚看到的,实现线性回归与逻辑回归非常相似。让我们用一个小例子来检验它:
>>> X_train = np.array([[6], [2], [3], [4], [1],
[5], [2], [6], [4], [7]])
>>> y_train = np.array([5.5, 1.6, 2.2, 3.7, 0.8,
5.2, 1.5, 5.3, 4.4, 6.8])
基于包含截距的权重,以0.01的学习速率,通过100迭代训练线性回归模型:
>>> weights = train_linear_regression(X_train, y_train,
max_iter=100, learning_rate=0.01, fit_intercept=True)
按照以下步骤检查模型在新样品上的性能:
>>> X_test = np.array([[1.3], [3.5], [5.2], [2.8]])
>>> predictions = predict(X_test, weights)
>>> import matplotlib.pyplot as plt
>>> plt.scatter(X_train[:, 0], y_train, marker='o', c='b')
>>> plt.scatter(X_test[:, 0], predictions, marker='*', c='k')
>>> plt.xlabel('x')
>>> plt.ylabel('y')
>>> plt.show()
有关最终结果,请参考以下屏幕截图:
图 7.7:玩具数据集上的线性回归
我们训练的模型正确预测了新的样本(由星星描绘)。
让我们在另一个数据集上尝试一下,来自 scikit-learn 的糖尿病数据集:
>>> from sklearn import datasets
>>> diabetes = datasets.load_diabetes()
>>> print(diabetes.data.shape)
(442, 10)
>>> num_test = 30
>>> X_train = diabetes.data[:-num_test, :]
>>> y_train = diabetes.target[:-num_test]
基于包含截距的权重,以1的学习速率,通过5000迭代训练线性回归模型(每次500迭代显示成本):
>>> weights = train_linear_regression(X_train, y_train,
max_iter=5000, learning_rate=1, fit_intercept=True)
2960.1229915
1539.55080927
1487.02495658
1480.27644342
1479.01567047
1478.57496091
1478.29639883
1478.06282572
1477.84756968
1477.64304737
>>> X_test = diabetes.data[-num_test:, :]
>>> y_test = diabetes.target[-num_test:]
>>> predictions = predict(X_test, weights)
>>> print(predictions)
[ 232.22305668 123.87481969 166.12805033 170.23901231
228.12868839 154.95746522 101.09058779 87.33631249
143.68332296 190.29353122 198.00676871 149.63039042
169.56066651 109.01983998 161.98477191 133.00870377
260.1831988 101.52551082 115.76677836 120.7338523
219.62602446 62.21227353 136.29989073 122.27908721
55.14492975 191.50339388 105.685612 126.25915035
208.99755875 47.66517424]
>>> print(y_test)
[ 261\. 113\. 131\. 174\. 257\. 55\. 84\. 42\. 146\. 212\. 233\.
91\. 111\. 152\. 120\. 67\. 310\. 94\. 183\. 66\. 173\. 72\.
49\. 64\. 48\. 178\. 104\. 132\. 220\. 57.]
估计相当接近地面真相。
接下来,让我们利用 scikit-learn 实现线性回归。
用 scikit-learn 实现线性回归
到目前为止,我们已经在权重优化中使用了梯度下降,但是像逻辑回归一样,线性回归也对随机梯度下降 ( SGD 开放。要使用它,我们可以简单地将update_weights_gd功能替换为我们在第 5 章、中创建的update_weights_sgd功能,使用逻辑回归预测在线广告点击率。
我们也可以直接使用基于 SGD 的回归算法SGDRegressor,来自 scikit-learn:
>>> from sklearn.linear_model import SGDRegressor
>>> regressor = SGDRegressor(loss='squared_loss', penalty='l2',
alpha=0.0001, learning_rate='constant', eta0=0.01, max_iter=1000)
这里,loss参数的'squared_loss'表示成本函数为 MSEpenalty是正则化术语,可以是None、l1或l2,类似于第五章、用 Logistic 回归预测在线广告点击率中的SGDClassifier,以减少过度拟合;max_iter为迭代次数;其余两个参数表示学习率为0.01,在训练过程中保持不变。在测试集上训练模型并输出预测,如下所示:
>>> regressor.fit(X_train, y_train)
>>> predictions = regressor.predict(X_test)
>>> print(predictions)
[ 231.03333725 124.94418254 168.20510142 170.7056729
226.52019503 154.85011364 103.82492496 89.376184
145.69862538 190.89270871 197.0996725 151.46200981
170.12673917 108.50103463 164.35815989 134.10002755
259.29203744 103.09764563 117.6254098 122.24330421
219.0996765 65.40121381 137.46448687 123.25363156
57.34965405 191.0600674 109.21594994 128.29546226
207.09606669 51.10475455]
也可以用 TensorFlow 实现线性回归。让我们在下一节看到这一点。
用 TensorFlow 实现线性回归
首先,我们导入 TensorFlow 并构建模型:
>>> import tensorflow as tf
>>> layer0 = tf.keras.layers.Dense(units=1,
input_shape=[X_train.shape[1]])
>>> model = tf.keras.Sequential(layer0)
它用一个线性层(或者你可以把它想象成一个线性函数)把X_train.shape[1]维的输入和1维的输出连接起来。
接下来,我们指定损失函数、均方误差和学习率为1的梯度下降优化器Adam:
>>> model.compile(loss='mean_squared_error',
optimizer=tf.keras.optimizers.Adam(1))
现在我们训练模型 100 次迭代:
>>> model.fit(X_train, y_train, epochs=100, verbose=True)
Epoch 1/100
412/412 [==============================] - 1s 2ms/sample - loss: 27612.9129
Epoch 2/100
412/412 [==============================] - 0s 44us/sample - loss: 23802.3043
Epoch 3/100
412/412 [==============================] - 0s 47us/sample - loss: 20383.9426
Epoch 4/100
412/412 [==============================] - 0s 51us/sample - loss: 17426.2599
Epoch 5/100
412/412 [==============================] - 0s 44us/sample - loss: 14857.0057
……
Epoch 96/100
412/412 [==============================] - 0s 55us/sample - loss: 2971.6798
Epoch 97/100
412/412 [==============================] - 0s 44us/sample - loss: 2970.8919
Epoch 98/100
412/412 [==============================] - 0s 52us/sample - loss: 2970.7903
Epoch 99/100
412/412 [==============================] - 0s 47us/sample - loss: 2969.7266
Epoch 100/100
412/412 [==============================] - 0s 46us/sample - loss: 2970.4180
这也打印出每次迭代的损失。最后,我们使用训练好的模型进行预测:
>>> predictions = model.predict(X_test)[:, 0]
>>> print(predictions)
[231.52155 124.17711 166.71492 171.3975 227.70126 152.02522
103.01532 91.79277 151.07457 190.01042 190.60373 152.52274
168.92166 106.18033 167.02473 133.37477 259.24756 101.51256
119.43106 120.893005 219.37921 64.873634 138.43217 123.665634
56.33039 189.27441 108.67446 129.12535 205.06857 47.99469 ]
您将学习的下一个回归算法是决策树回归。
决策树回归估计
决策树回归也叫回归树。通过比较回归树和你已经熟悉的它的兄弟分类树,很容易理解回归树。
从分类树过渡到回归树
在分类中,决策树是通过递归的二进制分裂和将每个节点成长为左右子节点来构建的。在每个分区中,它贪婪地搜索最重要的特征组合及其值作为最佳分割点。分离的质量是通过两个孩子标签的加权纯度来衡量的,特别是通过基尼杂质或信息增益。在回归中,树的构建过程几乎与分类过程相同,只有两个区别,因为目标变得连续:
- 分裂点的质量现在由两个子节点的加权均方误差来衡量;子代的均方误差相当于所有目标值的方差,加权均方误差越小,分割越好
- 终端节点中目标的平均值值成为叶值,而不是分类树中的大多数标签
为了确保您理解回归树,让我们使用特征房屋类型和卧室数量来研究一个估算房价的小例子:
图 7.8:玩具房价数据集
我们首先定义将在我们的计算中使用的均方误差和加权均方误差计算函数:
>>> def mse(targets):
... # When the set is empty
... if targets.size == 0:
... return 0
... return np.var(targets)
然后,我们定义节点拆分后的加权均方误差:
>>> def weighted_mse(groups):
... """
... Calculate weighted MSE of children after a split
... """
... total = sum(len(group) for group in groups)
... weighted_sum = 0.0
... for group in groups:
... weighted_sum += len(group) / float(total) * mse(group)
... return weighted_sum
通过执行以下命令进行测试:
>>> print(f'{mse(np.array([1, 2, 3])):.4f}')
0.6667
>>> print(f'{weighted_mse([np.array([1, 2, 3]), np.array([1, 2])]):.4f}')
0.5000
为了构建房价回归树,我们首先穷尽所有可能的特征和值对,并计算相应的均方误差:
MSE(type, semi) = weighted_mse([[600, 400, 700], [700, 800]]) = 10333
MSE(bedroom, 2) = weighted_mse([[700, 400], [600, 800, 700]]) = 13000
MSE(bedroom, 3) = weighted_mse([[600, 800], [700, 400, 700]]) = 16000
MSE(bedroom, 4) = weighted_mse([[700], [600, 700, 800, 400]]) = 17500
利用type, semi对获得最低的均方误差,然后由这个分裂点形成根节点。这种划分的结果如下:
图 7.9:使用(类型=半)分割
如果我们对一个一级回归树感到满意,我们可以在此停止,将两个分支都指定为叶节点,其值作为包含的样本的目标的平均值。或者,我们可以通过从右分支构建第二个级别(左分支不能进一步拆分)来进一步发展:
MSE(bedroom, 2) = weighted_mse([[], [600, 400, 700]]) = 15556
MSE(bedroom, 3) = weighted_mse([[400], [600, 700]]) = 1667
MSE(bedroom, 4) = weighted_mse([[400, 600], [700]]) = 6667
随着bedroom, 3对指定的第二个分裂点(不管它是否至少有三个卧室)与最小均方误差,我们的树变成如下图所示:
图 7.10:分割使用(卧室> =3)
我们可以通过给两个叶节点分配平均值来结束树。
实现决策树回归
现在你已经清楚了回归树的构建过程,是时候编码了。
我们将在本节中定义的节点拆分实用程序功能与我们在第 4 章、中使用的基于树的算法预测在线广告点击率相同,它基于特征和值对将节点中的样本分成左右分支:
>>> def split_node(X, y, index, value):
... """
... Split data set X, y based on a feature and a value
... @param index: index of the feature used for splitting
... @param value: value of the feature used for splitting
... @return: left and right child, a child is in the format of [X, y]
... """
... x_index = X[:, index]
... # if this feature is numerical
... if type(X[0, index]) in [int, float]:
... mask = x_index >= value
... # if this feature is categorical
... else:
... mask = x_index == value
... # split into left and right child
... left = [X[~mask, :], y[~mask]]
... right = [X[mask, :], y[mask]]
... return left, right
接下来,我们定义贪婪搜索函数,尝试所有可能的拆分,并返回最小加权均方误差:
>>> def get_best_split(X, y):
... """
... Obtain the best splitting point and resulting children for the data set X, y
... @return: {index: index of the feature, value: feature value, children: left and right children}
... """
... best_index, best_value, best_score, children =
None, None, 1e10, None
... for index in range(len(X[0])):
... for value in np.sort(np.unique(X[:, index])):
... groups = split_node(X, y, index, value)
... impurity = weighted_mse(
[groups[0][1], groups[1][1]])
... if impurity < best_score:
... best_index, best_value, best_score, children
= index, value, impurity, groups
... return {'index': best_index, 'value': best_value,
'children': children}
前面的选择和拆分过程以递归方式在每个后续子对象上发生。当满足停止标准时,节点处的过程停止,样本的平均值targets将被分配给该终端节点:
>>> def get_leaf(targets):
... # Obtain the leaf as the mean of the targets
... return np.mean(targets)
最后,这里是递归函数,split,它把所有的一切联系在一起。它检查是否满足任何停止标准,如果满足,则分配叶节点,否则继续进一步分离:
>>> def split(node, max_depth, min_size, depth):
... """
... Split children of a node to construct new nodes or assign them terminals
... @param node: dict, with children info
... @param max_depth: maximal depth of the tree
... @param min_size: minimal samples required to further split a child
... @param depth: current depth of the node
... """
... left, right = node['children']
... del (node['children'])
... if left[1].size == 0:
... node['right'] = get_leaf(right[1])
... return
... if right[1].size == 0:
... node['left'] = get_leaf(left[1])
... return
... # Check if the current depth exceeds the maximal depth
... if depth >= max_depth:
... node['left'], node['right'] = get_leaf(
left[1]), get_leaf(right[1])
... return
... # Check if the left child has enough samples
... if left[1].size <= min_size:
... node['left'] = get_leaf(left[1])
... else:
... # It has enough samples, we further split it
... result = get_best_split(left[0], left[1])
... result_left, result_right = result['children']
... if result_left[1].size == 0:
... node['left'] = get_leaf(result_right[1])
... elif result_right[1].size == 0:
... node['left'] = get_leaf(result_left[1])
... else:
... node['left'] = result
... split(node['left'], max_depth, min_size, depth + 1)
... # Check if the right child has enough samples
... if right[1].size <= min_size:
... node['right'] = get_leaf(right[1])
... else:
... # It has enough samples, we further split it
... result = get_best_split(right[0], right[1])
... result_left, result_right = result['children']
... if result_left[1].size == 0:
... node['right'] = get_leaf(result_right[1])
... elif result_right[1].size == 0:
... node['right'] = get_leaf(result_left[1])
... else:
... node['right'] = result
... split(node['right'], max_depth, min_size,
depth + 1)
回归树构建的入口点如下:
>>> def train_tree(X_train, y_train, max_depth, min_size):
... root = get_best_split(X_train, y_train)
... split(root, max_depth, min_size, 1)
... return root
现在,让我们用一个手工计算的例子来测试它:
>>> X_train = np.array([['semi', 3],
... ['detached', 2],
... ['detached', 3],
... ['semi', 2],
... ['semi', 4]], dtype=object)
>>> y_train = np.array([600, 700, 800, 400, 700])
>>> tree = train_tree(X_train, y_train, 2, 2)
为了验证训练的树与我们手动构建的树相同,我们编写了一个显示树的函数:
>>> CONDITION = {'numerical': {'yes': '>=', 'no': '<'},
... 'categorical': {'yes': 'is', 'no': 'is not'}}
>>> def visualize_tree(node, depth=0):
... if isinstance(node, dict):
... if type(node['value']) in [int, float]:
... condition = CONDITION['numerical']
... else:
... condition = CONDITION['categorical']
... print('{}|- X{} {} {}'.format(depth * ' ',
node['index'] + 1, condition['no'],
node['value']))
... if 'left' in node:
... visualize_tree(node['left'], depth + 1)
... print('{}|- X{} {} {}'.format(depth * ' ',
node['index'] + 1, condition['yes'],
node['value']))
... if 'right' in node:
... visualize_tree(node['right'], depth + 1)
... else:
... print('{}[{}]'.format(depth * ' ', node))
>>> visualize_tree(tree)
|- X1 is not detached
|- X2 < 3
[400.0]
|- X2 >= 3
[650.0]
|- X1 is detached
[750.0]
既然你从零开始实现回归树后对回归树有了更好的理解,我们可以直接使用 scikit-learn 中的DecisionTreeRegressor包(https://sci kit-learn . org/stable/modules/generated/sklearn . tree . decision tree returnor . html)。让我们将它应用于预测波士顿房价的示例,如下所示:
>>> boston = datasets.load_boston()
>>> num_test = 10 # the last 10 samples as testing set
>>> X_train = boston.data[:-num_test, :]
>>> y_train = boston.target[:-num_test]
>>> X_test = boston.data[-num_test:, :]
>>> y_test = boston.target[-num_test:]
>>> from sklearn.tree import DecisionTreeRegressor
>>> regressor = DecisionTreeRegressor(max_depth=10,
min_samples_split=3)
>>> regressor.fit(X_train, y_train)
>>> predictions = regressor.predict(X_test)
>>> print(predictions)
[12.7 20.9 20.9 20.2 20.9 30.8
20.73076923 24.3 28.2 20.73076923]
将预测与基本事实进行如下比较:
>>> print(y_test)
[ 19.7 18.3 21.2 17.5 16.8 22.4 20.6 23.9 22\. 11.9]
在这一节中,我们实现了一个回归树。回归树有集成版吗?让我们看看下一个。
实现回归林
在第 4 章 *【基于树的算法预测在线广告点击率】*中,我们探索了随机森林作为一种集成学习方法,通过组合多个分别训练的决策树,并在树的每个节点随机子采样训练特征。在分类中,随机森林通过所有树决策的多数票做出最终决定。应用于回归,随机森林回归模型(也称为回归森林)将所有决策树的回归结果的平均值分配给最终决策。
在这里,我们将使用 scikit 的回归森林包RandomForestRegressor-学习并将其部署在我们的波士顿房价预测示例中:
>>> from sklearn.ensemble import RandomForestRegressor
>>> regressor = RandomForestRegressor(n_estimators=100,
max_depth=10, min_samples_split=3)
>>> regressor.fit(X_train, y_train)
>>> predictions = regressor.predict(X_test)
>>> print(predictions)
[ 19.34404351 20.93928947 21.66535354 19.99581433 20.873871
25.52030056 21.33196685 28.34961905 27.54088571 21.32508585]
我们要探索的第三个回归算法是支持向量回归 ( SVR )。
用支持向量回归进行估计
顾名思义,SVR 是支持向量族的部分,是支持向量机 ( SVM )的同胞,用于分类(或者我们可以直接称之为 SVC ),您在第三章、使用支持向量机识别人脸。
概括地说,支持向量机寻求一个最佳超平面,它能最好地分离不同类别的观测值。假设超平面由斜率向量 w 和截距 b 确定,并且选择最佳超平面,使得从每个隔离空间中最近的点到超平面的距离(可以表示为)最大化。最优的 w 和 b 可以通过以下优化问题学习和求解:
- 最小化|| w ||
- 以y(I)(wx(I)+b)≥1 为条件,训练集为( x (1) 、 y (1) )、( x (2) 、 y )
在 SVR 中,我们的目标是找到一个决策超平面(由一个斜率向量 w 定义并截取 b )这样两个超平面 wx + b =- ε (负超平面)和wx+b=ε(正超平面)可以覆盖大部分训练数据。换句话说,大多数数据点被限制在最佳超平面的 ε 带中。同时,最优超平面越平坦越好,这意味着 w 越小越好,如下图所示:
图 7.11:在支持向量回归机中寻找决策超平面
这转化为通过解决以下优化问题来推导出最优 w 和 b :
- 最小化|| w ||
- 以|y(I)(wx(I)+b)|≤ε为条件,给定一套( x (1) 、 y (1) )、( x (2) 、 y
支持向量回归机背后的理论与 SVM 非常相似。在下一节中,让我们看看 SVR 的实现。
实现支持向量回归
再次,为了解决前面的优化问题,我们需要求助于二次规划技术,这超出了我们学习旅程的范围。因此,我们不详细介绍计算方法,将使用 scikit-learn 的SVR包(https://sci kit-learn . org/stable/modules/generated/sklearn . SVM . SVR . html)实现回归算法。
在 SVM 使用的重要技术,例如作为偏差和方差之间的权衡的惩罚,以及处理线性非分离的核(例如径向基函数),可以转移到支持向量回归机。scikit-learn 的SVR包也支持这些技术。
这次我们用SVR来解决之前的房价预测问题:
>>> from sklearn.svm import SVR
>>> regressor = SVR(C=0.1, epsilon=0.02, kernel='linear')
>>> regressor.fit(X_train, y_train)
>>> predictions = regressor.predict(X_test)
>>> print(predictions)
[ 14.59908201 19.32323741 21.16739294 18.53822876 20.1960847
23.74076575 22.65713954 26.98366295 25.75795682 22.69805145]
您已经学习了三(或四)种回归算法。那么,我们应该如何评价回归性能呢?让我们在下一节找到答案。
评估回归性能
到目前为止,我们已经深入介绍了三种流行的回归算法,并通过使用几个著名的库从头开始实现了它们。我们不需要通过打印预测来判断一个模型在测试集上的表现,而是需要用以下指标来评估它的性能,这些指标会给我们更好的见解:
-
正如我提到的,均方误差衡量的是对应于期望值的平方损失。有时平方根取在均方误差之上,以便将数值转换回被估计的目标变量的原始标度。这产生均方根误差 ( RMSE )。此外,由于我们首先计算误差的平方,RMSE 的好处是更能惩罚大误差。
-
The mean absolute error (MAE) on the other hand measures the absolute loss. It uses the same scale as the target variable and gives us an idea of how close the predictions are to the actual values.
对于均方误差和均方误差,数值越小,回归模型越好。
-
R 2 (发音为 r 平方)表示回归模型的拟合优度。回归模型能够解释的是因变量变化的分数。它的范围从 0 到 1,代表从不适合到完美的预测。R 2 有一个变体叫做调整后的 R,它相对于数据点的数量来调整模型中的特征数量。
让我们使用 scikit-learn 中的相应函数来计算线性回归模型上的这三个测量值:
-
我们将再次处理糖尿病数据集,并使用网格搜索技术
>>> diabetes = datasets.load_diabetes() >>> num_test = 30 # the last 30 samples as testing set >>> X_train = diabetes.data[:-num_test, :] >>> y_train = diabetes.target[:-num_test] >>> X_test = diabetes.data[-num_test:, :] >>> y_test = diabetes.target[-num_test:] >>> param_grid = { ... "alpha": [1e-07, 1e-06, 1e-05], ... "penalty": [None, "l2"], ... "eta0": [0.03, 0.05, 0.1], ... "max_iter": [500, 1000] ... } >>> from sklearn.model_selection import GridSearchCV >>> regressor = SGDRegressor(loss='squared_loss', learning_rate='constant', random_state=42) >>> grid_search = GridSearchCV(regressor, param_grid, cv=3)微调线性回归模型的参数
-
我们获得了最佳参数集:
>>> grid_search.fit(X_train, y_train) >>> print(grid_search.best_params_) {'alpha': 1e-07, 'eta0': 0.05, 'max_iter': 500, 'penalty': None} >>> regressor_best = grid_search.best_estimator_ -
我们用最优模型预测测试集:
>>> predictions = regressor_best.predict(X_test) -
我们基于 MSE、MAE 和 R 2 度量来评估测试集的性能:
>>> from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score >>> mean_squared_error(y_test, predictions) 1933.3953304460413 >>> mean_absolute_error(y_test, predictions) 35.48299900764652 >>> r2_score(y_test, predictions) 0.6247444629690868
现在你已经了解了三个(或者四个,你可以说是四个)常用且强大的回归算法和绩效评估指标,让我们利用它们来解决我们的股价预测问题。
用三种回归算法预测股票价格
以下是预测股价的步骤:
-
Earlier, we generated features based on data from 1988 to 2019, and we will now continue with constructing the training set with data from 1988 to 2018 and the testing set with data from 2019:
>>> data_raw = pd.read_csv('19880101_20191231.csv', index_col='Date') >>> data = generate_features(data_raw) >>> start_train = '1988-01-01' >>> end_train = '2018-12-31' >>> start_test = '2019-01-01' >>> end_test = '2019-12-31' >>> data_train = data.loc[start_train:end_train] >>> X_train = data_train.drop('close', axis=1).values >>> y_train = data_train['close'].values >>> print(X_train.shape) (7558, 37) >>> print(y_train.shape) (7558,)dataframe数据中除'close'外的所有字段都是特征列,'close'是目标列。我们有 7558 个训练样本,每个样本都是 37 维的。我们还有 251 个测试样本:>>> print(X_test.shape) (251, 37) -
我们将首先用基于 T4 的线性回归进行实验。在我们训练模型之前,您应该意识到基于 SGD 的算法对具有非常不同尺度的特征的数据是敏感的;例如,在我们的例子中,
open特征的平均值约为 8,856,而moving_avg_365特征的平均值约为 0.00037。因此,我们需要将特征标准化为相同或可比的比例。我们通过移除平均值并重新缩放到单位方差来实现:>>> from sklearn.preprocessing import StandardScaler >>> scaler = StandardScaler() -
我们使用由训练集
>>> X_scaled_train = scaler.fit_transform(X_train) >>> X_scaled_test = scaler.transform(X_test)教授的
scaler重新缩放两组 -
现在我们可以搜索具有最佳参数集的基于 SGD 的线性回归。我们指定
l2正则化和 1000 次迭代,调整正则化项乘数alpha和初始学习率eta0:>>> param_grid = { ... "alpha": [1e-4, 3e-4, 1e-3], ... "eta0": [0.01, 0.03, 0.1], ... } >>> lr = SGDRegressor(penalty='l2', max_iter=1000, random_state=42 ) >>> grid_search = GridSearchCV(lr, param_grid, cv=5, scoring='r2') >>> grid_search.fit(X_scaled_train, y_train) -
选择最佳线性回归模型,对测试样本进行预测:
>>> print(grid_search.best_params_) {'alpha': 0.0001, 'eta0': 0.03} >>> lr_best = grid_search.best_estimator_ >>> predictions_lr = lr_best.predict(X_scaled_test) -
Measure the prediction performance via the MSE, MAE, and R2:
>>> print(f'MSE: {mean_squared_error(y_test, predictions_lr):.3f}') MSE: 41631.128 >>> print(f'MAE: {mean_absolute_error(y_test, predictions_lr):.3f}') MAE: 154.989 >>> print(f'R^2: {r2_score(y_test, predictions_lr):.3f}') R^2: 0.964我们通过微调线性回归模型实现了
0.964的R2 。 -
Similarly, let's experiment with a random forest. We specify 100 trees to ensemble and tune the maximum depth of the tree,
max_depth; the minimum number of samples required to further split a node,min_samples_split; and the number of features used for each tree, as well as the following:>>> param_grid = { ... 'max_depth': [30, 50], ... 'min_samples_split': [2, 5, 10], ... 'min_samples_leaf': [3, 5] ... ... } >>> rf = RandomForestRegressor(n_estimators=100, n_jobs=-1, max_features='auto', random_state=42) >>> grid_search = GridSearchCV(rf, param_grid, cv=5, scoring='r2', n_jobs=-1) >>> grid_search.fit(X_train, y_train)请注意,这可能需要一段时间,因此我们使用所有可用的 CPU 内核进行训练。
-
选择最佳回归森林模型,对测试样本进行预测:
>>> print(grid_search.best_params_) {'max_depth': 30, 'min_samples_leaf': 3, 'min_samples_split': 2} >>> rf_best = grid_search.best_estimator_ >>> predictions_rf = rf_best.predict(X_test) -
Measure the prediction performance as follows:
>>> print(f'MSE: {mean_squared_error(y_test, predictions_rf):.3f}') MSE: 404310.522 >>> print(f'MAE: {mean_absolute_error(y_test, predictions_rf):.3f}') MAE: 419.398 >>> print(f'R^2: {r2_score(y_test, predictions_rf):.3f}') R^2: 0.6470.647的一个 R 2 是通过调整森林回归器获得的。 -
接下来,我们使用带有线性和 T4 径向基函数核的 T3 支持向量回归机,并保留罚超参数 T0 和 T1 以及径向基函数的核系数进行微调。与基于 SGD 的算法类似,支持向量回归在特征尺度不一致的数据上效果不佳:
```py
>>> param_grid = [
... {'kernel': ['linear'], 'C': [100, 300, 500],
'epsilon': [0.00003, 0.0001]},
... {'kernel': ['rbf'], 'gamma': [1e-3, 1e-4],
'C': [10, 100, 1000], 'epsilon': [0.00003, 0.0001]}
... ]
```
11. 同样,为了解决这个问题,我们使用重新缩放的数据来训练SVR模型:
```py
>>> svr = SVR()
>>> grid_search = GridSearchCV(svr, param_grid, cv=5, scoring='r2')
>>> grid_search.fit(X_scaled_train, y_train)
```
12. Select the best SVR model and make predictions of the testing samples:
```py
>>> print(grid_search.best_params_)
{'C': 500, 'epsilon': 0.0001, 'kernel': 'linear'}
>>> svr_best = grid_search.best_estimator_
>>> predictions_svr = svr_best.predict(X_scaled_test)
>>> print(f'MSE: {mean_squared_error(y_test, predictions_svr):.3f}')
MSE: 29999.827
>>> print(f'MAE: {mean_absolute_error(y_test, predictions_svr):.3f}')
MAE: 123.566
>>> print(f'R^2: {r2_score(y_test, predictions_svr):.3f}')
R^2: 0.974
```
借助支持向量回归机,我们能够在测试集上实现`0.974`的`R` <sup class="Superscript--PACKT-">2</sup> 。
13. 我们还绘制了由三种算法中的每一种生成的预测,以及基本事实:
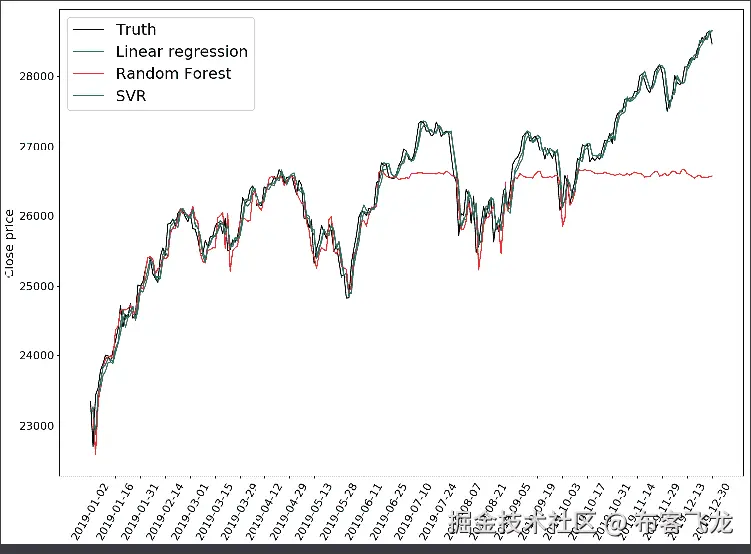
图 7.12:使用三种算法的预测与基本事实的对比
可视化由以下代码生成:
>>> import matplotlib.pyplot as plt
>>> plt.plot(data_test.index, y_test, c='k')
>>> plt.plot(data_test.index, predictions_lr, c='b')
>>> plt.plot(data_test.index, predictions_rf, c='r')
>>> plt.plot(data_test.index, predictions_svr, c='g')
>>> plt.xticks(range(0, 252, 10), rotation=60)
>>> plt.xlabel('Date')
>>> plt.ylabel('Close price')
>>> plt.legend(['Truth', 'Linear regression', 'Random Forest', 'SVR'])
>>> plt.show()
在本节中,我们分别使用三种回归算法构建了一个股票预测器。总的来说,SVR 优于其他两种算法。
摘要
在本章中,我们研究了本书的最后一个项目,使用机器学习回归技术预测股票(特别是股票指数)价格。我们首先简单介绍了股票市场和影响交易价格的因素。为了解决这个十亿美元的问题,我们研究了机器学习回归,它估计一个连续的目标变量,而不是分类中的离散输出。随后,我们深入讨论了三种流行的回归算法,线性回归、回归树和回归森林以及支持向量回归机。我们用几个流行的框架从头开始介绍了它们的定义、机制和实现,包括 scikit-learn 和 TensorFlow,以及在玩具数据集上的应用。您还学习了用于评估回归模型的指标。最后,我们应用本章所涵盖的内容来解决我们的股价预测问题。
在下一章中,我们将继续研究股价预测项目,但是使用强大的神经网络。我们将看看他们是否能击败我们在本章中使用三个回归模型所取得的成就。
练习
- 如前所述,你能给我们的股票预测系统增加更多的信号吗,比如其他主要指数的表现?这能提高预测吗?
- 回想一下,除了 DJIA,我还简单提到了几个主要的股指。考虑到这些主要指数的历史价格和表现,是否有可能对我们刚刚开发的 DJIA 价格预测模型进行改进?很有可能!这背后的想法是,没有股票或指数是孤立的,股票和不同金融市场之间有弱或强的影响。这应该是耐人寻味的探索。
- 能否尝试集成线性回归和 SVR,比如对预测进行平均,看看能否提高预测?