上一篇音乐基础和接下来一系列的噪声都是因为 www.shadertoy.com/view/4sSSWz 这一个 shader理解过程中不懂的地方而衍生出学习的地方。
2501192600
我其实还蛮享受这种漫无目的散射的学习，看到一个不懂的点钻进去折腾会儿。 本文探讨了数字生成技术中最重要的技术原理，如何通过计算机生成噪声。 也会基于 random 函数本质去理解如何实现上面的很多线的效果。
本文的主要参考资料在文尾给出
随机
以下是 shadertoy最长看到的一个 Random函数
float hash1(float n) { return fract(sin(n * 123.456) * 456.789);}
这里利用的原理是当 sin函数拉倒一个非常大的范围空间，其小数呈现了一定随机性。 例如当我们将 n 设置为 uv.x， 可以在屏幕中看到不同的条纹线
col = vec3(hash1(uv.x));
2501193146
利用同样的原理我们可扩展出如果面对一个 二维的 random函数，不过这里要先用一个 dot函数，可以让二维变成 一维
float hash2(vec2 n) { return fract(sin(dot(n, vec2(123.4, 567.8)) * 123.456) * 456.789);}
变得到这样一张雪花图
随机的一些问题
随机的问题主要有两点，一个是不够随机，一个是太随机了...
比如下面这个图片，在sin(pi) 的 sin(-pi)就出现了一些问题。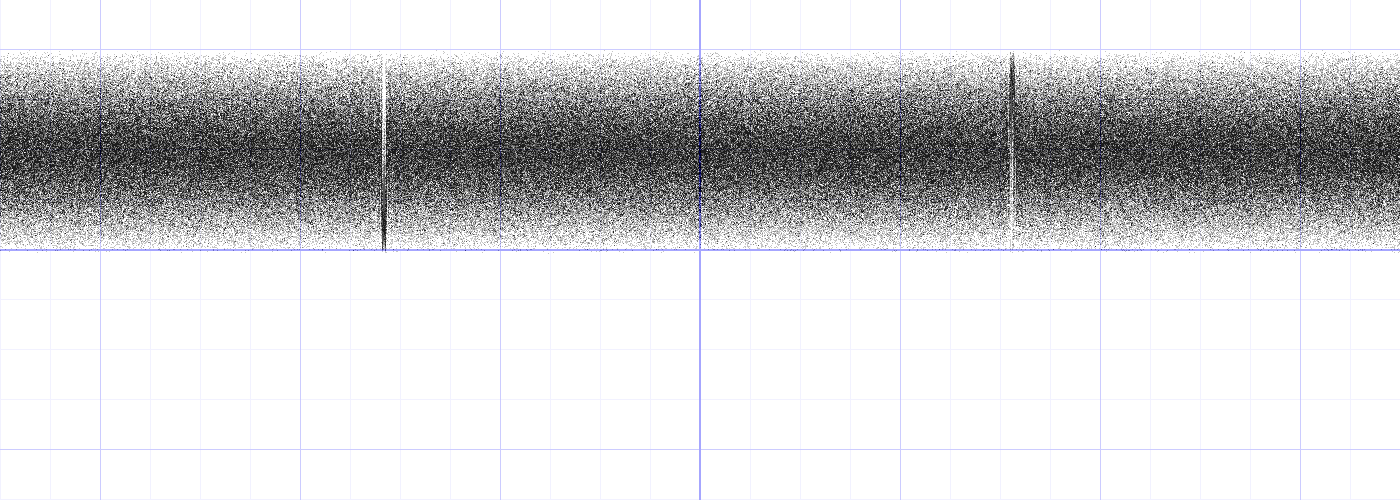 
所以在这篇文章中 pixelero.wordpress.com/2008/04/24/… 做了有趣的实验，js的 random函数并不是那么 random， 例如他在做 random的 3 次方，random的 sqrt，都会发现 random之后的分布并不符合概率统计。所以在设计 random函数的时候有时候会看到一些魔法数字，这都是经过设计者多次实验尝试出来的。建议不要改动....
再比如 sin函数在不同的 GPU下，当 sin某个特别大的值，例如 sin(123456. * x)，会在不同的 GPU获得不一致的结果。这会导致画面在不同机器渲染出现不一致情况，解决这个问题的思路也很简单，我们知道 两个向量的点乘是 向量长度与 cos(向量角度)的乘法， 也有了一个三角函数，同时也可以避免因为GPU sin精度问题， 例如lyria下的这个 hash22的函数
vec2 hash22(vec2 p){ vec3 p3 = fract(vec3(p.xyx) * vec3(.1031, .1030, .0973)); p3 += dot(p3, p3.yzx+33.33); return fract((p3.xx+p3.yz)*p3.zy);}
白噪声 White Noise
也被成为杂色噪声
我们常常听说白噪声，据说白噪声具有帮助屏蔽其他噪音的特性，因此常用于睡眠、集中注意力或放松的环境中。它可以掩盖其他不规则的声音，使人们能够更容易地入睡或提高工作效率。其特征是在整个可听频率范围内具有均匀的能量分布。换句话说，白噪声包含了所有频率的声音，这些声音的强度是均匀的，因此听起来像是一种“嘶嘶”的声音，类似于电视机未调频时的杂音。
为啥忽然说起这个呢... 因为根据上一篇将声音的基本原理，结合上面的 hash2， 我们就可以很快的做出白噪音...在回顾一下，震动产生波，多种震动产生多种波，波的叠加通过传导物质到耳膜变成电信号被我们听到。所以声音的是波的叠加，不同波有不同频率，如果各频率波振幅(响度)起起伏伏差不多，那就是白噪声。。。 其实也就是一个在某时某刻声音被采样就是一个随机值
#define ITERATIONS 8.0vec2 mainSound( in int samp,float time){ vec2 audio = vec2(0.0); for (float v = 0.0; v < ITERATIONS; v++) { audio += hash22(iSampleRate * vec2(time + v, time*1.423 + v)) * 2.0 - 1.0; } audio /= float(ITERATIONS); return audio*.1 ;}
将以上代码贴到 shadertoy就可以获得白噪声， 如果我们对 声音的响度做一个 波函数，可以调出一些类似雨声的感觉～～
随机函数生成多条线
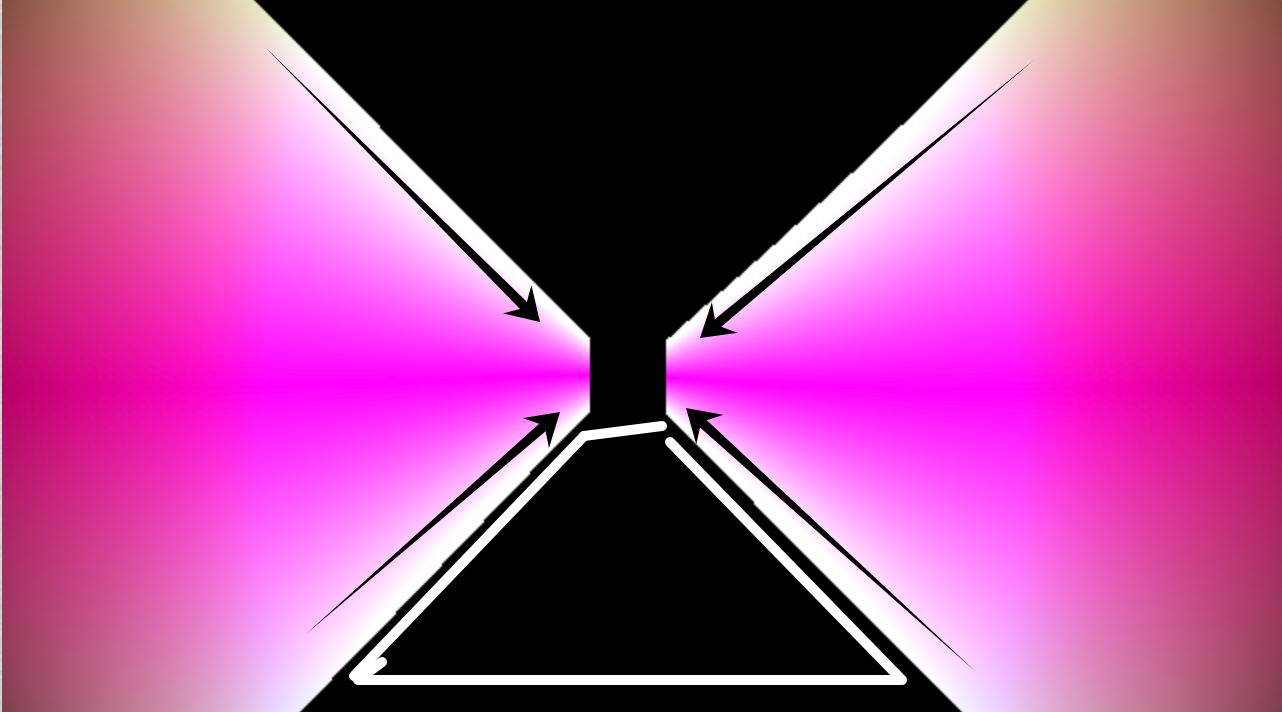
回到最开始的这个个 shader, 他是如何生成那么多线的呢。 这里简单说一下他主要的设计思路，可以这么理解，在视野的两侧有很多无线长的玻璃，每个玻璃会贴一些短胶带，
2501200313
我们单拿一个面出来看，每个面可以划分成多行， 这个很简单就是对 y进行放大在 fract
2501200729
void mainImage( out vec4 fragColor, in vec2 fragCoord ){ // Normalized pixel coordinates (from 0 to 1) vec2 uv = fragCoord/iResolution.xy * 2.0 - 1.0; uv.x *= iResolution.x/iResolution.y; uv.y *= 5.; uv.y = fract(uv.y); // Output to screen fragColor = vec4(vec3(uv.y),1.0);}
再进一步我们对不同的 行，根据 x做一个sin函数，同时也引入 y的 index也就是利用 x放大
float idx = floor(uv.y); float c = sin(uv.x * 24.567 + idx * 46.56 ); fragColor = vec4(vec3(c),1.0);
于是得到下面这张图片， 三角函数的周期性，负数就是黑的，正数就是白色。 这就是上面那个效果最基本的原理，当然坐着还使用了很多其他技巧，但最本质的，都是操作这些随机的小白块
资料
-
The art of code: Value Noise Explained
-
Metaverse大衍神君 随机与噪声 www.bilibili.com/video/BV16d…
-
The book of shader thebookofshaders.com/10/
