机器学习算法——逻辑回归逻辑回归是一种统计模型，用来解决分类问题，尤其是二分类问题。通过学习输入特征与输出标签之间的关系

逻辑回归是一种统计模型，用来解决分类问题，尤其是二分类问题。通过学习输入特征与输出标签之间的关系，来估计样本属于某一类别的概率。

逻辑回归模型通过逻辑函数将线性回归的输出映射为一个 0 到 1 之间的概率值，然后再将这个概率与提前设置的阈值进行比较，最终根据比较的结果来确定样本属于哪一个分类。

⒈ 逻辑函数

考虑一个场景：假设老师打算通过每个学生平时的学习时长来预测其考试成绩，可以通过建立线性回归模型，以学生的学习时长为特征 $x$ ，考试成绩为目标 $y$ ：

y = \beta_0 + \beta_1 \times x

但如果老师希望通过学习时长来预测学生通过考试的概率，此时线性回归已经无法满足要求，因为概率的值只能介于 $\left[0,1 \right]$ 之间。

几率

几率指的是一件事情成功的概率与失败的概率的比值，假设成功的概率为 $P$ ，则失败的概率为 $1 - P$ 。用几率替换线性回归模型中的目标：

\frac{P}{1-P} = \beta_0 + \beta_1 \times x

由于概率取值范围的限制，几率的取值只能介于 $\left[0,+\infty \right)$ 之间。但在实际应用中，线性回归的取值介于 $\left(- \infty, + \infty \right)$ 之间。为了修正二者取值范围的偏差，需要对几率取自然对数：

\ln\frac{P}{1-P} = \beta_0 + \beta_1 \times x

自然对数函数

我们最终要实现的是对概率 $P$ 的预测，所以我们需要通过上述等式最终推导出概率 $P$ 的函数表达式。将上述等式两边同时作为 $e$ 的指数，则有：

\frac{P}{1-P} = e^{\beta_0 + \beta_1 \times x}

P = \frac{e^{\beta_0 + \beta_1 \times x}}{1 + e^{\beta_0 + \beta_1 \times x}}

将函数表达式进行约分，最终得到逻辑函数（Signoid）表达式：

P = \frac{1}{1 + e^{-(\beta_0 + \beta_1 \times x)}}

逻辑函数图像

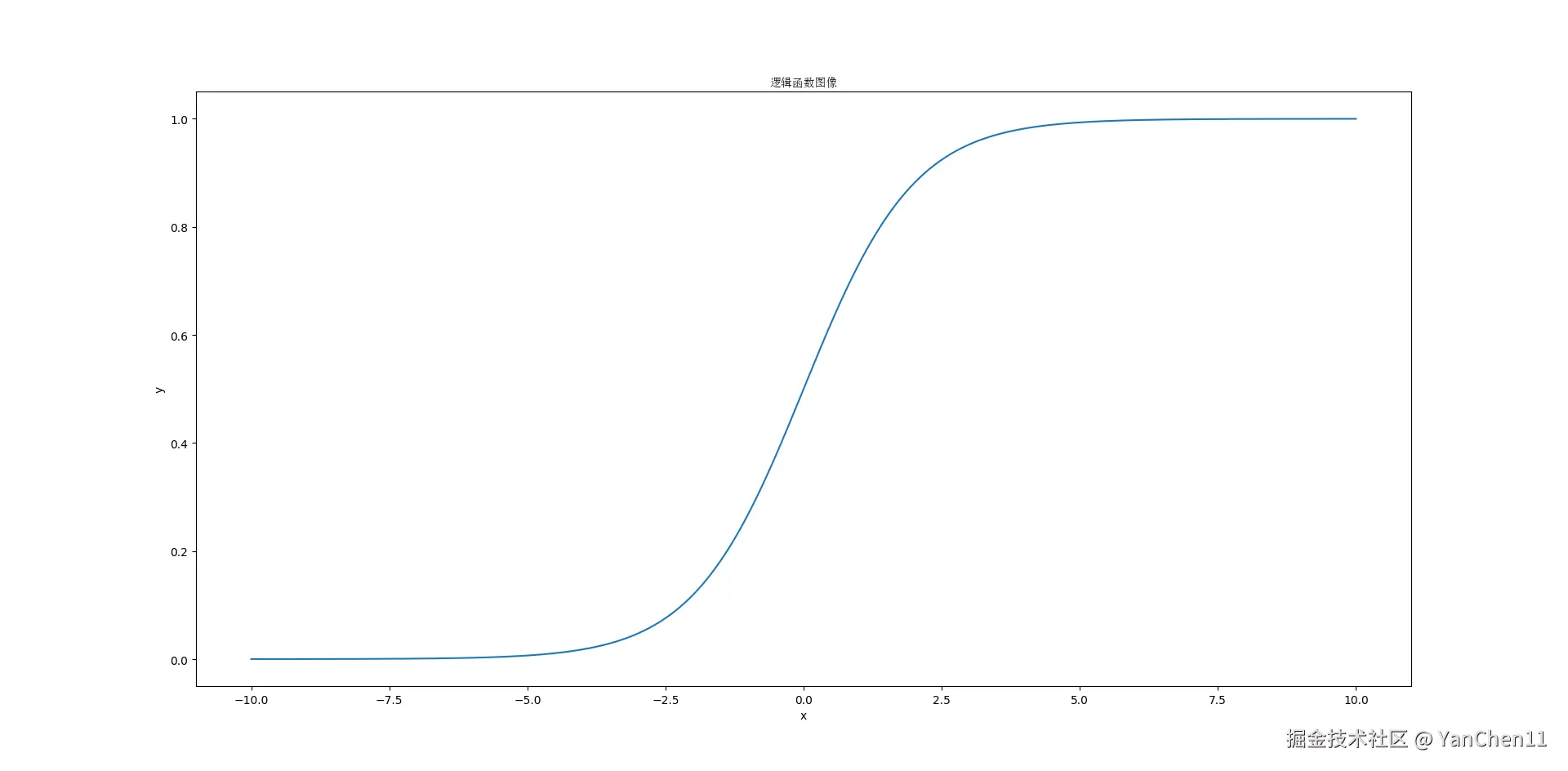
通过引入逻辑函数，能够将线性回归模型的输出转化为概率值，通过比较概率值与预先设置的阈值，从而处理二分类问题。逻辑函数是逻辑回归模型的核心，它确保了模型的输出始终在 $\left[0,1 \right]$ 之间，使得模型能够被解释为事件发生的概率。这也是逻辑回归在分类任务中如此广泛应用的原因。

假设

逻辑回归主要用来解决二分类问题，所以逻辑回归的输出结果必须是二元的，即只能有两个输出结果。如果输出结果多于两个，那么需要使用多分类或序数逻辑回归。
特征和几率的对数必须满足线性关系，这可以从上述逻辑函数的推导过程中得到验证。
样本中不能有异常值：异常值会影响线性回归的最佳拟合结果，从而影响逻辑回归的预测结果的准确性。
模型的特征之间不能有多重共线性，即特征之间不能有高度相关性，因为这会影响模型的稳定性。
样本之间应该相互独立。
样本的数量应该足够大，以保证模型的稳定性以及预测结果的可靠性。一个常见的经验法则是：每个独立的特征对应每个分类结果至少应该有 10 个样本。以二分类问题为例，每个特征至少应该有 10 个正样本，10 个负样本。如果模型有 5 个特征，那么至少需要 100 个样本。

⒉ 损失函数

在线性回归中，通常以均方误差（MSE）作为损失函数。由于均方误差是线性回归参数的凸函数，通过梯度下降我们可以最终找到线性回归参数的最优解。但在逻辑回归中，均方误差相对于逻辑回归的参数会存在多个局部最优解，所以逻辑回归中无法使用均方误差作为损失函数。

二分逻辑回归的 MSE 函数

上图为二分逻辑回归 $P = \frac{1}{1 + e^{-(\beta_0 + \beta_1 \times x)}}$ 的均方误差函数图像。图中，均方误差相对于逻辑回归参数 $\theta_0$ 和 $\theta_1$ 都有多个局部最优解，这种情况无法通过梯度下降找到逻辑回归参数的全局最优解。

最大似然估计

最大似然估计是一种预测模型参数的统计方法，其目的是合理的选择模型参数以使模型产生实际观测到的数据的可能性最大化。最大似然估计的第一步是假设数据的概率分布。

在逻辑回归中，最大似然估计的主要目的是确定使得似然函数最大化的模型的参数。这里的似然函数，指的是样本数据的概率密度函数。

伯努利分布

伯努利分布是一种只有两种可能的输出结果的离散分布，分别标记为 0 和 1。其中，结果为 0 的概率为 $p$ ，结果为 1 的概率为 $1 - p$ 。其概率密度函数为

P(n) = \begin{cases} p, & n = 0, \\ 1 - p, & n = 1 \end{cases}

也可以写成

P(n) = p^n*(1-p)^{1 - n}

其中， $n$ 的取值只能为 0 或 1。

二分逻辑回归也适用于伯努利分布的情况，并且由于二分逻辑回归中的样本之间相互独立，所以二分逻辑回归的似然函数为

L(\beta) = \prod_{i = 1}^{n}P(x_i)^{y_i}*(1 - P(x_i))^{1 - y_i}

其中， $P(x_i)$ 为第 $i$ 个样本的预测结果，即 Sigmoid 函数的结果； $y_i$ 为第 $i$ 个样本的实际分类。

对上述似然函数两边同时取自然对数，则有

\log(L(\beta)) = \sum_{i = 1}^{n}[y_i * \log P(x_i) + (1 - y_i) * \log (1 - P(x_i))]

其中， $P(x_i) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 * x_i)}}$ 。

梯度下降

我们的目的是求得使上述对数函数值最大化的模型参数 $\beta_0$ 和 $\beta_1$ 的值。在机器学习中，我们通常可以通过梯度下降来求得损失函数的最小值，为了使梯度下降得以应用，我们需要对上述对数函数进行适当的变形。

在对数运算中， $-\log x = \log x^{-1} = \log \frac{1}{x}$ 。所以，我们可以通过求解 $- \log(L(\beta))$ 的最小值来变相的求解 $\log(L(beta))$ 的最大值。另外，为便于计算，通常会对整个样本集取平均，所以最终的损失函数为

\begin{align} J(\beta) & = -\frac{1}{n} \sum_{i = 1}^{n}[y_i * \log P(x_i) + (1 - y_i) * \log (1 - P(x_i))] \\ P(x_i) & = \frac{1}{1 + e^{-z}} \\ z & = \beta_0 + \beta_1 * x \end{align}

求解损失函数对 $\beta$ 的偏导数，根据求导法则

\frac{\partial J(\beta)}{\partial \beta} = \frac{\partial J(\beta)}{\partial P} \times \frac{\partial P}{\partial z} \times \frac{\partial z}{\partial \beta}

我们首先对样本集中的一个样本的情况进行求导

\begin{align} \frac{\partial J(\beta)}{\partial P} & = - (\frac{y}{P} + \frac{1 - y}{1 - P} \times (-1)) \\ \frac{\partial P}{\partial z} & = \frac{\partial}{\partial z}\left(\frac{1}{1 + e^{-z}}\right) \\ & = \frac{\partial}{\partial z}(1 + e^{-z})^{-1} \\ & = -1 \times (1 + e^{-z})^{-2} \times \frac{\partial}{\partial z}(1 + e^{-z}) \\ & = -1 \times (1 + e^{-z})^{-2} \times (0 + \frac{\partial}{\partial z}e^{-z}) \\ & = -1 \times (1 + e^{-z})^{-2} \times (e^{-z} \times \frac{\partial}{\partial z}(-z)) \\ & = -1 \times (1 + e^{-z})^{-2} \times e^{-z} \times (-1) \\ & = \frac{e^{-z} + 1 - 1}{(1 + e^{-z})^2} \\ & = \frac{1}{1 + e^{-z}} \times (1 - \frac{1}{1 + e^{-z}}) \\ & = P \times (1 - P) \\ \frac{\partial z}{\partial \beta} & = x \end{align}

最终，单个样本的求导结果为

\begin{align} \frac{\partial J(\beta)}{\partial \beta} & = -(\frac{y}{P} - \frac{1 - y}{1 - P}) \times P \times (1 - P) \times x \\ & = -[y(1 - P) - P(1 - y)] \times x \\ & = (P - y) \times x \end{align}

所以，对整个样本集的求导结果，即损失函数的梯度为

\frac{\partial J(\beta)}{\partial \beta_j} = \frac{1}{n} \sum_{i = 1}^n(P_i - y_i)x_{ij}

其中， $P_i$ 和 $y_i$ 分别为第 $i$ 个样本的预测值和实际值，而 $x_{ij}$ 为第 $i$ 个样本的第 $j$ 个特征， $\beta_j$ 为第 $j$ 个特征的参数。

梯度下降过程中，更新梯度的公式为

\beta_j = \beta_j - \alpha \frac{1}{n} \sum_{i = 1}^n(P_i - y_i)x_{ij}

其中 $\alpha$ 为学习率。

⒊ 评估指标

逻辑回归模型在训练完之后，需要对模型的性能进行评估。常用的评估逻辑回归模型的指标有

准确率（accuracy）
精确率（precision）
召回率（recall）
F1 分数（F1 score）

在计算逻辑回归模型指标的过程中需要用到以下参数：

TP（True Positive）：实际为正样本，预测结果也为正样本的数量
TN（True Negative）：实际为负样本，预测结果也为负样本的数量
FP（False Positive）：实际为负样本，但预测结果为正样本的数量
FN（False Negative）：实际为正样本，但预测结果为负样本的数量

准确率

准确率指的是预测正确的样本数量占总样本数量的比例，既包括 TN，也包括 TF。准确率的计算公式为

Accuracy = \frac{TN + TP}{TN + TP + FN + FP}

准确率虽然容易理解，但如果样本类别存在倾斜，那么准确率的结果可能会产生误导，无法正确体现模型的性能。例如，样本中的大多数样本均为正样本或负样本，那么即使有少量样本预测错误，整体的准确率也会比较高。

精确率

精确率指的是被模型预测为正样本的样本中，实际为正样本的样本数的占比。精确率的计算公式为

Precision = \frac{TP}{TP + FP}

精确率关注的是预测为正样本的样本中实际为正样本的样本数，所以通常用于关注假阳的情况。

召回率

召回率指的是实际为正样本的样本中，被正确的预测为正样本的样本的占比。召回率的计算公式为

Recall = \frac{TP}{TP + FN}

召回率关注的是实际的正样本中有多少被成功的预测为正样本，所以通常用于关注假阴的情况。

F1 分数

F1 分数是精确率和召回率的调和平均数，可以同时兼顾假阳和假阴的情况。F1 分数的计算公式为

f1 = 2 \times \frac{Precision \times Recall}{Precison + Recall}