试着推导一下Linux中计算Load Average的算式

参考：www.fortra.com/resources/g…

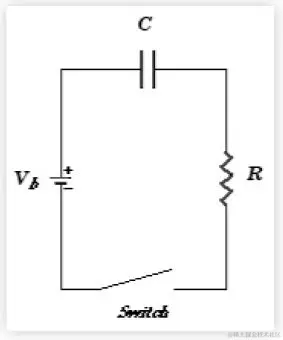
对于这个RC电路，根据串联电路的电压关系，

(1)

V_b = V_C + V_R

又因为

(2)

V_C = \frac {1} {C}q

(3)

V_R = RI

将(2)、(3)代入(1)，并整理，得到

(4)

RI = -\frac {1} {C}q + V_b

两边同时乘以 $C$

(5)

RIC = -q+CV_b

考虑 $t$ 时刻的瞬时电流

(6)，

I(t) = \frac {dq(t)} {dt}

将(6)代入(5)，并整理

(7)

RC(\frac {dq(t)} {dt}) = -q(t) + CV_b(t)

解微分方程(7)，得到

(8)

q(t) = e^{-\frac {t+c} {RC}} + CV_b(t)

忽略常数项 $c$

(9)

q(t) = e^{-\frac {t} {RC}} + CV_b(t)

考虑 $(t-\Delta t)$ 时刻的状态

(10)

q(t-\Delta t) = e^{-\frac {t-\Delta t} {RC}} + CV_b(t-\Delta t)

(10)两端同时乘以下面这个因数

(11)

e^{-\frac {\Delta t} {RC}}

(12)

e^{-\frac {\Delta t} {RC}} q(t-\Delta t) = e^{-\frac {\Delta t} {RC}} e^{-\frac {t-\Delta t} {RC}} + e^{-\frac {\Delta t} {RC}} CV_b(t-\Delta t)

化简(12)

(13)

e^{-\frac {\Delta t} {RC}} q(t-\Delta t) = e^{-\frac {\Delta t} {RC} - \frac {t-\Delta t} {RC}} + e^{-\frac {\Delta t} {RC}} CV_b(t-\Delta t)

(14)

e^{-\frac {\Delta t} {RC}} q(t-\Delta t) = e^{-\frac {t} {RC}} + e^{-\frac {\Delta t} {RC}} CV_b(t-\Delta t)

带入(9)，并整理

(14)

e^{-\frac {\Delta t} {RC}} q(t-\Delta t) = q(t) - CV_b(t) + e^{-\frac {\Delta t} {RC}} CV_b(t-\Delta t)

(15)

q(t) = e^{-\frac {\Delta t} {RC}} q(t-\Delta t) + CV_b(t) - e^{-\frac {\Delta t} {RC}} CV_b(t-\Delta t)

假设在很短的 $\Delta t$ 时间内， $V_b(t) = V_b(t-\Delta t) = V_b$ ，则

(17)

q(t) = e^{-\frac {\Delta t} {RC}} q(t-\Delta t) + (1 - e^{-\frac {\Delta t} {RC}}) CV_b

而Linux的Load Average为

avenrun[t] = avenrun[t-Δt] * exp + nr_active * (1 - exp)

其中，

q(t) = avenrun[t] -> run queue length
exp = e^(-Δt/RC) -> weight
nr_active = CV_b -> current active processes

The sampled value of the electric charge (q(t)) at time step (t) corresponds to the sampled run-queue length, q(t-Δt) is the previous sample of the run-queue, and the amount of charge remaining in the capacitor represents the number of active processes (CV_b).