《Fundamentals of Computer Graphics》第五版 第十四章 PBR

濠水之鱼
180 阅读10分钟

PBR（Physics-Based Rendering，基于物理的渲染）是严格遵从物理模型——而不是使用唯象公式——来渲染。

光的反射、折射与吸收

辐射可用大量光子来描述。与物理学不同，图形学中所说的光子只是一个遵从几何光学规律的能量波包。光子有它的位置、传播方向、波长 λ\lambda、光速 cc、频率 f=c/λf=c/\lambda 和能量 q=hf=hc/λq=hf=hc/\lambda，其中 h=6.63×10−34J⋅sh=6.63\times 10^{-34}\mathrm{J\cdot s} 是普朗克常数。这些属性中，光速依赖于介质的折射率，而频率和能量在传播过程中一般不会发生变化。

光在介质界面处会发生反射和折射，光的折射遵从斯涅耳定律（Snell's law）：

nisin⁡θ=ntsin⁡ϕn_{i}\sin\theta = n_{t}\sin\phi

其中，θ\theta、ϕ\phi 是入射角和折射角，nin_{i}、ntn_{t} 是两介质的折射率（refractive index）。反射光和折射光的方向向量为：

r⃗=d⃗−2(d⃗⋅n⃗)n⃗t⃗=ni[d⃗−(d⃗⋅n⃗)n⃗]nt−n⃗1−ni2[1−(d⃗⋅n⃗)2]nt2\begin{aligned} \vec{r} &= \vec{d} - 2(\vec{d}\cdot\vec{n})\vec{n} \\ \vec{t} &= \frac{n_{i}\left[\vec{d} - (\vec{d}\cdot\vec{n})\vec{n}\right]}{n_{t}} - \vec{n}\sqrt{1 - \frac{n_{i}^{2}\left[1 - (\vec{d}\cdot\vec{n})^{2}\right]}{n_{t}^{2}}} \end{aligned}

上式中被开方数为负时，透射（折射）光的能量为零，光被全反射（total internal reflection）。

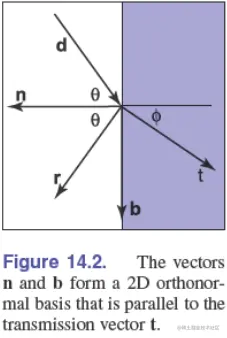
reflection-refraction.png

反射光和折射光的电场强度由菲涅耳公式（Fresnel equations）决定：

Er⊥Ei⊥=nicos⁡θ−ntcos⁡ϕnicos⁡θ+ntcos⁡ϕEt⊥Ei⊥=2nicos⁡θnicos⁡θ+ntcos⁡ϕEr∥Ei∥=ntcos⁡θ−nicos⁡ϕntcos⁡θ+nicos⁡ϕEt∥Ei∥=2nicos⁡θntcos⁡θ+nicos⁡ϕ\begin{aligned} \frac{E_{r\perp}}{E_{i\perp}} &= \frac{n_{i}\cos\theta - n_{t}\cos\phi}{n_{i}\cos\theta + n_{t}\cos\phi} \\ \frac{E_{t\perp}}{E_{i\perp}} &= \frac{2n_{i}\cos\theta}{n_{i}\cos\theta + n_{t}\cos\phi} \\ \frac{E_{r\parallel}}{E_{i\parallel}} &= \frac{n_{t}\cos\theta - n_{i}\cos\phi}{n_{t}\cos\theta + n_{i}\cos\phi} \\ \frac{E_{t\parallel}}{E_{i\parallel}} &= \frac{2n_{i}\cos\theta}{n_{t}\cos\theta + n_{i}\cos\phi} \end{aligned}

其中，下标 ⊥\perp、∥\parallel 分别表示与入射面垂直、平行的方向，下标 ii、rr、tt 分别表示入射、反射和透射（折射）。图形程序中一般不考虑偏振，并使用 Schlick 发展的菲涅耳公式的近似版本来计算反射率：

R(θ,λ)=R0(λ)+[1−R0(λ)](1−cos⁡θ)5R(\theta, \lambda) = R_{0}(\lambda) + [1 - R_{0}(\lambda)](1 - \cos\theta)^{5}

其中，R0(λ)R_{0}(\lambda) 是法向反射率。

反射率是光强之比，反射系数是电场强度之比。

对于电介质界面：

R0(λ)=[nt(λ)−ni(λ)nt(λ)+ni(λ)]2R_{0}(\lambda) = \left[\frac{n_{t}(\lambda) - n_{i}(\lambda)}{n_{t}(\lambda) + n_{i}(\lambda)}\right]^{2}

对于金属，由于趋肤效应，光只能渗透到表面薄层，而无法进入金属内部。由于金属内部的自由电子会耗散掉透射波的能量，因此，金属的折射率为复数，电磁波耗散（电导率）导致了虚部的产生，而折射率的实部以及折射角仍满足折射定律，采用复折射率，光在金属界面的反射仍满足菲涅耳公式。

电导率也会影响金属折射率的实部。

光在含有均匀杂质的介质中传播时，光强的衰减服从比尔定律（Beer’s Law）：dI=−CIdxdI=-CIdx。据此可以解出：

I(s)=I(0)asI(s) = I(0)a^{s}

其中，aa 是单位距离 RGB 光强衰减常数，用于描述衰减程度，ss 是到界面的距离。

total-reflection.png

次表面散射（Subsurface Scattering）电介质

不透明介质可以使用多种电介质来模拟，比如在立方体冰块中加入许多的球形小气泡。另一种方法是将表面粗糙化，比如对曲面细分再对顶点做随机扰动。也可以插入一些有色粒子，并引入比尔定律，这种做法可用于模拟染料。许多复杂材料都可以使用显式的微结构来模拟，比如皮肤、染料粒子、血液等。

暴力光子追踪

传感器

图像捕获设备可以是一个由简单的传感器阵列和一个带有小孔的盒子构成的针孔相机。阵列中的每个传感器本质上就是一个光子计数器。为了生成彩色图像，可以在传感器前面放置红、绿、蓝滤波片，最简单的是带通滤波片（bandpass filter）：

  • 蓝色，只在 λ∈[400,500 nm]\lambda\in[400,500\ \text{nm}] 波段全响应。
  • 绿色，只在 λ∈[500,600 nm]\lambda\in[500,600\ \text{nm}] 波段全响应。
  • 红色，只在 λ∈[600,700 nm]\lambda\in[600,700\ \text{nm}] 波段全响应。

全响应就是当光子打到传感器上时，计数器加一。

光子追踪器（Photon Tracer）

追踪一个光子，需要先在光源处随机选择一个点，然后随机选择一个方向，再随机选择一个 400 nm400\ \text{nm} 到 700 nm700\ \text{nm} 之间的波长。接下来就可以对光线进行追踪，当打到一个物体表面时，计算反射率 RR，决定反射还是折射：

if (ξ<R)generate a reflection photon (ray) and trace itelsegenerate a refraction photon (ray) and trace it\begin{aligned} &\text{if}\ (\xi < R) \\ &\quad\text{generate a reflection photon (ray) and trace it} \\ &\text{else} \\ &\quad\text{generate a refraction photon (ray) and trace it} \end{aligned}

其中，ξ\xi 是一个标准随机数。如果是金属界面，折射光子将直接被吸收，因而重新生成一个新的光子。当光子进入到一个有吸收率的电介质时：

if (ξ<probability of absorption)absorb and start new photonelseallow this photon to exit medium at the next hit\begin{aligned} &\text{if}\ (\xi < \text{probability of absorption}) \\ &\quad\text{absorb and start new photon} \\ &\text{else} \\ &\quad\text{allow this photon to exit medium at the next hit} \end{aligned}

运动模糊（Motion Blur）和散焦模糊（Defocus Blur）

用透镜代替小孔可以让更多光子被记录下来。可以使用一套真实的复合玻璃透镜，也可以直接使用一个理想薄透镜。

最简单的玻璃透镜是两个球面组成的双凸球面透镜（bi-convex spherical lens）。虽然不如真实相机中的复合透镜，但也具有良好的成像性质，而且很容易做射线求交。

理想薄透镜是无限薄的，可以用半径和焦距 ff 来表示。以下三条性质可实现理想薄透镜：

  1. 一条从点 p⃗\vec{p} 穿过透镜中心的射线（p⃗\vec{p} 的中心线）不会弯曲；
  2. 点 p⃗\vec{p} 发出的所有通过透镜的光线都会汇聚到中心线上的点 q⃗\vec{q}；
  3. 物点 p⃗\vec{p} 沿着透镜光轴（optical axis）的距离 aa 和像点 q⃗\vec{q} 沿着透镜光轴的距离 bb 满足高斯公式 1/a+1/b=1/f1/a+1/b=1/f。

真实或理想透镜会自动产生真实图像中的模糊效果，也称为散焦模糊（defocus blur）或者景深（depth of field）——物方空间中能够清晰成像的前后范围。

当物体和相机存在相对运动时，相片中出现的模糊称为运动模糊（motion blur）。下面两个条件可以自动产生运动模糊：

  • 光源在相机的曝光时间内，在随机的时间点发射光子。
  • 射线追踪器有运动物体的概念，射线求交可接收时间为参数。

时间反演

即使使用了透镜，大部分光子还是无法被收集起来，从而导致上述光子追踪器的效率很低。图形学中通常从每个像素发射伴随光子（adjoint photon），当击中光源时就记录下来。光子的波长由滤波片对应的发光曲线（light emission curve）来决定。当击中光源时，就以发射光加权把光子记录在像素传感器阵列上。

辐射度量（Radiometry）

图形学中经常使用谱能量（spectral energy）Q=Δq/ΔλQ=\Delta q/\Delta\lambda——单位波长中所包含的光能，而不是能量本身。谱能量是一个强度量。对于谱能量的理解有两种方式：

  1. Δλ\Delta\lambda 足够小，但又足够大，以展示光的量子效应；
  2. 假定光是连续的，而非单个光子。

单位时间内产生的能量称为功率（power）。假定灯泡功率为 100W100\text{W}，发出的光波长为 500nm500\text{nm}，则可以计算 1s1\text{s} 时间内发出的光子数为 102010^{20}，这便是直接模拟光子效率很低的原因。实际上，和能量一样，图形学中更关心谱功率（spectral power）Φ=Δq/(ΔtΔλ)\Phi=\Delta q/(\Delta t\Delta\lambda)，它的值通常小于功率本身，这在调试时值得注意。

打到单位面积上的光功率称为辐照度（irradiance）。谱辐照度（spectral irradiance）定义为：

H=ΔqΔAΔtΔλH = \frac{\Delta q}{\Delta A\Delta t\Delta\lambda}

如果光是从曲面出射的，则称为辐出度（radiant exitance）EE。

辐亮度

图形程序中通常计算的是辐亮度（radiance）——单位立体角内的辐照度。谱辐亮度（spectral radiance）：

L=ΔHΔσ=ΔqΔAΔσΔtΔλ\begin{aligned} L &= \frac{\Delta H}{\Delta\sigma} \\ &= \frac{\Delta q}{\Delta A\Delta\sigma\Delta t\Delta\lambda} \end{aligned}

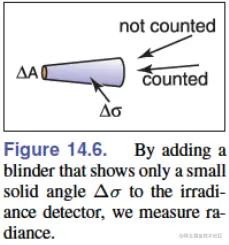
radiance.png

辐亮度的一个特性是，沿着探测方向移动不会发生变化。原因是，探测面积正比于探测距离的平方，而接收到的光反比于距离的平方，因此，辐亮度 L∝Δσd2/d2=ΔσL\propto\Delta\sigma d^{2}/d^{2}=\Delta\sigma 与探测距离无关。

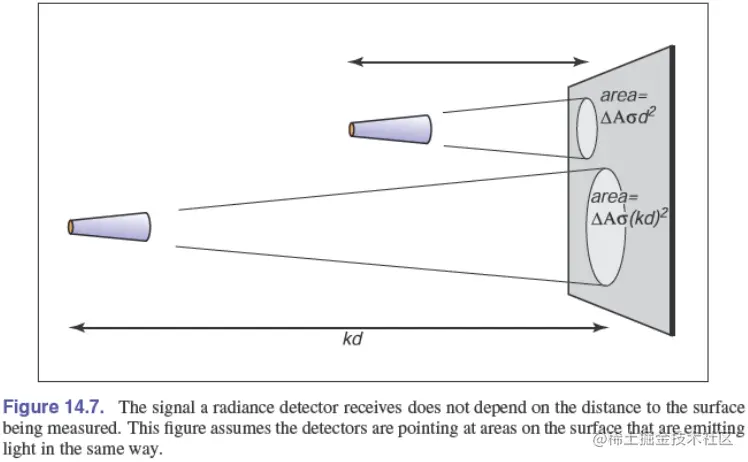
radiance-distance.png

如果观测面法向与观测方向夹角为 θ\theta，则谱辐亮度为：

L=ΔHΔσcos⁡θ=ΔqΔAcos⁡θΔσΔtΔλ\begin{aligned} L &= \frac{\Delta H}{\Delta\sigma\cos\theta} \\ &= \frac{\Delta q}{\Delta A\cos\theta\Delta\sigma\Delta t\Delta\lambda} \end{aligned}

曲面的出射辐亮度称为表面辐亮度（surface radiance）：

Ls=ΔEΔσcos⁡θL_{s} = \frac{\Delta E}{\Delta\sigma\cos\theta}

入射辐亮度称为场辐亮度（field radiance）：

Lf=ΔHΔσcos⁡θL_{f} = \frac{\Delta H}{\Delta\sigma\cos\theta}

所有其它的辐射物理量都可以用辐亮度表示。比如辐照度：

H=∫k⃗Lf(k⃗)cos⁡θ dσH = \int_{\vec{k}}L_{f}(\vec{k})\cos\theta\ d\sigma

Lf(k⃗)L_{f}(\vec{k}) 是沿着方向 k⃗\vec{k} 的辐亮度。

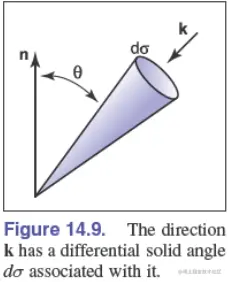
differential-solid-angle.png

照射到物体表面的光功率为：

Φ=∫x⃗H(x⃗)dA\Phi = \int_{\vec{x}}H(\vec{x})dA

散射、渲染方程

真实物体表面有很多精细结构，实际操作中并不会为这些精细结构建模，而是模拟出类似的效果。粗糙表面可以用一个在各方向上随机反射光的光滑表面来模拟，光在物体表面的随机反射由双向反射分布函数（bidirectional reflectance distribution function，简称 BRDF）来描述。类似地，光在物体内部的散射也可以通过建立一个统计模型来模拟，该模型刻画了光在任何一个位置上反射和吸收的可能性，以及散射光的方向分布，该分布称为相函数（phase function）。光在物体内部的散射由相函数来描述。

双向反射分布函数（bidirectional reflectance distribution function，简称 BRDF）定义为：

ρ(k⃗i,k⃗o)=LsH\rho(\vec{k}_{i}, \vec{k}_{o}) = \frac{L_{s}}{H}

其中，k⃗i\vec{k}_{i}、k⃗o\vec{k}_{o} 是光打到物体表面的入射和出射方向，HH 是 k⃗i\vec{k}_{i} 方向的光在物体表面的辐照度，LsL_{s} 是沿 kok_{o} 方向的表面辐亮度。

给定光的入射方向 k⃗i\vec{k}_{i}，光在物体表面的整体反射率称为定向半球反射率（directional hemispherical reflectance）：

R(k⃗i)=Power in all outgoing directions k⃗oPower in a beam from direction k⃗i=EH=∫k⃗oρ(k⃗i,k⃗o)cos⁡θo dσo\begin{aligned} R(\vec{k}_{i}) &= \frac{\text{Power in all outgoing directions $\vec{k}_{o}$}}{\text{Power in a beam from direction $\vec{k}_{i}$}} \\ &= \frac{E}{H} \\ &= \int_{\vec{k}_{o}}\rho(\vec{k}_{i}, \vec{k}_{o})\cos\theta_{o}\ d\sigma_{o} \end{aligned}

理想漫反射表面称为兰伯特表面（Lambertian surface），它的 BRDF 是一个不依赖角度的常数 ρ\rho，容易计算 R(k⃗i)=πρR(\vec{k}_{i})=\pi\rho。

渲染方程

根据 BRDF 定义可以得到渲染方程（rendering equation）：

Ls(k⃗o)=∫k⃗iρ(k⃗i,k⃗o)Lf(k⃗i)cos⁡θi dσiL_{s}(\vec{k}_{o}) = \int_{\vec{k}_{i}}\rho(\vec{k}_{i}, \vec{k}_{o})L_{f}(\vec{k}_{i})\cos\theta_{i}\ d\sigma_{i}

该方程也称为传输方程（transport equation），由 Kajiya 于 1986 年提出，并最早由 Immel、Cohen 和 Greenberg 写为上述形式。

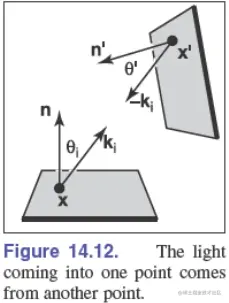
rendering-equation.png

由于发射方的表面辐亮度与接收方的场辐亮度相等 Ls(−k⃗i)=Lf(k⃗i)L_{s}(-\vec{k}_{i})=L_{f}(\vec{k}_{i})，因此渲染方程可写为如下的表面辐亮度形式：

Ls(x⃗,k⃗o)=∫x⃗′ visible to x⃗ρ(k⃗i,k⃗o)Ls(x⃗′,x⃗−x⃗′)cos⁡θicos⁡θ′∥x⃗−x⃗′∥2dA′=∫x⃗′ρ(k⃗i,k⃗o)Ls(x⃗′,x⃗−x⃗′)ν(x⃗,x⃗′)cos⁡θicos⁡θ′∥x⃗−x⃗′∥2dA′\begin{aligned} L_{s}(\vec{x}, \vec{k}_{o}) &= \int_{\vec{x}'\ \text{visible to}\ \vec{x}}\frac{\rho(\vec{k}_{i}, \vec{k}_{o})L_{s}(\vec{x}', \vec{x} - \vec{x}')\cos\theta_{i}\cos\theta'}{\|\vec{x} - \vec{x}'\|^{2}}dA' \\ &= \int_{\vec{x}'}\frac{\rho(\vec{k}_{i}, \vec{k}_{o})L_{s}(\vec{x}', \vec{x} - \vec{x}')\nu(\vec{x}, \vec{x}')\cos\theta_{i}\cos\theta'}{\|\vec{x} - \vec{x}'\|^{2}}dA' \\ \end{aligned}

上式被积函数中的表面辐亮度 LsL_{s} 使用了非归一化向量 x⃗−x⃗′\vec{x}-\vec{x}' 来表示从 x⃗′\vec{x}' 到 x⃗\vec{x} 的方向。

其中，ν\nu 是可见性函数（visibility function）：

ν(x⃗,x⃗′)={1if x⃗ and x⃗′ are mutually visible0otherwise\nu(\vec{x}, \vec{x}') = \left\{ \begin{aligned} &1 &&\text{if $\vec{x}$ and $\vec{x}'$ are mutually visible} \\ &0 &&\text{otherwise} \end{aligned} \right.

材质

对于那些能够影响宏观外观的微结构，在正常观测距离下，如果可以看到，则一般归属于几何模型；如果看不到，才会归属于物体材质。

BRDF 模型应用于诸多领域：遥感、传热、材料学、计算机图形学等，但没有一套标准术语，而大多数人对下图中的术语的理解是一致的：

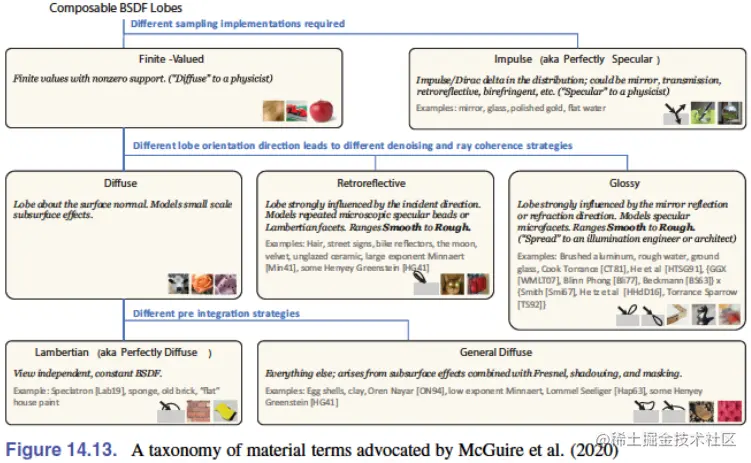
material-terms.png

工业生产中已经对材质进行了分类，并且有相应的 BRDF 模型，这些模型会进一步和 Fresnel/Schlick 公式的变形结合起来。实践中使用 Burley/Disney 模型的变种作为通用术语的越来越多，除了上图中的每个大类之外，它还包含了一个大类：辉光（sheen），用于表示类似边缘光照（rim lighting）的掠入射效应。retro-reflective（反光）在图形学中并不常用。

BRDF 模型中使用的最普遍的两个术语是漫反射（diffuse）和光泽（glossy）。diffuse 可以是常数，也可以有其它变形，比如在掠入射时变得更暗。目前 glossy 最主流的形式是 GGX 微平面（GGX microfacet），它需要找到微平面法向量的统计分布。

蒙特卡罗射线追踪（Monte Carlo Ray Tracing）

根据渲染方程，表面辐亮度可以用蒙特卡罗方法近似为：

Ls(k⃗o)≈ρ(q⃗,k⃗o)Lf(q⃗)cos⁡θip(q⃗)L_{s}(\vec{k}_{o}) \approx \frac{\rho(\vec{q}, \vec{k}_{o})L_{f}(\vec{q})\cos\theta_{i}}{p(\vec{q})}

其中，q⃗\vec{q} 是服从分布 pp 的随机数。入射方向场辐亮度 LfL_{f} 可以递归地应用蒙特卡罗积分来得到：

function rgb radiance(o⃗,d⃗)if ray o⃗+td⃗ hits something thenp⃗=hit pointq⃗=random directionreturn emitted(p⃗)+[ρ(q⃗,−d⃗)cos⁡θi/p(q⃗)]∗radiance(p⃗,q⃗)elsereturn background(o⃗,d⃗)\begin{aligned} &\text{function}\ \text{rgb radiance}(\vec{o}, \vec{d}) \\ &\quad\begin{aligned} &\textbf{if}\ \text{ray}\ \vec{o}+t\vec{d}\ \text{hits something}\ \textbf{then} \\ &\quad\begin{aligned} &\vec{p} = \text{hit point} \\ &\vec{q} = \text{random direction} \\ &\textbf{return}\ \text{emitted}(\vec{p}) + [\rho(\vec{q}, -\vec{d})\cos\theta_{i}/p(\vec{q})] * \text{radiance}(\vec{p}, \vec{q}) \end{aligned} \\ &\textbf{else} \\ &\quad\textbf{return}\ \text{background}(\vec{o}, \vec{d}) \end{aligned} \end{aligned}

这里所实现的函数 L(o⃗,d⃗)L(\vec{o}, \vec{d}) 用于计算来自方向 d⃗\vec{d} 的、带有自发光的点 p⃗\vec{p} 上的颜色。为避免无限递归，可能还需要提前终止 radiance\text{radiance} 函数。环境光 background\text{background} 可以设置为常数，也可以从环境映射（environment map）中查找，或是用其它方式生成。

光源很小时，上述算法可能会出现很多噪声，因为 emitted\text{emitted} 函数的值可能很大而且很稀少。实践中，通常单独计算发光物体的贡献来拆出直接光照（direct lighting）：

function rgb radiance(o⃗,d⃗)if ray o⃗+td⃗ hits something thenp⃗=hit pointq⃗=random directionreturn directLightAt(p⃗)+[ρ(q⃗,−d⃗)cos⁡θi/p(q⃗)]∗radiance(p⃗,q⃗)elsereturn background(o⃗,d⃗)\begin{aligned} &\text{function}\ \text{rgb radiance}(\vec{o}, \vec{d}) \\ &\quad\begin{aligned} &\textbf{if}\ \text{ray}\ \vec{o}+t\vec{d}\ \text{hits something}\ \textbf{then} \\ &\quad\begin{aligned} &\vec{p} = \text{hit point} \\ &\vec{q} = \text{random direction} \\ &\textbf{return}\ \text{directLightAt}(\vec{p}) + [\rho(\vec{q}, -\vec{d})\cos\theta_{i}/p(\vec{q})] * \text{radiance}(\vec{p}, \vec{q}) \end{aligned} \\ &\textbf{else} \\ &\quad\textbf{return}\ \text{background}(\vec{o}, \vec{d}) \end{aligned} \end{aligned}

directLightAt(p⃗)\text{directLightAt}(\vec{p}) 用于计算直接光照（direct lighting），即光子从光源出发，不经任何中间物体，直接打到 p⃗\vec{p} 点上。对于完全光滑的材质，BRDF 是一个 δ\delta 函数，因而上述代码无法精确计算，需要引入分支来做特殊处理。

上述代码中，光源自身需要特殊处理。

avatar
文章
阅读
粉丝