前端应该了解的图形学知识(一)
背景
之前写的文章有做 three.js 源码的分享,不熟悉图形学的同学看完会感觉有点晦涩,其中有很多图形学的知识。为了更好了学习这块的内容,查漏补缺,所以在继续解析源码之前,把图形学的刀磨得更锋利些。
这篇文章介绍了坐标系转换的概念和内容,来源参考 3D数学基础:图形与游戏开发这本书,有兴趣的同学可以自己研读一下。
坐标及坐标系
坐标是在特定坐标系下表示物体位置的方法,一谈到坐标,必定是在某个坐标系下给定的。例如经纬度坐标是相对于地球的球面坐标系统给出。而常用的坐标系有笛卡尔坐标系,极坐标系,球面坐标系等。
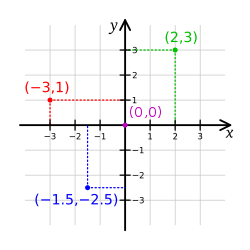
这里拿wiki上的图介绍一下常用的2D笛卡尔坐标系
- 中心点为坐标系原点
- 有两条相互垂直的直线构成坐标系的轴
对于2D笛卡尔坐标系来说,一个点(x,y)的坐标代表点到x,y轴的有符号距离。
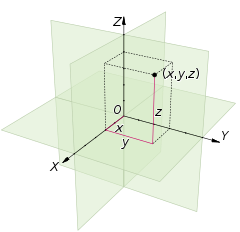
在2D笛卡尔坐标系下添加一个垂直于x、y轴的坐标轴z,且x、y、z轴满足右手定律,那么就构成了一个3D笛卡尔坐标系。
对于3D笛卡尔坐标系来说,一个空间点(x,y,z)的坐标代表点到yz,xz,xy三个面的有符号距离。
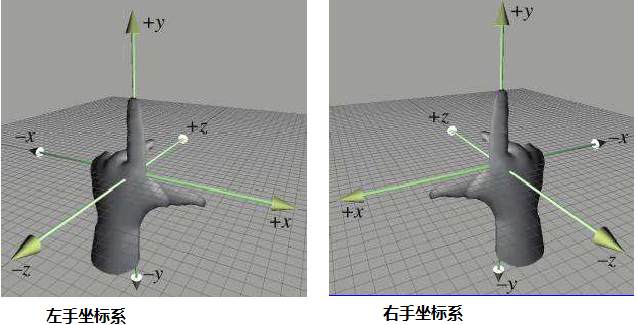
左手坐标系和右手坐标系
当我们旋转一个坐标系之后,就会生成一个新的坐标系。如上一小节内的3d坐标系,绕x轴旋转90度,我们就会得到一个y轴朝下的右手坐标。所以一个简单的结论,这两个坐标系是可以相互旋转得到的。
但不是所有的3D坐标系都一定完全等价,我们将此分为左手坐标系和右手坐标系。
同时以此为旋转的方向也不一样。
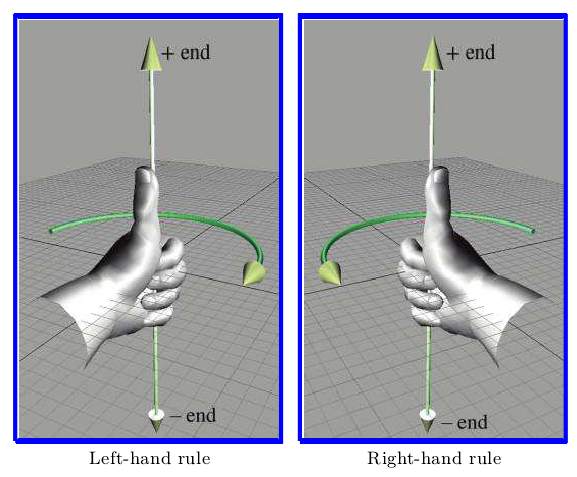
多坐标系的定义
对于任意一个坐标系来说,我们可以宣称它为‘世界’坐标系,因为轴是无线延伸的,所以它可以用坐标表示任意位置的物体。但是当坐标系内的多个物体出现相对偏移时,我们会发现很难在一个坐标系内计算清楚这种偏移。为了方便使用,我们设定了一些有用的坐标系。
世界坐标系
世界坐标系也称作全局坐标系。在当前场景下最大的一个坐标系,它可以用来描述其他所有的坐标系,但不能被更大的、外部的坐标系描述。
物体坐标系
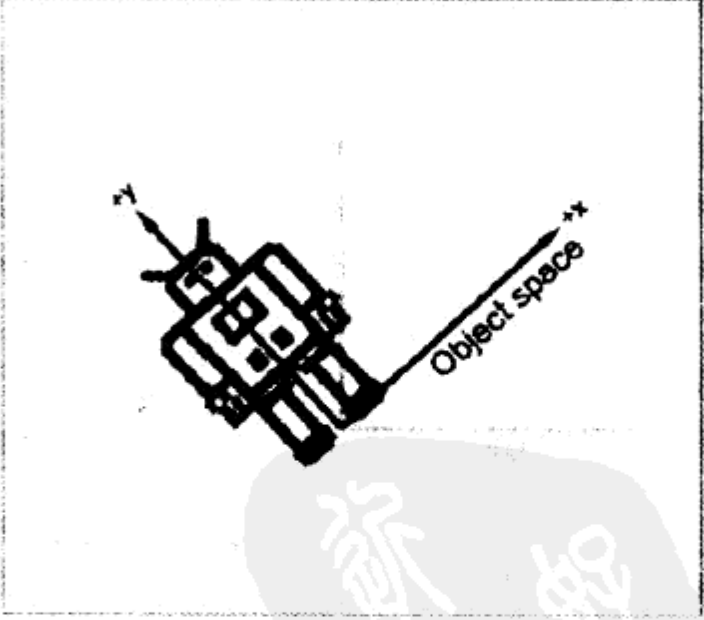
物体坐标系也称作模型坐标系。下图中的机器人构建了一个机器人坐标系。在这个坐标系中,机器人的坐标都是固定的,我们只需要关注机器人具体细节,如眼睛、脚在这个坐标系中的坐标。至于这个机器人在场景中是否和其他物体碰撞,则可以通过坐标系转换,转换到世界坐标系下进行判断。
相机坐标系
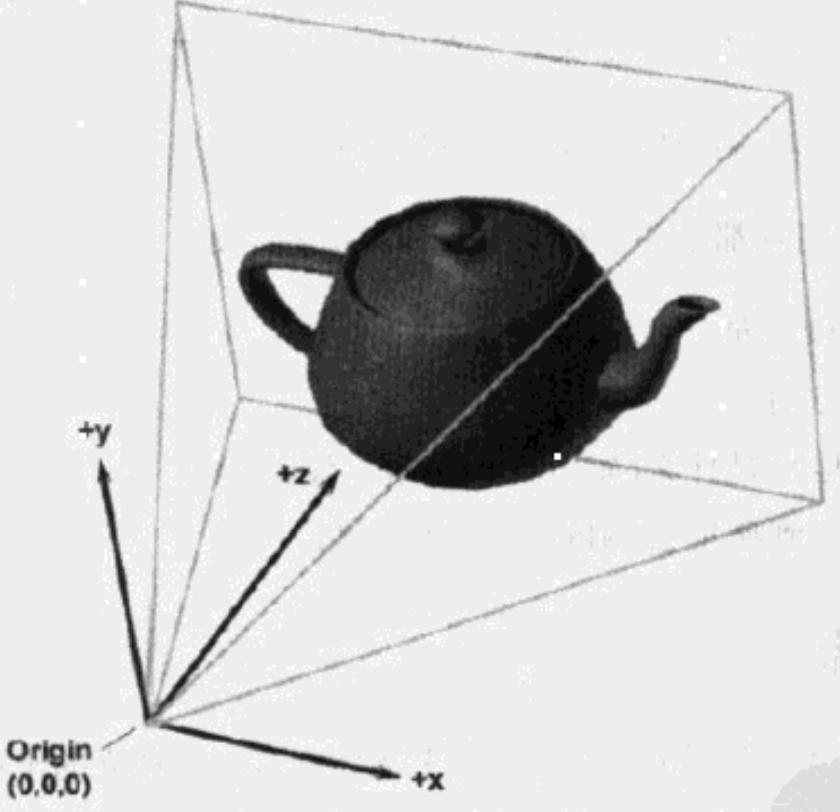
现在我们已经有了一个大的场景(世界坐标系),很多的物体(物体坐标系)。现在我们要给这个场景插入一个相机。物体相机形成的物体坐标系也就是相机坐标系了。相机坐标系代表的是相机视角下的空间坐标,对于真实场景来说,相机成像也是捕获现实中的光影最后映射成照片。那我们其实也就可以在3d空间中,通过相机坐标系、相机参数,我们模拟真实的成像过程,不同于真实场景获取到的照片,这里我们只能收获一些从3d映射到2d的坐标点。
相机坐标会以相机的视角关心以下这些问题
- 世界坐标系的点在相机前方吗?在后方的点不在相机范围内。
- 世界坐标系的点在相机的视椎体范围内吗?在前方的点也要保证在视椎体内,才会被相机捕捉。
- 物体是否是被截断的。相机可能拍不全整个物体。
- 重合物体,谁在前面谁在后面。
坐标系转换
这里拿一个例子解释,在操场上某个位置有一只修狗,在不远处放一些狗狗爱吃的零食。如果狗狗想去吃零食,就会直奔零食而去。
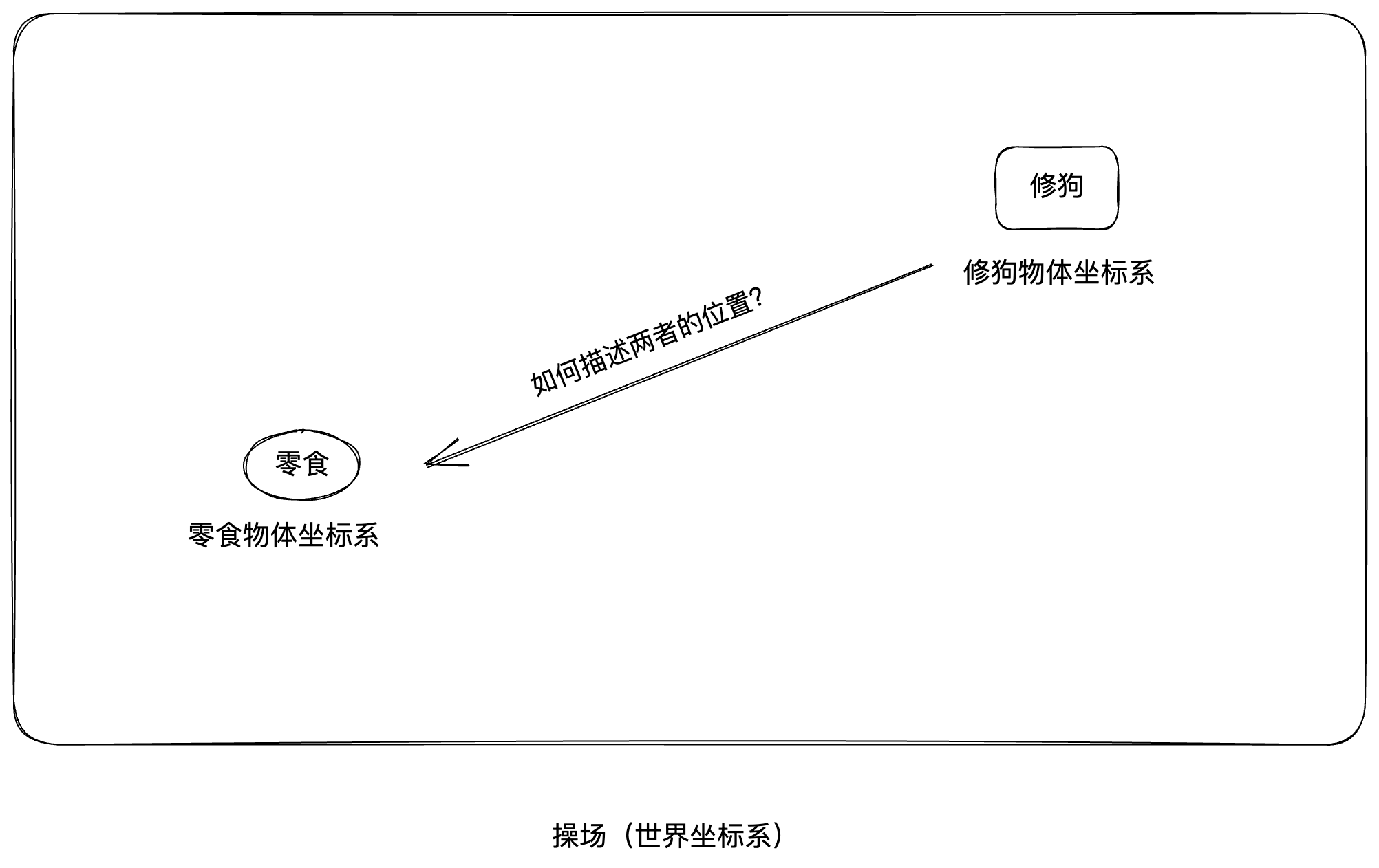
首先我们先考虑这几个对象的静态位置,我们假设零食和狗狗的在操场内是端正的,我们也可以比较容易的定位物体坐标系在操场中的位置。
- 操场为世界坐标系,原点在左下角。
- 零食和修狗在各自的物体的坐标系中,原点在中心。在世界坐标系中,原点坐标分别为(50,50),(200,150)
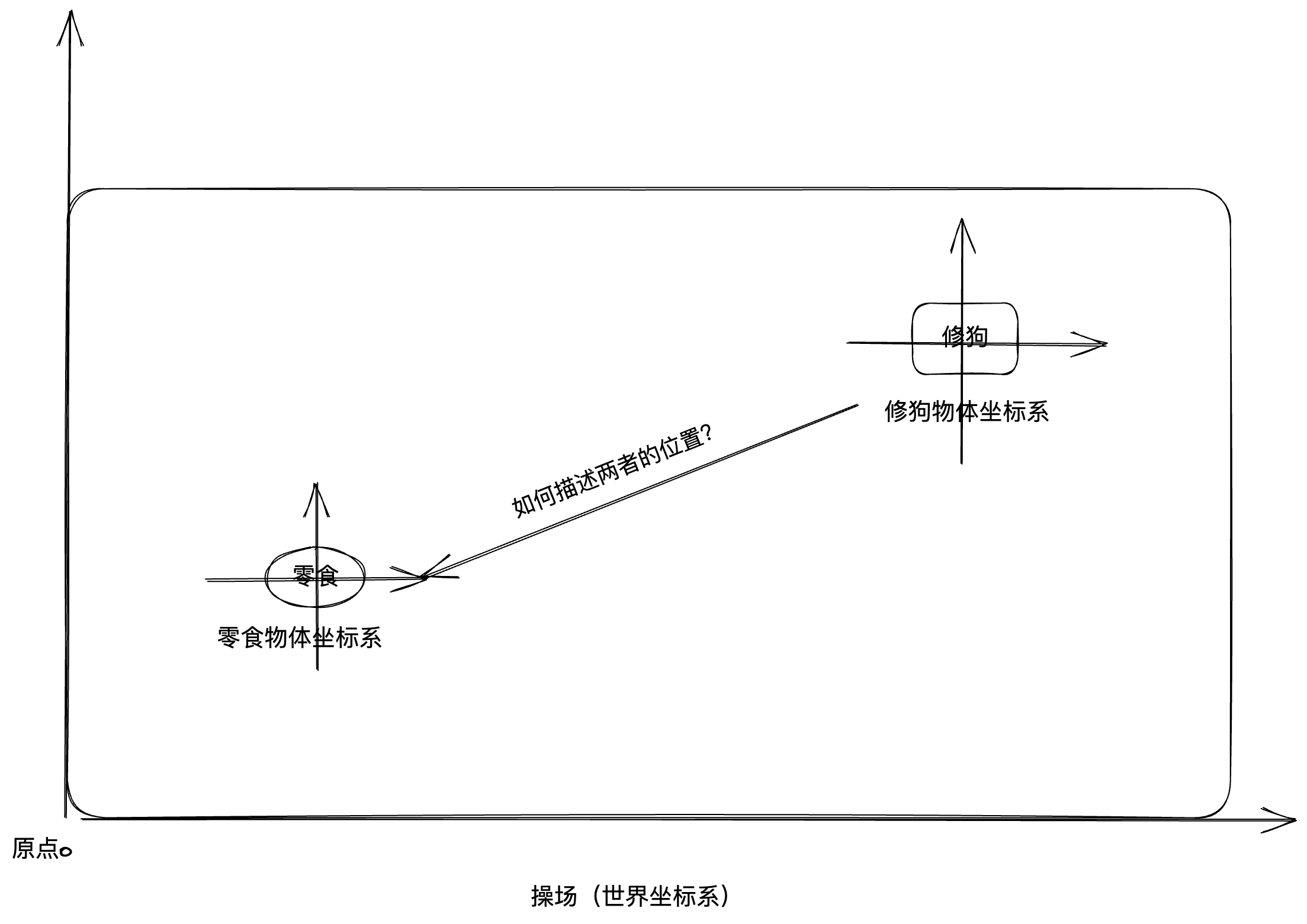
接下来就给修狗开饭了,零食的坐标系下(10,10)位置是修狗最喜欢的罐头。那么如何表示这个修狗离罐头多远,修狗朝哪个方向跑可以吃到罐头呢?
- 将零食物体坐标系向左、向下位移50,50。就和世界坐标系重合了。
- 这样罐头的世界坐标就是(50+10,50+10)
- 修狗和罐头的距离和方向就可以用修狗的世界坐标(200,150)和罐头的世界坐标(60,60)组成的向量表示。
接下来加一些限制条件,因为放零食的人比较马虎,把零食放的歪过去了。
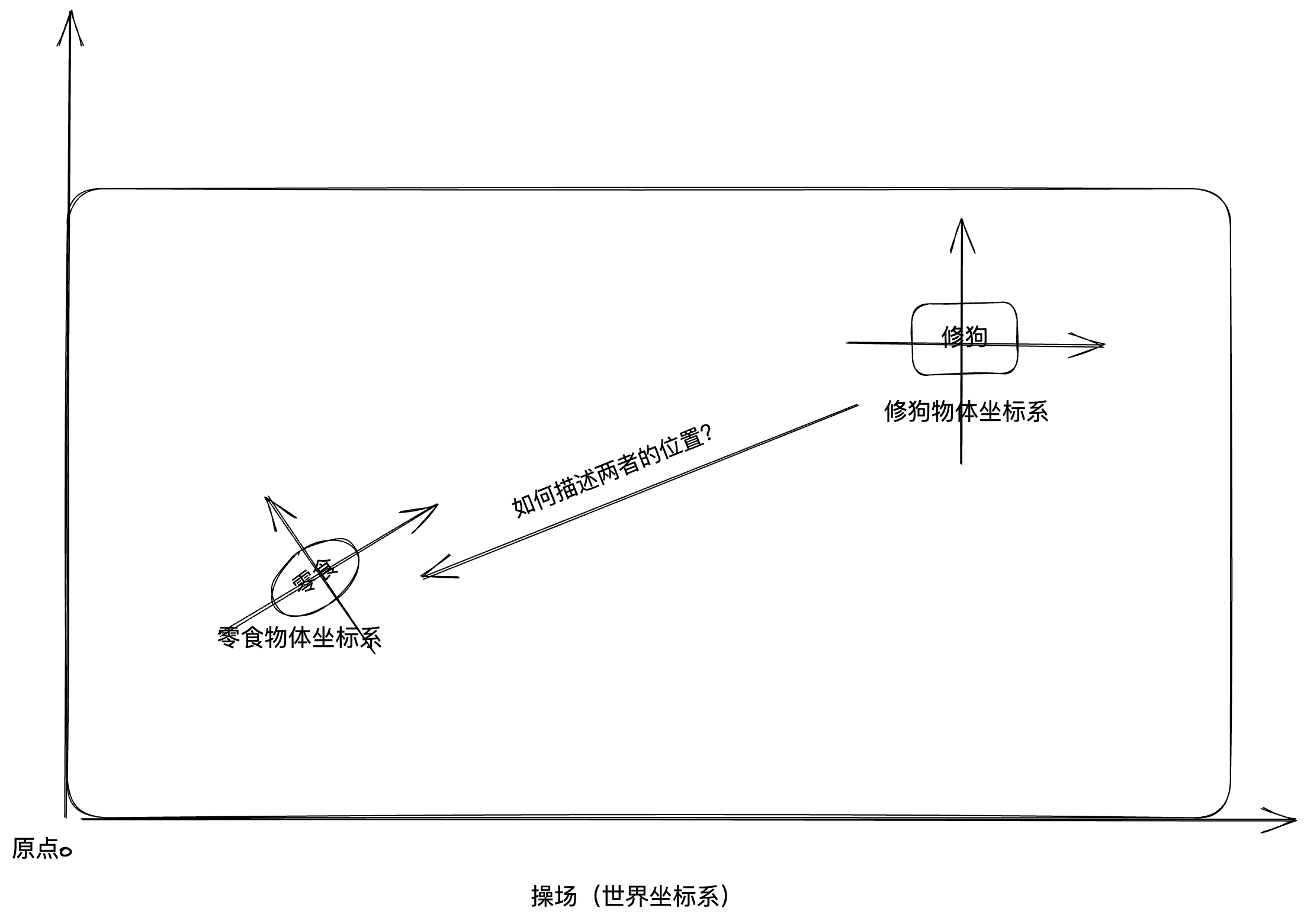
那么我们的修狗想要吃到最喜欢的罐头就需要多做一步了
- 把物体坐标系顺时针旋转45度。那么罐头的坐标就从(10,10)变成了(0,10)
- 将零食物体坐标系向左、向下位移50,50。和世界坐标系重合。罐头的坐标就变成了(50,60)
- 修狗和罐头的距离和方向就可以用修狗的世界坐标(200,150)和罐头的世界坐标(50,60)组成的向量表示。
这是2d里面的坐标系转换,3d的坐标转换也类似。同时只需要通过位移就可以与世界坐标系重合的物体坐标系也被称作惯性坐标系。
现在我们再看上面的修狗例子,如果默认地是平整的,面向屏幕的方向我们再引申出一条坐标轴z轴,所有的坐标都会因此再增加一个新的维度z(因为地是平的,所以坐标z默认都是0)。也是通过旋转、平移得到从物体到世界坐标系的一种转换,唯二的区别就是
- 在z轴上可能会有的旋转分量(零食斜了,修狗斜了)
- 在z轴上的位移分量(零食叠起来了,修狗跳跃!)
这就是一个3D的坐标转换的例子啦。
小结
本文介绍了坐标系和坐标系转换的概念,同时以一个2D操场的例子介绍了如何在一个坐标系中去描述另外一个坐标系。所以大部分的3D模型只需要关注自身的坐标系、旋转、位移,在3D模型被加载到一个场景中时,通过坐标系转换就可以知道模型上的位置在场景中的位置。这种转换关系,在数学中以矩阵的方式表示,在后面的文章我们再一起继续学习这块。