一、概述

高斯网络是一种特殊的概率图模型，它的随机变量的概率分布是连续的高斯分布，而不是普通概率图模型的离散分布。高斯网络可以进一步划分为有向图和无向图两种类型，其中，有向图被称为高斯贝叶斯网络（Gaussian Bayesian Network，GBN），而无向图则被称为高斯马尔可夫网络（Gaussian Markov Network，GMN）。

概率图模型的分类大致如下：

$$P G M\left\{\begin{matrix} \overset{discrete}{\rightarrow}\left\{\begin{matrix} Bayesian\; Network\\ Markov\; Network \end{matrix}\right.\\ \overset{continuous}{\rightarrow}Gaussian\; Network\left\{\begin{matrix} Gaussian\; Bayesian\; Network\\ Gaussian\; Markov\; Network \end{matrix}\right. \end{matrix}\right.$$

高斯网络概率图中的每个节点$x_i$都服从高斯分布，即$x_{i}\sim N(\mu _{i},\Sigma _{i})$，而对于概率图的随机变量$x=\begin{pmatrix} x_{1} & x_{2} & \cdots & x_{p} \end{pmatrix}^{T}$（假设有$p$个节点），也服从参数为$\mu$和$\Sigma$的高斯分布：

$$P(x)=\frac{1}{(2\pi )^{p/2}|\Sigma |^{1/2}}exp\left \{-\frac{1}{2}(x-\mu)^{T}\Sigma ^{-1}(x-\mu)\right \}$$

对于方差矩阵$\Sigma$，定义：

$$\Sigma =[\sigma _{ij}]=\begin{bmatrix} \sigma _{11} & \sigma _{12} & \cdots & \sigma _{1p} \\ \sigma _{21} & \sigma _{22} & \cdots & \sigma _{2p}\\ \vdots & \vdots & \ddots & \vdots \\ \sigma _{p1} & \sigma _{p2} & \cdots & \sigma _{pp} \end{bmatrix}_{p\times p}$$

由方差矩阵我们可以表示全局独立性：

$$x_{i}\perp x_{j}\Leftrightarrow \sigma _{ij}=0$$

对于方差矩阵$\Sigma$的逆，我们定义其为$\Lambda$，叫做精度矩阵（precision matrix）或者信息矩阵（information matrix），即$\Lambda =\Sigma ^{-1}=[\lambda _{ij}]$。通过精度矩阵我们可以表示条件独立性：

$$x_{i}\perp x_{j}|_{x-\left \{x_{i},x_{j}\right \}}\Leftrightarrow \lambda _{ij}=0$$

在本文中只介绍高斯网络有向图和无向图的表示方法，不介绍其他的一些推断的方法。

二、高斯贝叶斯网络

1.有向概率图模型的因子分解

GBN作为一种有向概率图模型，同样服从有向图的因子分解：

$$P(x_{1},x_{2},\cdots ,x_{p})=\prod_{i=1}^{p}P(x_{i}|x_{parent(i)})$$

2.线性高斯模型

GBN从局部来看是一个线性高斯模型，举例来说，就是下面两个两个随机变量之间满足线性关系，同时包含一定的噪声，噪声服从高斯分布：

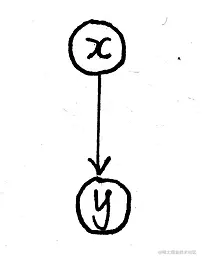
其概率表示如下：

$$P(x)=N(x|\mu _{x},\Sigma _{x})\\ P(y|x)=N(y|Ax+b,\Sigma _{y})$$

3.类比线性动态系统

对于GBN是线性高斯模型这一点可以类比之前讲过的线性动态系统（Linear Dynamic System，LDS），参考链接：卡尔曼滤波

LDS是一种特殊的GBN，它的概率图模型如下：

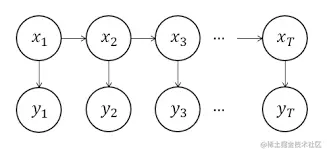
在LDS中每个节点都只有一个父亲节点，其概率为：

$$x_{t}=A\cdot x_{t-1}+B+\varepsilon \\ y_{t}=C\cdot x_{t}+D+\delta \\ \varepsilon \sim N(0,Q)\\ \delta \sim N(0,R)$$

写成条件概率的形式就是：

$$P(z_{t}|z_{t-1})\sim N(A\cdot z_{t-1}+B,Q)\\ P(x_{t}|z_{t})\sim N(C\cdot z_{t}+D,R)\\ z_{1}\sim N(\mu _{1},\Sigma _{1})$$

LDS 的假设是相邻时刻的变量之间的依赖关系，因此是一个局域模型，而GBN每⼀个节点的父亲节点不⼀定只有⼀个，因此可以看成是⼀个全局的模型。

4.高斯贝叶斯网络的表示

在GBN中，对于每一个节点，其概率可以写成以下标准形式：

$$P(x_{i}|x_{parent(i)})=N(x_{i}|\mu _{i}+w_{i}^{T}x_{parent(i)},\sigma _{i}^2)$$

在上面的式子中，将$x_{parent(i)}$当做向量来使用。另外我们也可以将随机变量写成等式的形式：

$$x_{i}=\mu _{i}+\sum _{j\in x_{parent(i)}}w_{ij}(x_{j}-\mu _{j})+\sigma _{i}\varepsilon _{i},\; \; \varepsilon _{i}\sim N(0,1)$$

也就是：

$$x_{i}-\mu _{i}=\sum _{j\in x_{parent(i)}}w_{ij}(x_{j}-\mu _{j})+\sigma _{i}\varepsilon _{i},\; \; \varepsilon _{i}\sim N(0,1)$$

这里将每个随机变量都减去了它的均值，是为了简化模型和计算上的方便。接着定义以下向量和矩阵：

$$\mu =\begin{pmatrix} \mu _{1} & \mu _{2} & \cdots & \mu _{p} \end{pmatrix}^{T}\\ W=[w_{ij}]\\ \varepsilon =\begin{pmatrix} \varepsilon _{1} & \varepsilon _{2} & \cdots & \varepsilon _{p} \end{pmatrix}^{T}\\ S=diag(\sigma _{i})$$

然后将前面的式子写成向量形式：

$$x-\mu =W(x-\mu )+S\varepsilon$$

整理一下，也就有：

$$x-\mu =(I-W)^{-1}S\varepsilon$$

因此协方差矩阵就可以写成：

$$\Sigma =Cov(x)=Cov(x-\mu )$$

三、高斯马尔可夫网络

1.高斯贝叶斯网络的表示

对于无向图的高斯网络，其概率可以表示为：

$$P(x)=\frac{1}{Z}\prod_{i=1}^{p}\underset{node\; potential}{\underbrace{\psi _{i}(x_{i})}}\prod_{i,j\in x}^{p} \underset{edge\; potential}{\underbrace{\psi _{i,j}(x_{i},x_{j})}}$$

而对于多维高斯分布的概率表达形式：

$$P(x)=\frac{1}{(2\pi )^{p/2}|\Sigma |^{1/2}}exp\left \{-\frac{1}{2}(x-\mu)^{T}\Sigma ^{-1}(x-\mu)\right \}$$

我们可以根据上式进行整理来探索上述两个不同的概率公式之间的联系：

$$P(x)\propto exp\left \{-\frac{1}{2}(x-\mu)^{T}\Sigma ^{-1}(x-\mu)\right \}\\ =exp\left \{-\frac{1}{2}(x-\mu)^{T}\Lambda (x-\mu)\right \}\\ =exp\left \{-\frac{1}{2}(x^{T}\Lambda -\mu^{T}\Lambda )(x-\mu )\right \}\\ =exp\left \{-\frac{1}{2}(x^{T}\Lambda x-\underset{标量}{\underbrace{\mu^{T}\Lambda x}}-\underset{标量}{\underbrace{x^{T}\Lambda \mu}}+\mu^{T}\Lambda \mu )\right \}\\ =exp\left \{-\frac{1}{2}(x^{T}\Lambda x-2\mu^{T}\Lambda x+\underset{与x无关}{\underbrace{\mu^{T}\Lambda \mu }})\right \}\\ \propto exp\left \{-\underset{二次}{\underbrace{\frac{1}{2}x^{T}\Lambda x}}+\underset{一次}{\underbrace{(\Lambda \mu )^{T}x}}\right \}$$

经过一番整理我们发现$P(x)$所正比于的函数中包含一个二次项和一个一次项。这里我们将$\Lambda \mu$记作$h$，称为potential vector，即：

$$h=\Lambda \mu =\begin{pmatrix} h_{1}\\ h_{2}\\ \vdots \\ h_{p} \end{pmatrix}$$

从$exp\left \{-\frac{1}{2}x^{T}\Lambda x+(\Lambda \mu )^{T}x\right \}$这个式子中我们可以得到与$x_i$和$x_i,x_j$相关的项，下面的结果通过展开这个式子就可以轻易得到：

$$x_{i}:-\frac{1}{2}x_{i}^{2}\lambda _{ii}+h_{i}x_{i}\\ x_{i},x_{j}:-\frac{1}{2}(\lambda _{ij}x_{i}x_{j}+\lambda _{ji}x_{j}x_{i})=-\lambda _{ij}x_{i}x_{j}$$

这些相关项可以分别对应节点势能和边势能，从而将两个公式联系起来。此外，在一个GMN中，如果两个节点之间没有边，那么它们之间的$\lambda _{ij}$就为0。这表明$x_i,x_j$的相关项构成的势函数只与$\lambda _{ij}$有关，从而可以推导出条件独立性：

$$x_{i}\perp x_{j}|_{x-\left \{x_{i},x_{j}\right \}}\Leftrightarrow \lambda _{ij}=0$$

我们之前的讨论是为了阐明以下观点：一个多维高斯分布对应一个GMN。在学习这个多维高斯分布时，我们不仅可以学习到这个分布的参数，同时也可以学习到这个GMN的结构。这是因为，如果我们学习到$\lambda _{ij}=0$，那么这就意味着在概率图上，对应的两个节点之间没有边。

2.其他性质

对于无向图高斯网络来说，除了满足全局独立性和条件独立性以外，还满足另外一个性质，也就是：

对于任意一个无向图中的节点$x_i$，满足： $x_{i}|_{x-\left \{x_{i}\right \}}\sim N(\sum _{j\neq i}\frac{\lambda _{ij}}{\lambda _{ii}}x_{j},\underset{\sigma _{ii}}{\underbrace{\lambda _{ii}^{-1}}})$ 也就是说$x_i$可以表示为无向图中跟它有连接的$x_{j}$（因为没有连接的$x_{j}$对应的$\lambda _{ij}=0$的线性组合。

上述性质的得出是根据$x=\begin{pmatrix} x_{i}\\ x-\left \{x_{i}\right \} \end{pmatrix}=\begin{pmatrix} x_{a}\\ x_{b} \end{pmatrix}$来求解条件概率分布，而求解高斯分布的条件概率分布的方法在之前的课程中已经介绍过了，参考链接：高斯分布。

“本文正在参加 人工智能创作者扶持计划”