高斯分布

数学期望：μ

方差：σ^2

标准差：σ

随机变量：x

exp：e为底（后续括号内的为幂次）

一、一维情况 MLE

高斯分布在机器学习中占有举足轻重的作用。在 MLE 方法中：

\theta=(\mu,\Sigma)=(\mu,\sigma^{2}),\theta_{MLE}=\mathop{argmax}\limits _{\theta}\log p(X|\theta)\mathop{=}\limits _{iid}\mathop{argmax}\limits _{\theta}\sum\limits _{i=1}^{N}\log p(x_{i}|\theta)

MLE的连等号是因为： $\log P(X \mid \theta)=\log \prod_{i=1}^{N} p\left(x_{i} \mid \theta\right)=\sum_{i=1}^{N} \log p\left(x_{i} \mid \theta\right)$

argmax : 比如f(x)中，x就是变量(arg), arg是argument，即自变量, arg max 意思是使后面式子取到 max值时的变量取值

一般地，高斯分布的概率密度函数PDF（probability density function）写为：

p(x|\mu,\Sigma)=\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}e^{-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu)}

带入 MLE 中我们考虑一维的情况

\log p(X|\theta)=\sum\limits _{i=1}^{N}\log p(x_{i}|\theta)=\sum\limits _{i=1}^{N}\log\frac{1}{\sqrt{2\pi}\sigma}\exp(-(x_{i}-\mu)^{2}/2\sigma^{2})

=\sum_{i=1}^{N}\left[\log \frac{1}{\sqrt{2 x}}+\log \frac{1}{\sigma}-\frac{\left(x_{i}-\mu\right)^{2}}{2 \sigma^{2}}\right]

首先对 $\mu$ 的极值可以得到：（ $\mu$ 相对容易）

\mu_{MLE}=\mathop{argmax}\limits _{\mu}\log p(X|\theta)=\mathop{argmax}\limits _{\mu}\sum\limits _{i=1}^{N}(x_{i}-\mu)^{2}

于是：（其实就是均值，且 $\mu_{MLE} = \mu$ )

\frac{\partial}{\partial\mu}\sum\limits _{i=1}^{N}(x_{i}-\mu)^{2}=0\longrightarrow\mu_{MLE}=\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}

其次对 $\theta$ 中的另一个参数 $\sigma$ ，有：

\begin{aligned} \sigma_{MLE}=\mathop{argmax}\limits _{\sigma}\log p(X|\theta)&=\mathop{argmax}\limits _{\sigma}\sum\limits _{i=1}^{N}[-\log\sigma-\frac{1}{2\sigma^{2}}(x_{i}-\mu)^{2}]\\ &=\mathop{argmin}\limits _{\sigma}\sum\limits _{i=1}^{N}[\log\sigma+\frac{1}{2\sigma^{2}}(x_{i}-\mu)^{2}] \end{aligned}

于是：

\frac{\partial}{\partial\sigma}\sum\limits _{i=1}^{N}[\log\sigma+\frac{1}{2\sigma^{2}}(x_{i}-\mu)^{2}]=0\longrightarrow\sigma_{MLE}^{2}=\frac{1}{N}\sum\limits _{i=1}^{N}(x_{i}-\mu)^{2}

值得注意的是，上面的推导中，首先对 $\mu$ 求 MLE，然后利用这个结果求 $\sigma_{MLE}$ ，因此可以预期的是对数据集求期望时 $\mathbb{E}_{\mathcal{D}}[\mu_{MLE}]$ 是无偏差的：

\mathbb{E}_{\mathcal{D}}[\mu_{MLE}]=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}]=\frac{1}{N}\sum\limits _{i=1}^{N}\mathbb{E}_{\mathcal{D}}[x_{i}]=\mu

但是当对 $\sigma_{MLE}$ 求期望的时候由于使用了单个数据集的 $\mu_{MLE}$ ，因此对所有数据集求期望的时候我们会发现 $\sigma_{MLE}$ 是有偏的：

有偏的原因是因为用样本均值 $\mu_{MLE}$ 代替总体均值，假如本身系统设计时均值是已知的。只用MLE算方差的话，除以n也还是无偏估计

另外、如果 $E[\hat{\mu}] = \mu$ 那么，像这种样子我们就认为他是无偏的，如果 ≠ 则是无偏的

补充：下述公式中倒数第二行变化，是因为离散型随机变量方差计算公式：(只要未知数套上了一层E，默认就是常数处理了。)
$D(X)=E\left((X-E(X))^{2}\right)=E\left(X^{2}\right)-E^{2}(X)$

\begin{aligned} \mathbb{E}_{\mathcal{D}}[\sigma_{MLE}^{2}]&=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}(x_{i}-\mu_{MLE})^{2}]=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}(x_{i}^{2}-2x_{i}\mu_{MLE}+\mu_{MLE}^{2}) \\&=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}^{2}-\mu_{MLE}^{2}]=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}^{2}-\mu^{2}-(\mu_{MLE}^{2}-\mu^{2})]\\ &= \mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}^{2}-\mu^{2}]-\mathbb{E}_{\mathcal{D}}[\mu_{MLE}^{2}-\mu^{2}]\\ &=\frac{1}{N} \sum_{i=1}^{N}({\mathbb{E}_{\mathcal{D}}\left(x_{i}^{2}\right)-\mu^{2}})-(\mathbb{E}_{\mathcal{D}}[\mu_{MLE}^{2}]-\mathbb{E}_{\mathcal{D}}^{2}[\mu_{MLE}])\\&= \sigma^{2}-(\mathbb{E}_{\mathcal{D}}[\mu_{MLE}^{2}]-\mu^{2})=\sigma^{2}-(\mathbb{E}_{\mathcal{D}}[\mu_{MLE}^{2}]-\mathbb{E}_{\mathcal{D}}^{2}[\mu_{MLE}])=\sigma^{2}-Var[\mu_{MLE}]\\&=\sigma^{2}-Var[\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}]=\sigma^{2}-\frac{1}{N^{2}}\sum\limits _{i=1}^{N}Var[x_{i}]=\frac{N-1}{N}\sigma^{2} \end{aligned}

可以理解为当 $\mu$ 取 $\mu_{M L E}$ 就已经确定了所有 $x_{i}$ 的和等于 $N \mu_{M L E}$ ，也就是说当 N-1 个 $x_{i}$ 确定以后，第 N 个 $x_{i}$ 也就被确定了，所以少了一个"自由度"，因此 $E\left[\sigma_{M L E}^{2}\right]=\frac{N-1}{N} \sigma^{2}$

所以真正的 $\sigma^2$ 为：

\hat{\sigma}^{2}=\frac{1}{N-1}\sum\limits _{i=1}^{N}(x_{i}-\mu_{MLE})^{2}

得到结论：求得有偏的方差，将样本总数减一即为无偏的方差（有偏的方差 < 无偏的方差）方差往小的方向估计了，也就是用极大似然估计确实会带来一定的偏差，对于高斯分布来说就是估计小了

也很好理解，因为样本是总体的一部分，而方差是所有样本的分布情况，随着样本的增加，方差会增大

此外，在抽样时，样本落在中间区域的概率大，所以抽样的数据离散程度小于总体，所以抽样方差小，也很好理解

二、多维情况

多维高斯分布表达式为：

\begin{array}{c} x \stackrel{i i d}{\sim} N(\mu, \Sigma)=p(x|\mu,\Sigma)=\frac{1}{(2 \pi)^{D / 2}|\Sigma|^{1 / 2}} \exp (-\frac{1}{2} \underbrace{(x-\mu)^{T} \Sigma^{-1}(x-\mu)}_{\text {二次型 }}) \\ x \in \mathbb{R}^{p}, r \cdot v \\ x=\left(\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{p} \end{array}\right) \mu=\left(\begin{array}{c} \mu_{1} \\ \mu_{2} \\ \vdots \\ \mu_{p} \end{array}\right) \Sigma=\left[\begin{array}{cccc} \sigma_{11} & \sigma_{12} & \cdots & \sigma_{1 p} \\ \sigma_{21} & \sigma_{22} & \cdots & \sigma_{2 p} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{p 1} & \sigma_{p 2} & \cdots & \sigma_{p p} \end{array}\right]_{p \times p} \end{array}

$\Sigma$ 一般是半正定的, 在本次证明中假设是正定的, 即所有的特征值都是正的，没有 0 。

其中 $x,\mu\in\mathbb{R}^{p},\Sigma\in\mathbb{R}^{p\times p}$ ， $\Sigma$ 为协方差矩阵，一般而言也是半正定矩阵。这里我们只考虑正定矩阵。对于我们高维的高斯分布，未知数只有自变量 $x$ ，其余的 $\mu$ 、 $\Sigma$ 都可以当做常量处理。首先我们处理指数上的数字，指数上的数字可以记为 $x$ 和 $\mu$ 之间的马氏距离。

马氏距离

$\sqrt{(x-\mu)^{T}\Sigma ^{-1}(x-\mu)}为马氏距离（x与\mu之间，当\Sigma为I时马氏距离即为欧氏距离。$

正定矩阵与半正定矩阵

给定一个大小为 $n \times n$ 的实对称矩阵 $A$ ，若对于任意长度为 $n$ 的非零向量 $\boldsymbol{x}$ ，有 $\boldsymbol{x}^{T} A \boldsymbol{x}>0$ 恒成立，则矩阵 $A$ 是一个正定矩阵，有 $\boldsymbol{x}^{T} A \boldsymbol{x} \geq 0$ 恒成立，则矩阵 $A$ 是一个半正定矩阵。

三、证明高斯分布等高线为"椭圆"

协方差矩阵的特征值分解

任意的 $N \times N$ 实对称矩阵都有 $N$ 个线性无关的特征向量。并且这些特征向量都可以正交单位化而得到一组正交且模为 1 的向量。故实对称矩阵 $\Sigma$ 可被分解成 $\Sigma=U\Lambda U^{T}$ 。

\begin{gathered} & \text { 将 } \Sigma \text { 进行特征分解, } \Sigma=U \Lambda U^T \\ & \text { 其中 } U U^T=U^T U=I, \quad \underset{i=1,2, \cdots, p}{=\operatorname{diag}}\left(\lambda_i\right), U=\left(u_1, u_2, \cdots, u_p\right)_{p \times p} \\ & \text { 因此 } \Sigma=U \Lambda U^T \\ & =\left(\begin{array}{llll} u_1 & u_2 & \cdots & u_p \end{array}\right)\left[\begin{array}{cccc} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_p \end{array}\right]\left(\begin{array}{c} u_1^T \\ u_2^T \\ \vdots \\ u_p^T \end{array}\right) \\ & =\left(\begin{array}{llll} u_1 \lambda_1 & u_2 \lambda_2 & \cdots & u_p \lambda_p \end{array}\right)\left(\begin{array}{c} u_1^T \\ u_2^T \\ \vdots \\ u_p^T \end{array}\right) \\ & =\sum_{i=1}^p u_i \lambda_i u_i^T \\ & \Sigma^{-1}=\left(U \Lambda U^T\right)^{-1}=\left(U^T\right)^{-1} \Lambda^{-1} U^{-1}=U \Lambda^{-1} U^T=\sum_{i=1}^p u_i \frac{1}{\lambda_i} u_i^T \\ &\text {, 其中 } \Lambda^{-1}=\operatorname{diag}\left(\frac{1}{\lambda_i}\right), i=1,2, \cdots, p \\ & \end{gathered}

将概率密度整理成椭圆方程的形式

\begin{array}{l} \Delta=(x-\mu)^{T} \Sigma^{-1}(x-\mu) \\ =(x-\mu)^{T} \sum_{i=1}^{p} u_{i} \frac{1}{\lambda_{i}} u_{i}^{T}(x-\mu) \\ =\sum_{i=1}^{p}(x-\mu)^{T} u_{i} \frac{1}{\lambda_{i}} u_{i}^{T}(x-\mu) \\ \left(\text { 令 } y_{i}=(x-\mu)^{T} u_{i}\right) \\ =\sum_{i=1}^{p} y_{i} \frac{1}{\lambda_{i}} y_{i}^{T} \\ =\sum_{i=1}^{p} \frac{y_{i}^{2}}{\lambda_{i}} \\ \end{array}

上式中 $y_{i}=(x-\mu )^{T}u _{i}$ 可以理解为将 $x$ 减去均值进行中心化以后再投影到 $u _{i}$ ( $u_{i}$ 是正交矩阵的一个基向量，代表一个坐标轴)方向上，相当于做了一次坐标轴变换。 $y_{i}$ 是 $x-\mu$ 在特征向量 $u_{i}$ 上的投影长度，因此上式子就是 $\Delta$ 取不同值时的同心椭圆。

当 $x$ 的维度为2即 $p=2$ 时 $\Delta =\frac{y_{1}^{2}}{\lambda _{1}}+\frac{y_{2}^{2}}{\lambda _{2}}$ ，得到类似椭圆方程的等式，所以也就可以解释为什么其等高线是椭圆形状。二维高斯分布的图像如下所示：

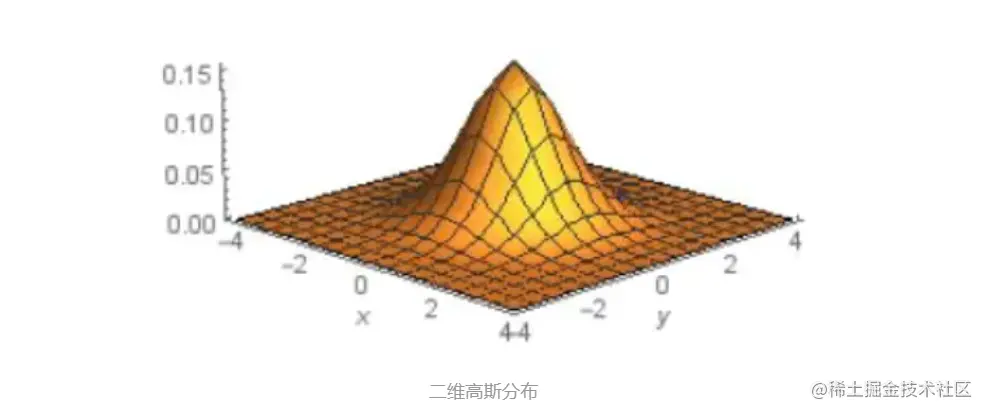
所以随着 $x$ 的取值不断变化，即在维度为2的情况下，椭圆的长轴和短轴的长度也随着唯一自变量 $x$ 不断改变，切面也就不断变大和变小。

四、高斯分布的局限性

参数过多协方差矩阵 $\Sigma_{p \times p}$ 中的参数共有 $1+2+\cdots+p=\frac{p(p+1)}{2}$ 个 ( $\Sigma_{p \times p}$ 是对称矩阵(参数个数少一半左右))），因此当 $x$ 的维度 $p$ 很大时，高斯分布的参数就会有很多，其计算复杂度为 $O\left(p^{2}\right)$ ) 。可以通过假设高斯分布的协方差矩阵为对角矩阵来减少参数，当高斯分布的协方差矩阵为对角矩阵(仅对角线上有参数)时，无需特征值分解，特征向量的方向就会和原坐标轴的方向平行，因此高斯分布的等高线 (同心椭圆) 就不会倾斜。另外如果在高斯分布的协方差矩阵为对角矩阵为对角矩阵的基础上使得其特征值全部相等 (即 $\lambda_{1}=\lambda_{2}=\cdots=\lambda_{i}$ ）, 则高斯分布的等高线就会成为一个圆形，而且不会倾斜，称为各向同性。

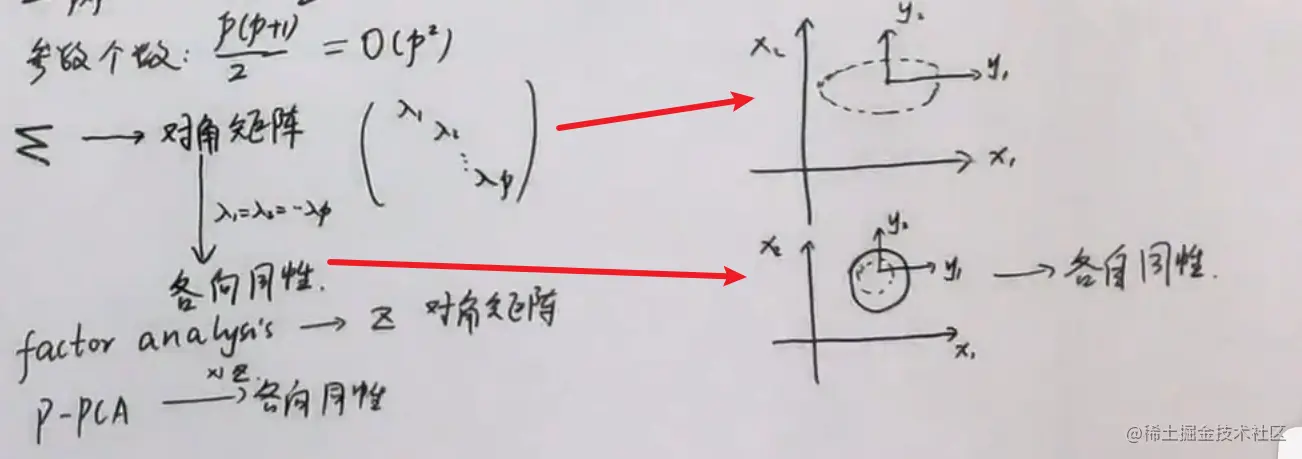
$\Sigma$ 若退化为对角矩阵，那么 $\left(y_{i}=(x-\mu)^{T} x_{i}\right)$ ，即每一个样本x代表它本身，U已经不存在（SVD分解，将U代表旋转，^代表特征值），方向与若 $x_{i}$ 保持方正（而每一个 $x_{i}$ 独立同分布）。 ^ 中的 $\lambda_{i}$ 均相等，则持有特向同性，退化为圆

单个高斯分布是单峰，对有多个峰的数据分布不能得到好的结果，拟合能力有限解决方案是使用多个高斯分布，比如高斯混合GMM模型。

五、求高斯分布的边缘概率与条件概率

概述

首先将变量、均值和方差进行划分：

$x=\left(\begin{array}{l}x_a \\ x_b\end{array}\right), 其中 x_a 是 m 维的, x_b 是 n 维的。$ $\mu=\left(\begin{array}{c} \mu_a \\ \mu_b \end{array}\right) \Sigma=\left(\begin{array}{cc} \Sigma_{a a} & \Sigma_{a b} \\ \Sigma_{b a} & \Sigma_{b b} \end{array}\right)$

本部分旨在根据上述已知来求 $P\left(x_a\right), P\left(x_b \mid x_a\right), P\left(x_b\right), P\left(x_a \mid x_b\right)$ 。 2. 定理以下定义为推导过程中主要用到的定理，这里只展示定理的内容，不进行证明:

$已知 x \sim N(\mu, \Sigma), x \in \mathbb{R}^p\\ y=A x+B, y \in \mathbb{R}^q\\ 结论: y \sim N\left(A \mu+B, A \Sigma A^T\right)$

一个简单但不严谨的证明:

$\begin{gathered} E[y]=E[A x+B]=A E[x]+B=A \mu+B \\ \operatorname{Var}[y]=\operatorname{Var}[A x+B] \\ =\operatorname{Var}[A x]+\operatorname{Var}[B] \\ =A \operatorname{Var}[x] A^T+0 \\ =A \Sigma A^T \end{gathered}$

求边缘概率 $P\left(x_a\right)$

$\begin{gathered} x_a=\underbrace{\left(\begin{array}{ll} I_m & 0_n \end{array}\right)}_A \underbrace{\left(\begin{array}{c} x_a \\ x_b \end{array}\right)}_x \\ E\left[x_a\right]=\left(\begin{array}{ll} I_m & 0_n \end{array}\right)\left(\begin{array}{c} \mu_a \\ \mu_b \end{array}\right)=\mu_a \\ \operatorname{Var}\left[x_a\right]=\left(\begin{array}{ll} I_m & 0_n \end{array}\right)\left(\begin{array}{cc} \Sigma_{a a} & \Sigma_{a b} \\ \Sigma_{b a} & \Sigma_{b b} \end{array}\right)\left(\begin{array}{c} I_m \\ 0_n \end{array}\right) \\ =\left(\begin{array}{ll} \Sigma_{a a} & \Sigma_{a b} \end{array}\right)\left(\begin{array}{c} I_m \\ 0_n \end{array}\right)=\Sigma_{a a} \end{gathered}$

所以 $x_a \sim N\left(\mu_a, \Sigma_{a a}\right)$ ，同理 $x_b \sim N\left(\mu_b, \Sigma_{b b}\right)$ 。 4. 求条件概率 $P\left(x_b \mid x_a\right)$

$\begin{gathered} & \text { 构造 }\left\{\begin{array}{c} x_{b \cdot a}=x_b-\Sigma_{b a} \Sigma_{a a}^{-1} x_a \\ \mu_{b \cdot a}=\mu_b-\Sigma_{b a} \Sigma_{a a}^{-1} \mu_a \\ \Sigma_{b b \cdot a}=\Sigma_{b b}-\Sigma_{b a} \Sigma_{a a}^{-1} \Sigma_{a b} \end{array}\right. \\ & \text { ( } \Sigma_{b b \cdot a} \text { 是 } \Sigma_{a a} \text { 的舒尔补) } \\ & x_{b \cdot a}=\underbrace{\left(\begin{array}{ll} \Sigma_{b a} \Sigma_{a a}^{-1} & I_n \end{array}\right)}_A \underbrace{\left(\begin{array}{c} x_a \\ x_b \end{array}\right)}_x \\ & E\left[x_{b \cdot a}\right]=\left(\begin{array}{cc} -\Sigma_{b a} \Sigma_{a a}^{-1} & I_n \end{array}\right)\left(\begin{array}{l} \mu_a \\ \mu_b \end{array}\right)=\mu_b-\Sigma_{b a} \Sigma_{a a}^{-1} \mu_a=\mu_{b \cdot a} \\ & \operatorname{Var}\left[x_{b \cdot a}\right]=\left(\begin{array}{cc} -\Sigma_{b a} \Sigma_{a a}^{-1} & I_n \end{array}\right)\left(\begin{array}{cc} \Sigma_{a a} & \Sigma_{a b} \\ \Sigma_{b a} & \Sigma_{b b} \end{array}\right)\left(\begin{array}{c} -\Sigma_{a a}^{-1} \Sigma_{b a}^T \\ I_n \end{array}\right) \\ & =\left(\begin{array}{cc} -\Sigma_{b a} \Sigma_{a a}^{-1} \Sigma_{a a}+\Sigma_{b a} & -\Sigma_{b a} \Sigma_{a a}^{-1} \Sigma_{a b}+\Sigma_{b b} \end{array}\right) \\ & =\left(\begin{array}{ll} 0 & -\Sigma_{b a} \Sigma_{a a}^{-1} \Sigma_{a b}+\Sigma_{b b} \end{array}\right)\left(\begin{array}{c} -\Sigma_{a a}^{-1} \Sigma_{b a}^T \\ I_n \end{array}\right) \\ & =\Sigma_{b b}-\Sigma_{b a} \Sigma_{a a}^{-1} \Sigma_{a b} \\ & =\Sigma_{b b \cdot a} \\ & \end{gathered}$

现在可以得到 $x_{b \cdot a} \sim N\left(\mu_{b \cdot a}, \Sigma_{b b \cdot a}\right)$ 。根据 $x_b$ 与 $x_{b \cdot a}$ 的关系可以得到 $x_b \mid x_a$ 的分布:

$x_b=\underbrace{x_{b \cdot a}}_x+\underbrace{\Sigma_{b a} \Sigma_{a a}^{-1} x_a}_B\\ (在求条件概率 P\left(x_b \mid x_a\right) 时 x_a 对于 x_b 来说可以看做已知, 因此上式中 \Sigma_{b a} \Sigma_{a a}^{-1} x_a 看做常量 B )\\ \begin{gathered} E\left[x_b \mid x_a\right]=\mu_{b \cdot a}+\Sigma_{b a} \Sigma_{a a}^{-1} x_a \\ \operatorname{Var}\left[x_b \mid x_a\right]=\operatorname{Var}\left[x_{b \cdot a}\right]=\Sigma_{b b \cdot a} \end{gathered}\\$

因此可以得到 $x_b \mid x_a \sim N\left(\mu_{b \cdot a}+\Sigma_{b a} \Sigma_{a a}^{-1} x_a, \Sigma_{b b \cdot a}\right)$ , 同理可以得到 $x_a \mid x_b \sim N\left(\mu_{a \cdot b}+\Sigma_{a b} \Sigma_{b b}^{-1} x_b, \Sigma_{a a \cdot b}\right)$ 。

六、求高斯分布的联合概率分布

概述

$\begin{gathered} p(x)=N\left(x \mid \mu, \Lambda^{-1}\right) \\ p(y \mid x)=N\left(y \mid A x+b, L^{-1}\right)\\ \Lambda 和 L 是精度矩阵 (precision matrix), precision matrix =(\text { covariance matrix })^T 。\\ \end{gathered}$

本部分旨在根据上述已知来求 $p(y), p(x \mid y)$ 。

求解 $p(y)$

由上述已知可以确定 $y$ 与 $x$ 的关系为线性高斯模型， $\varepsilon$ 是人为定义的噪声，分布也是人为设定。

则 $y$ 与 $x$ 符合下述关系:

y=A x+b+\varepsilon, \varepsilon \sim N\left(0, L^{-1}\right)

然后求解 $y$ 的均值和方差:

\begin{gathered} E[y]=E[A x+b+\varepsilon]=E[A x+b]+E[\varepsilon]=A \mu+b \\ \operatorname{Var}[y]=\operatorname{Var}[A x+b+\varepsilon]=\operatorname{Var}[A x+b]+\operatorname{Var}[\varepsilon]=A \Lambda^{-1} A^T+L^{-1} \end{gathered}

则可以得出 $y \sim N\left(A \mu+b, L^{-1}+A \Lambda^{-1} A^T\right)$

求解 $p(x \mid y)$

求解 $p(x \mid y)$ 需要首先求解 $x$ 与 $y$ 的联合分布，然后根据上一部分的公式直接得到 $p(x \mid y)$ 。

$构造 z=\left(\begin{array}{l}x \\ y\end{array}\right) \sim N\left(\left[\begin{array}{c}\mu \\ A \mu+b\end{array}\right],\left[\begin{array}{cc}\Lambda^{-1} & \Delta \\ \Delta^T & L^{-1}+A \Lambda^{-1} A^T\end{array}\right]\right)\\ 现在需要求解 \Delta\\ \begin{gathered} \Delta=\operatorname{Cov}(x, y) \\ =E\left[(x-E[x])(y-E[y])^T\right] \\ =E\left[(x-\mu)(y-A \mu-b)^T\right] \\ =E\left[(x-\mu)(A x+b+\varepsilon-A \mu-b)^T\right] \\ =E\left[(x-\mu)(A x-A \mu+\varepsilon)^T\right] \\ =E\left[(x-\mu)(A x-A \mu)^T+(x-\mu) \varepsilon^T\right] \\ =E\left[(x-\mu)(A x-A \mu)^T\right]+E\left[(x-\mu) \varepsilon^T\right]\\ (因为 x \perp \varepsilon, 所以 (x-\mu) \perp \varepsilon, 所以 E\left[(x-\mu) \varepsilon^T\right]=E[(x-\mu)] E\left[\varepsilon^T\right] )\\ =E\left[(x-\mu)(A x-A \mu)^T\right]+E[(x-\mu)] E\left[\varepsilon^T\right] \\ =E\left[(x-\mu)(A x-A \mu)^T\right]+E[(x-\mu)] \cdot 0 \\ =E\left[(x-\mu)(A x-A \mu)^T\right] \\ =E\left[(x-\mu)(x-\mu)^T A^T\right] \\ =E\left[(x-\mu)(x-\mu)^T\right] A^T \\ =\operatorname{Var}[x] A^T \\ =\Lambda^{-1} A^T\\ 由此可得 z=\left(\begin{array}{l}x \\ y\end{array}\right) \sim N\left(\left[\begin{array}{c}\mu \\ A \mu+b\end{array}\right],\left[\begin{array}{cc}\Lambda^{-1} & \Lambda^{-1} A^T \\ A \Lambda^{-1} & L^{-1}+A \Lambda^{-1} A^T\end{array}\right]\right)\\ 套用上一部分的公式可以得到 x \mid y \sim N\left(\mu_{x \cdot y}+\Lambda^{-1} A^T\left(L^{-1}+A \Lambda^{-1} A^T\right)^{-1} y, \Sigma_{x x \cdot y}\right) \end{gathered}$

『白板推导系列笔记』2.高斯分布