流形上的预积分，用于实时的视觉惯性里程计On-Manifold Preintegration for Real-Time

On-Manifold Preintegration for Real-Time Visual-Inertial Odometry

讲预积分的资料很多，但是总有很多我觉得不顺畅和难以理解的地方，因此直接选择看原论文，获取第一手的资料是个不错的选择。

这篇论文的公式推导简直是蔚为大观，惊为天人，不敢想象工作量有多大，对状态估计的理解有多深。

因子图中的因子，即factor等同于residual。

这篇文章的前导部分太多了，因此直接从第V部分看起。

V. IMU Model and Motion Integration

IMU测量模型：

\begin{aligned} { }_{\mathrm{B}} \tilde{\boldsymbol{\omega}}_{\mathrm{WB}}(t) &={ }_{\mathrm{B}} \boldsymbol{\omega}_{\mathrm{WB}}(t)+\mathbf{b}^{g}(t)+\boldsymbol{\eta}^{g}(t) \\ { }_{\mathrm{B}} \tilde{\mathbf{a}}(t) &=\mathrm{R}_{\mathrm{WB}}^{\top}(t)\left({ }_{\mathrm{w}} \mathbf{a}(t)-{ }_{\mathrm{w}} \mathbf{g}\right)+\mathbf{b}^{a}(t)+\boldsymbol{\eta}^{a}(t), \end{aligned}

IMU测得的量是角速度 ${ }_{\mathrm{B}} \tilde{\boldsymbol{\omega}}_{\mathrm{WB}}(t)$ 和线加速度 ${ }_{\mathrm{B}} \tilde{\mathbf{a}}(t)$ 。这两个测量值都包含了加性高斯白噪声 $\boldsymbol{\eta^g(t)},\boldsymbol{b}^a(t)$ 和缓慢变化传感器偏差 $\boldsymbol{b}^g(t),\boldsymbol{b}^a(t)$ ，这里的偏差服从随机游走分布。简单理解成每次测量都有偏差，但是偏差都会有些许不同，因此偏差也是待估计的量。除此之外，角速度是直接放置在IMU坐标系下的，但是线加速度真值需要先减去重力加速度，先放置在世界坐标系下，之后再用旋转矩阵变换到IMU坐标系下。

微小时间内积分获得旋转矩阵、线速度、平移量：

\begin{array}{l} \mathrm{R}_{\mathrm{WB}}(t+\Delta t)=\mathrm{R}_{\mathrm{WB}}(t) \operatorname{Exp}\left(\int_{t}^{t+\Delta t}{ }_{\mathrm{B}} \boldsymbol{\omega}_{\mathrm{wB}}(\tau) d \tau\right) \\ _\mathrm{w} \mathbf{v}(t+\Delta t)={ }_{\mathrm{w}} \mathbf{v}(t)+\int_{t}^{t+\Delta t}{ }_{\mathrm{w}} \mathbf{a}(\tau) d \tau \\ _\mathrm{w}\mathbf{p}(t+\Delta t)={ }_{\mathrm{w}} \mathbf{p}(t)+\int_{t}^{t+\Delta t} {}_{\mathrm{w}} \mathbf{v}(\tau) d \tau+\iint_{t}^{t+\Delta t} {}_{\mathrm{w}}{\mathbf{a}}(\tau) d \tau^{2} . \end{array}

这里的 $\mathrm{Exp}()$ 是 $\mathrm{exp}(\cdot^{\wedge})$ 的简写方式。公式（1）把角速度在时间上积分就能获得旋转向量，也就是李代数 $\phi$ ，之后再指数映射为旋转矩阵。公式（2）（3）容易理解，不要需要注意是在世界坐标系下的。

假设短时间内匀速运动，离散化积分公式：

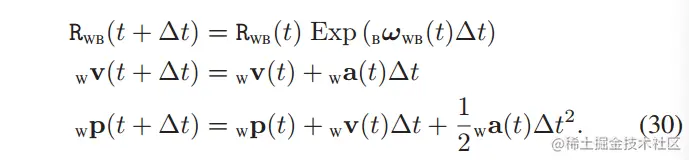
代入IMU模型：

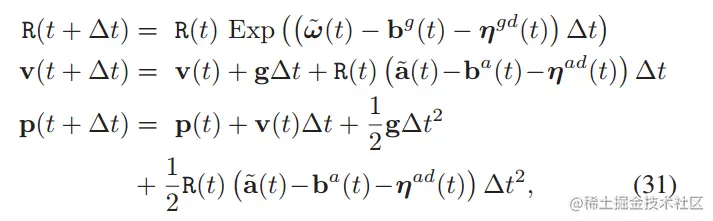
离散后的高斯分布协方差：

\operatorname{Cov}\left(\boldsymbol{\eta}^{g d}(t)\right)=\frac{1}{\Delta t} \operatorname{Cov}\left(\boldsymbol{\eta}^{g}(t)\right)

VI. IMU Preintergeration on Manifold

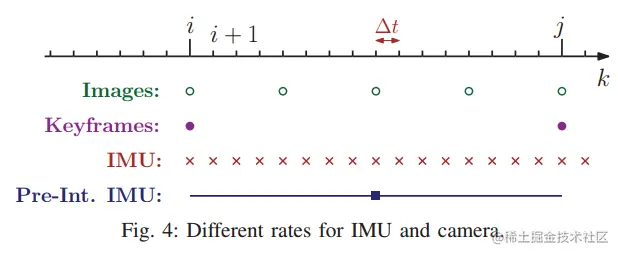对关键帧 $i$ 和 $j$ 之间的所有测量值进行积分获得 $j$ 时的状态：

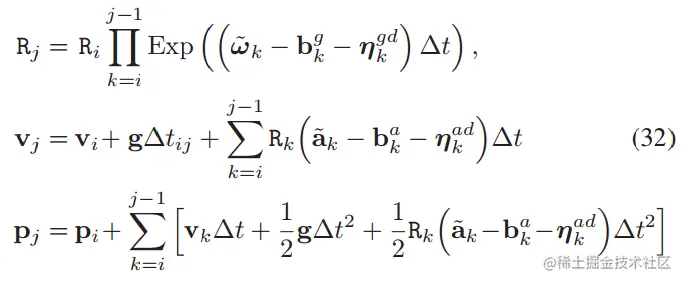
直接积分的坏处/采用预积分的原因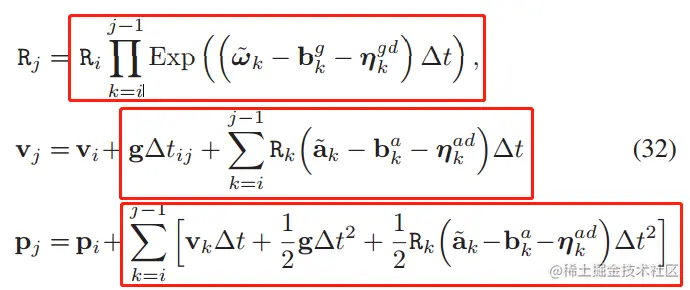： 1649647468(1).png 上述的公式中，为了方便，我们先不把偏差看成变量，而是已知常量，那么我们容易根据这三个公式构建出三种误差项，并且把上图中红色部分看成观测值。因为IMU的频率比较高，计算积分是很花时间的，因此这部分红色框中的"观测值"，我们希望它是常量的，不用每次迭代优化都得重新计算一次，就像重投影误差中的特征点坐标一样。

但是事与愿违，由于第23个公式中都包含了 $R_k$ ，而 $R_k$ 的计算方法与 $R_j$ 相似，都是得最前面乘上一个 $R_i$ ，那么一旦 $R_i$ 在迭代优化中更新了，那么 $R_k$ 也需要跟着更新，第23个公式中的积分就得重新再算。这一点原论文是这样阐述的：

将积分项与 $\boldsymbol{Ri}$ 解耦，构建新的测量模型

因此最好是把积分中的 $R_k$ 左乘上 $R_i$ 的转置（就是逆），那么我们可以定义相对运动增量（relative motion increments），从而使得积分项脱离与 $R_i$ 的耦合关系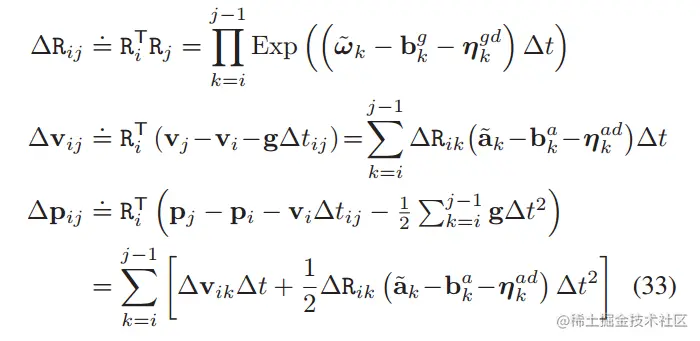：而这其中除了 $\Delta R_{i,j}$ 有明确的物理含义，即 $i$ , $j$ 之间的相对旋转矩阵外，其它两项实际上并没有明显的物理含义，只是为了解耦 $R_i$ 而拼凑出来的。

但是有一点很遗憾，上面我们假设了偏差 $\boldsymbol{b}$ 是常量，但是实际上它也是优化量，但是上面的过程并没有把它从积分项中解放出来。下面的VI-A我们仍然假设它是常量，VI-C中会对它的估计进行讨论，文章其他部分，我们则假设两关键帧之间偏差不变，即：

\mathbf{b}_{i}^{g}=\mathbf{b}_{i+1}^{g}=\ldots=\mathbf{b}_{j-1}^{g}, \quad \mathbf{b}_{i}^{a}=\mathbf{b}_{i+1}^{a}=\ldots=\mathbf{b}_{j-1}^{a}

A. Preintegrated IMU Measurements

前置公式：

\operatorname{Exp}(\phi+\delta \boldsymbol{\phi}) \approx \operatorname{Exp}(\boldsymbol{\phi}) \operatorname{Exp}\left(\mathrm{J}_{r}(\boldsymbol{\phi}) \delta \boldsymbol{\phi}\right) \\ \operatorname{Exp}(\phi) \mathrm{R}=\mathrm{R} \operatorname{Exp}\left(\mathrm{R}^{\top} \phi\right)

由于上面的公式中的高斯噪声被封印在积分项中，这导致上面的公式很难被直接代入MAP中，因此我们希望能够把噪声从积分项中分离出来。

分离噪声 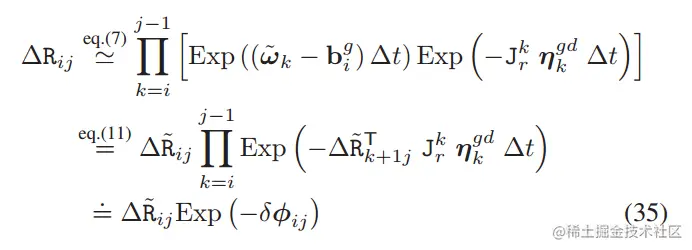这公式在代入前置公式(2)时似乎存在顺序问题，但是暂且不管。其中， $\mathrm{J}_{r}^{k} \doteq \mathrm{J}_{r}^{k}\left(\left(\tilde{\boldsymbol{\omega}}_{k}-\mathbf{b}_{i}^{g}\right) \Delta t\right)$ ，预积分旋转测量值 $\Delta \tilde{\mathrm{R}}_{i j} \doteq\prod_{k=i}^{j-1} \operatorname{Exp}\left(\left(\tilde{\boldsymbol{\omega}}_{k}-\mathbf{b}_{i}^{g}\right) \Delta t\right)$ ，对应的噪声为 $\delta \phi_{i,j}$ 。

旋转矩阵若服从高斯分布，写法如下：

\tilde{\mathrm{R}}=\mathrm{R} \operatorname{Exp}(\epsilon), \quad \epsilon \sim \mathcal{N}(0, \Sigma)

虽然这里的噪声是指数映射之后再乘上去，但是如果用BCH公式进行进行的话，就可以拆分成李代数上的加法。从而与一般的观测公式统一起来，即 $观测值=f(优化变量)+观测噪声$ ，对应到这里就是 $f(优化变量)=观测值-观测噪声$ 。

速度也采用类似的方法对噪声进行分离：其中， $\Delta \tilde{\mathbf{v}}_{i j} \doteq \sum_{k=i}^{j-1} \Delta \tilde{\mathrm{R}}_{i k}\left(\tilde{\mathbf{a}}_{k}-\mathbf{b}_{i}^{a}\right) \Delta t$ ，噪声为 $\delta \mathbf{v}_{i j}$ ，可以看到这个形式也是符合我们上面说的观测公式的形式。

对于平移向量也是如此

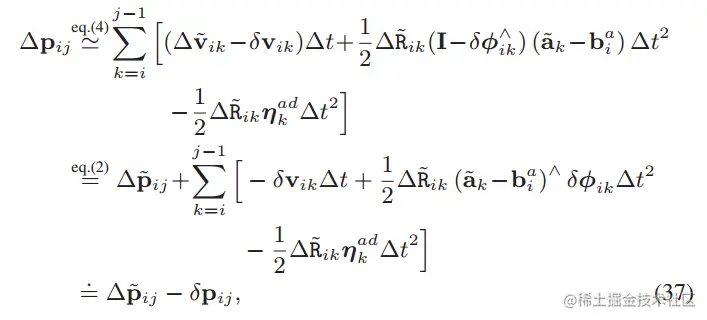
构建观测公式形式

把优化变量带进去，调整一下形式，就变成真正的观测公式了。

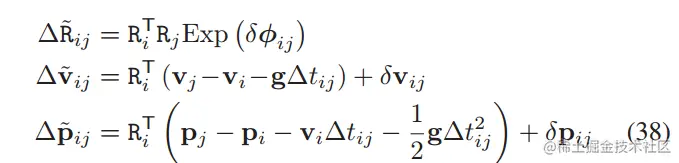
B. Noise Propagation

A中虽然构建了观测公式，并且获得了三种噪声 $\left[\delta \phi_{i j}^{\top}, \delta \mathbf{v}_{i j}^{\top}, \delta \mathbf{p}_{i j}^{\top}\right]^{\top}$ ，这三种噪声服从的是均值为0的高斯分布，但是协方差我们并不知道。实际上，我们只知道最初观测时的高斯噪声的协方差，但是这里的噪声经过了层层计算，因此协方差需要重新推导。【这里涉及到《机器人的状态估计》中高斯分布的变换】

也是说我们希望知道下式中的 $\Sigma_{i,j}$

\boldsymbol{\eta}_{i j}^{\Delta} \doteq\left[\delta \boldsymbol{\phi}_{i j}^{\top}, \delta \mathbf{v}_{i j}^{\top}, \delta \mathbf{p}_{i j}^{\top}\right]^{\top} \sim \mathcal{N}\left(\mathbf{0}_{9 \times 1}, \boldsymbol{\Sigma}_{i j}\right)

高斯噪声的协方差传播

这是从前面的推导中以及知道旋转噪声的形式：

\operatorname{Exp}\left(-\delta \boldsymbol{\phi}_{i j}\right) \doteq \prod_{k=i}^{j-1} \operatorname{Exp}\left(-\Delta \tilde{\mathrm{R}}_{k+1 j}^{\top} \mathrm{J}_{r}^{k} \boldsymbol{\eta}_{k}^{g d} \Delta t\right)

两边取对数：

\delta \boldsymbol{\phi}_{i j}=-\log \left(\prod_{k=i}^{j-1} \operatorname{Exp}\left(-\Delta \tilde{\mathrm{R}}_{k+1 j}^{\top} \mathrm{J}_{r}^{k} \boldsymbol{\eta}_{k}^{g d} \Delta t\right)\right)

注意这里取对数之后，并不能直接对数抵消指数，然后把李代数相加，而是需要用BCH公式进行进行，但是由于噪声实际上很小，所以近似时的雅克比近似于单位矩阵，因此最后才得到的是李代数相加，即：

\delta \boldsymbol{\phi}_{i j} \simeq \sum_{k=i}^{j-1} \Delta \tilde{\mathrm{R}}_{k+1 j}^{\top} \mathrm{J}_{r}^{k} \boldsymbol{\eta}_{k}^{g d} \Delta t

速度和平移量噪声的形式为：

\begin{array}{l} \delta \mathbf{v}_{i j} \simeq \sum_{k=i}^{j-1}\left[-\Delta \tilde{\mathrm{R}}_{i k}\left(\tilde{\mathbf{a}}_{k}-\mathbf{b}_{i}^{a}\right)^{\wedge} \delta \boldsymbol{\phi}_{i k} \Delta t+\Delta \tilde{\mathrm{R}}_{i k} \boldsymbol{\eta}_{k}^{a d} \Delta t\right] \\ \delta \mathbf{p}_{i j} \simeq \sum_{k=i}^{j-1}\left[\delta \mathbf{v}_{i k} \Delta t-\frac{1}{2} \Delta \tilde{\mathrm{R}}_{i k}\left(\tilde{\mathbf{a}}_{k}-\mathbf{b}_{i}^{a}\right)^{\wedge} \delta \boldsymbol{\phi}_{i k} \Delta t^{2}+\frac{1}{2} \Delta \tilde{\mathrm{R}}_{i k} \boldsymbol{\eta}_{k}^{a d} \Delta t^{2}\right] \end{array}

从上面的推导可以看出，三种噪声 $\boldsymbol{\eta}_{i j}^{\Delta} =\left[\delta \phi_{i j}^{\top}, \delta \mathbf{v}_{i j}^{\top}, \delta \mathbf{p}_{i j}^{\top}\right]^{\top}$ 都是原观测噪声 $\boldsymbol{\eta}_{k}^{d} \doteq\left[\boldsymbol{\eta}_{k}^{g d}, \boldsymbol{\eta}_{k}^{a d}\right]$ 的线性函数，既然是高斯分布的线性变换，那么传播后的协方差 $\Sigma_{i,j}$ 就比较容易求解了。

为了实时运行，实际上，我们对 $\Sigma_{i,j}$ 是采用不断迭代更新的方式进行计算的，即当一个新的IMU测量值到达时，就更新 $\Sigma_{i,j}$ 。

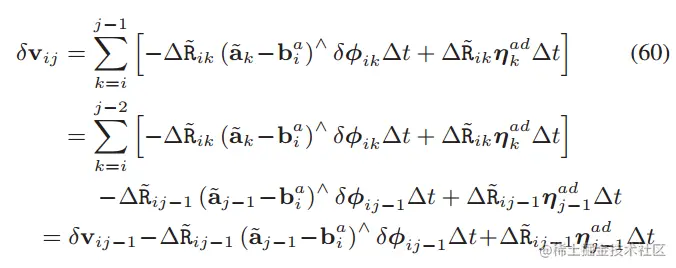
下面我们先推导高斯噪声的迭代形式：（大概看看就行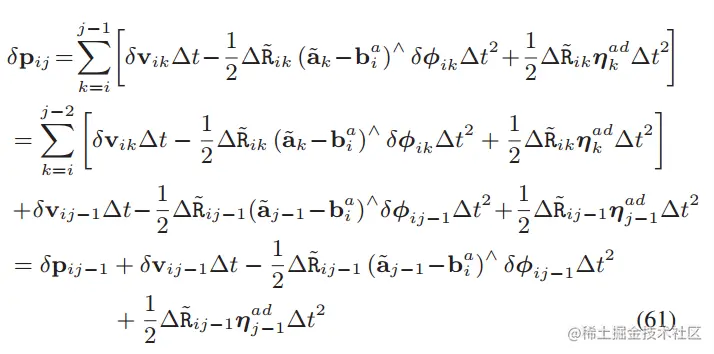）把上面三个迭代公式写成紧凑的矩阵：

\boldsymbol{\eta}_{i j}^{\Delta}=\mathbf{A}_{j-1} \boldsymbol{\eta}_{i j-1}^{\Delta}+\mathbf{B}_{j-1} \boldsymbol{\eta}_{j-1}^{d}

现在形式很明朗了，上述对高斯分布的迭代更新是线性的，因此很容易得到迭代后的协方差的计算公式：

\boldsymbol{\Sigma}_{i j}=\mathbf{A}_{j-1} \boldsymbol{\Sigma}_{i j-1} \mathbf{A}_{j-1}^{\top}+\mathbf{B}_{j-1} \boldsymbol{\Sigma}_{\boldsymbol{\eta}} \mathbf{B}_{j-1}^{\top}

迭代从 $\boldsymbol{\Sigma}_{i i}=\mathbf{0}_{9 \times 9}$ 。

到这里可以阶段性总结一下预积分的步骤：在i和j的时间段内，随着新的角速度和线加速度测量值不断送过来，我们可以累加更新三种观测值，同时更新对应的协方差，直到该时间段内的测量值都被包含进去，我们就获得了三个观测方程。

C. Incorporation Bias Updates

上述讨论中，偏差 $b= \left \{b_i^a,b_i^g \right \}$ 被视为常量，但实际上它也是待估计的量。如果 $b$ 进行更新，即 $\mathbf{b} \leftarrow \overline{\mathbf{b}}+\delta \mathbf{b}$ ，由于积分项中包含了 $b$ ，那么就得重新进行积分了，很麻烦。因此最好是得到一种迭代更新形式，类似上面的协方差，那么我们可以进行一阶展开：

\begin{aligned} \Delta \tilde{\mathrm{R}}_{i j}\left(\mathbf{b}_{i}^{g}\right) & \simeq \Delta \tilde{\mathrm{R}}_{i j}\left(\overline{\mathbf{b}}_{i}^{g}\right) \operatorname{Exp}\left(\frac{\partial \Delta \overline{\mathbf{R}}_{i j}}{\partial \mathbf{b}^{g}} \delta \mathbf{b}^{g}\right) \\ \Delta \tilde{\mathbf{v}}_{i j}\left(\mathbf{b}_{i}^{g}, \mathbf{b}_{i}^{a}\right) & \simeq \Delta \tilde{\mathbf{v}}_{i j}\left(\overline{\mathbf{b}}_{i}^{g}, \overline{\mathbf{b}}_{i}^{a}\right)+\frac{\partial \Delta \overline{\mathbf{v}}_{i j}}{\partial \mathbf{b}^{g}} \delta \mathbf{b}_{i}^{g}+\frac{\partial \Delta \overline{\mathbf{v}}_{i j}}{\partial \mathbf{b}^{a}} \delta \mathbf{b}_{i}^{a} \\ \Delta \tilde{\mathbf{p}}_{i j}\left(\mathbf{b}_{i}^{g}, \mathbf{b}_{i}^{a}\right) & \simeq \Delta \tilde{\mathbf{p}}_{i j}\left(\overline{\mathbf{b}}_{i}^{g}, \overline{\mathbf{b}}_{i}^{a}\right)+\frac{\partial \Delta \overline{\mathbf{p}}_{i j}}{\partial \mathbf{b}^{g}} \delta \mathbf{b}_{i}^{g}+\frac{\partial \Delta \overline{\mathbf{p}}_{i j}}{\partial \mathbf{b}^{a}} \delta \mathbf{b}_{i}^{a} \end{aligned}

即，新的观测值=旧的观测值+旧的观测值对 $b$ 的梯度* $b$ 的增量。

接下来需要对则其中五个雅克比的形式进行推导。以旋转矩阵为例(基本上是各种近似，大概看看就行)：

新的观测值为：

\Delta \tilde{\mathbf{R}}_{i j}\left(\hat{\mathbf{b}}_{i}\right)=\prod_{k=i}^{j-1} \operatorname{Exp}\left(\left(\tilde{\boldsymbol{\omega}}_{k}-\hat{\mathbf{b}}_{i}^{g}\right) \Delta t\right)

把 $\mathbf{b} \leftarrow \overline{\mathbf{b}}+\delta \mathbf{b}$ 代进去，可以得到：

\begin{aligned} \Delta \tilde{\mathbf{R}}_{i j}\left(\hat{\mathbf{b}}_{i}\right) &=\prod_{k=i}^{j-1} \operatorname{Exp}\left(\left(\tilde{\boldsymbol{\omega}}_{k}-\left(\overline{\mathbf{b}}_{i}^{g}+\delta \mathbf{b}_{i}^{g}\right)\right) \Delta t\right) \\ & \simeq \prod_{k=i}^{j-1} \operatorname{Exp}\left(\left(\tilde{\boldsymbol{\omega}}_{k}-\overline{\mathbf{b}}_{i}^{g}\right) \Delta t\right) \operatorname{Exp}\left(-\mathrm{J}_{r}^{k} \delta \mathbf{b}_{i}^{g} \Delta t\right) \end{aligned}

\Delta \tilde{\mathrm{R}}_{i j}\left(\hat{\mathbf{b}}_{i}\right)=\Delta \overline{\mathrm{R}}_{i j} \prod_{k=i}^{j-1} \operatorname{Exp}\left(-\Delta \tilde{\mathrm{R}}_{k+1 j}\left(\overline{\mathbf{b}}_{i}\right)^{\top} \mathrm{J}_{r}^{k} \delta \mathbf{b}_{i}^{g} \Delta t\right)

\begin{aligned} \Delta \tilde{\mathrm{R}}_{i j}\left(\hat{\mathbf{b}}_{i}\right) & \simeq \Delta \overline{\mathrm{R}}_{i j} \operatorname{Exp}\left(\sum_{k=i}^{j-1}-\Delta \tilde{\mathrm{R}}_{k+1 j}\left(\overline{\mathbf{b}}_{i}\right)^{\top} \mathrm{J}_{r}^{k} \delta \mathbf{b}_{i}^{g} \Delta t\right) \\ &=\Delta \overline{\mathrm{R}}_{i j} \operatorname{Exp}\left(\frac{\partial \Delta \overline{\mathrm{R}}_{i j}}{\partial \mathbf{b}^{g}} \delta \mathbf{b}_{i}^{g}\right) \end{aligned}

这样就求出了其中一个雅克比，其他的类似，最后有：

\begin{aligned} \frac{\partial \Delta \overline{\mathrm{R}}_{i j}}{\partial \mathbf{b}^{g}} &=-\sum_{k=i}^{j-1}\left[\Delta \tilde{\mathbf{R}}_{k+1 j}\left(\overline{\mathbf{b}}_{i}\right)^{\top} \mathrm{J}_{r}^{k} \Delta t\right] \\ \frac{\partial \Delta \mathbf{v}_{i j}}{\partial \mathbf{b}^{a}} &=-\sum_{k=1}^{j-1} \Delta \overline{\mathrm{R}}_{i k} \Delta t \\ \frac{\partial \Delta \mathbf{\overline { b }}_{i j}}{\partial \mathbf{b}^{g}} &=-\sum_{k=i}^{j-1} \Delta \overline{\mathrm{R}}_{i k}\left(\tilde{\mathbf{a}}_{k}-\overline{\mathbf{b}}_{i}^{a}\right)^{\wedge} \frac{\partial \Delta \overline{\mathrm{R}}_{i k}}{\partial \mathbf{b}^{g}} \Delta t \\ \frac{\partial \Delta \overline{\mathbf{b}}_{i j}}{\partial \mathbf{b}^{a}} &=\sum_{k=i}^{j-1} \frac{\partial \Delta \overline{\mathbf{v}}_{i k}}{\partial \mathbf{b}^{a}} \Delta t-\frac{1}{2} \Delta \overline{\mathrm{R}}_{i k} \Delta t^{2} \\ \frac{\partial \Delta \overline{\mathbf{p}}_{i j}}{\partial \mathbf{b}^{g}} &=\sum_{k=i}^{j-1} \frac{\partial \Delta \overline{\mathbf{v}}_{i k}}{\partial \mathbf{b}^{g}} \Delta t-\frac{1}{2} \Delta \overline{\mathrm{R}}_{i k}\left(\tilde{\mathbf{a}}_{k}-\overline{\mathbf{b}}_{i}^{a}\right)^{\wedge} \frac{\partial \Delta \overline{\mathrm{R}}_{i k}}{\partial \mathbf{b}^{g}} \Delta t^{2} \end{aligned}

值得注意的是，这里的雅克比可以通过加上新的项进行更新。

D. Preintegraed IMU Factors

下面给出三种残差定义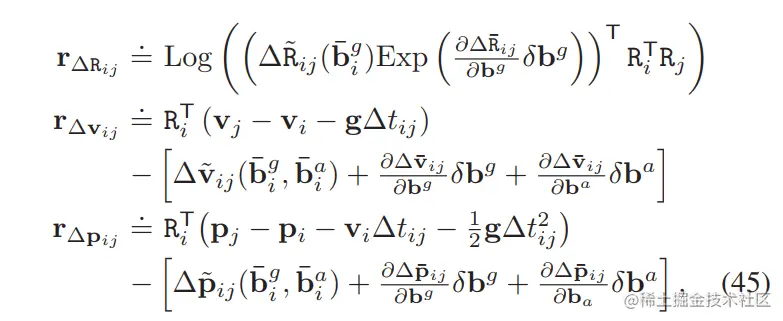：可以看出，其中的积分项是对偏差 $b$ 的一阶展开，并且旋转残差最后转化为李代数，用李代数向量的模来衡量误差大小，也是常用的方法。

上面的误差共9维，而优化变量维度为15维，即

总结一下，论文首先给出了IMU的测量模型，其中的关键是线加速度的测量包含了旋转矩阵；然后对测量模型进行积分，给出了旋转矩阵、速度、平移的定义，并对积分进行离散化；由于积分项中包含了 $R_i$ ，为了避免优化变量更新后需要重新积分，于是将 $R_i$ 从中解耦，并初步整理形成观测模型公式；由于噪声包含了积分项中，不利于放入MAP，于是把噪声从中分离出来，于是观测模型公式完成；由于新的噪声是原始噪声的高斯变换，因此推导出新的噪声的协方差迭代更新公式；由于偏差也是优化变量，因此对观测量对偏差进行一阶展开，从而将偏差变量从中分离。

运行，从第i帧开始，每来一个新的观测值，都累加到三种观测值中，并对协方差矩阵进行更新。