前缀和、差分思想

一维数组

原理

• —维数组A
• 前缀和数组S

$S[i]=\displaystyle\sum_{i=1}^nA[i]=S[i-1]+A[i]$

• 子段和——A中第l个数到第r个数的和

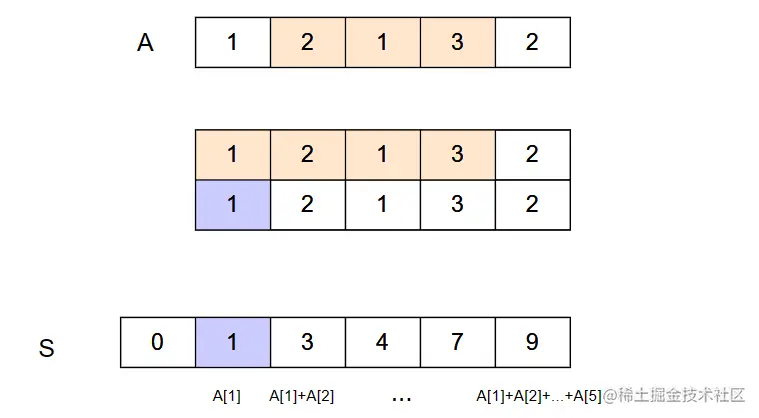
$sum(l,r)=\displaystyle\sum_{i=1}^rA[i]=S[r]-S[l-1]$

• 当A中都是非负数时，前缀和数组S单调递增

时间复杂度

操作	时间复杂度	备注
计算前n项和	O(n)
第l个数到第r个数的和	O(r-l+1)	最坏时间复杂度O(n)

二维数组

原理

• 二维数组A
• 前缀和数组S

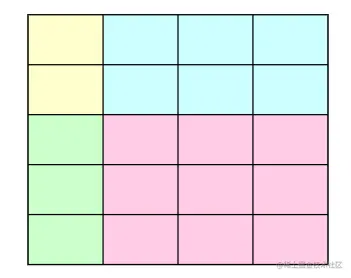
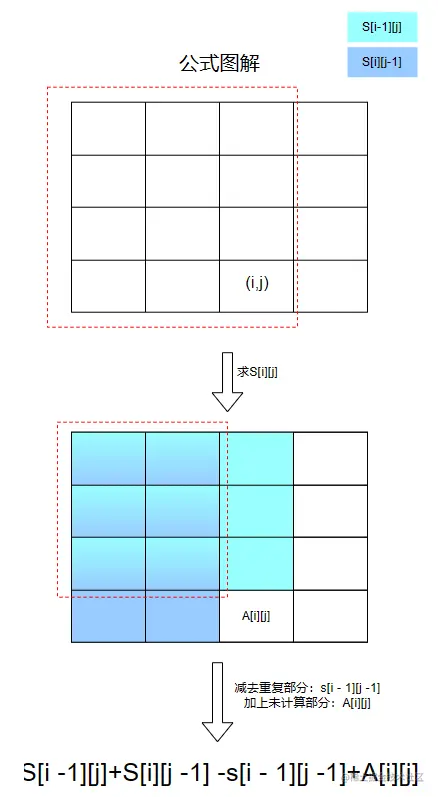
$S[i][j]=\displaystyle\sum_{x=1}^i\displaystyle\sum_{y=1}^jA[x][y]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+A[i][j]$

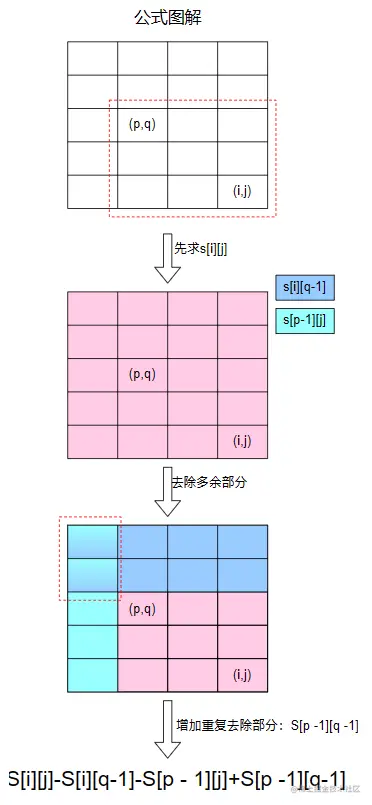
• 子矩阵和---一（p,q）为左上角，（i,j）为右上角的A子矩阵中数的和

$sum(p,q,i,j)=\displaystyle\sum_{x=p}^i\displaystyle\sum_{y=q}^jA[x][y]=S[i][j]-S[i][q-1]-S[p-1][j]+S[p-1][q-1]$

时间复杂度

二维前缀和的时间复杂度其实可以类比一维的时间复杂度，就是把这个二维数组遍历一遍，这样的话就是O(n*m) 的时间复杂度

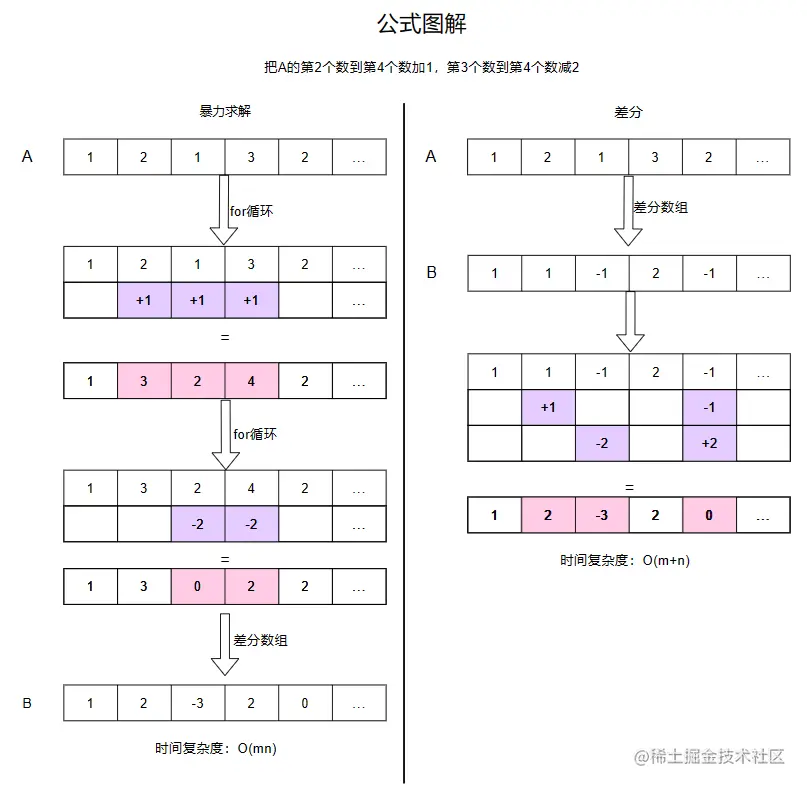
差分

原理

• 一维数组A
• 差分数组B
• 其中

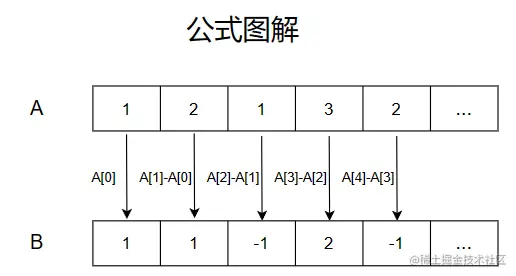
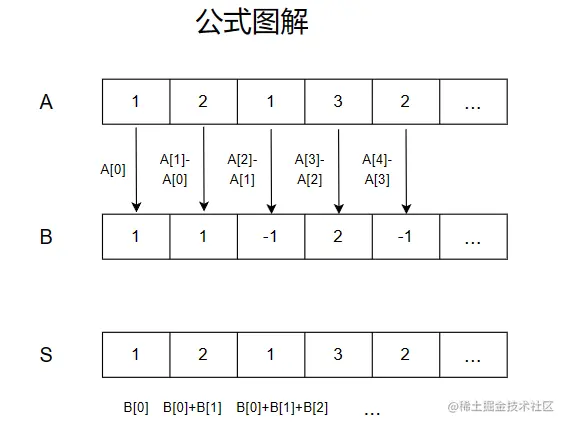
$B_1=A_1,B_i=A_i-A_{i-1}(2\leq i\leq n)$

• 差分数组B的前缀和数组就是原数组A

• 把A的第l个数到第r个数加d，B的变化为:

$B_l+d,B_{r+1}-d$

双指针扫描

双指针扫描

原理

用于解决一类基于“子段”的统计问题

子段:数组中连续的一段（下标范围可以用一个闭区间来表示)

这类题目的朴素做法都是两重循环的枚举，枚举左端点l、右端点r (l≤r)

优化手法都是找到枚举中的冗余部分，将其去除

优化策略通常有

• 固定右端点，看左端点的取值范围

  • 例如左端点的取值范围是一个前缀，可以用“前缀和”等算法维护前缀信息

• 移动一个端点，看另一个端点的变化情况

  • 例如一个端点跟随另一个端点单调移动，像一个“滑动窗口”
  • 此时可以考虑“双指针扫描”

时间复杂度

$O(n^2)$