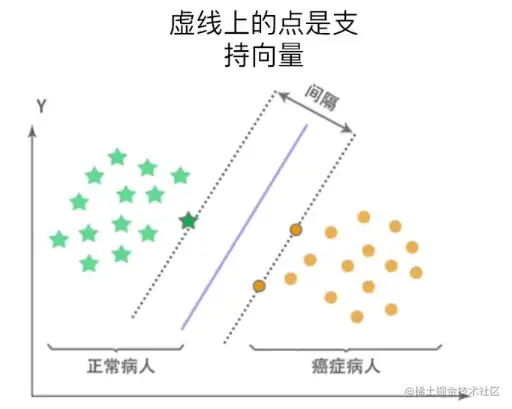
硬间隔SVM

• 训练集：${(x_1,y_1),(x_2,y_2),...,(x_n,y_n)},y_i \in \{-1,1\},i=1,2,...,n$
• 若训练集线性可分，通过最大化分类间隔得到分离超平面:$S= w^Tx+b$
• 决策函数为:$sign(w^Tx+b)$
• Hinge损失: $hinge(z) = max\{0,1- z\}$

软间隔SVM

• 如果数据线性不可分，增加松弛变量(Slack Variables)$\xi_i \ge 0$
• 目标函数

${min \atop\{w,b\}} \frac 1 2|w|^2+C\displaystyle\sum_{i=1}^n \xi_i$

s.t. $y_i(w^Tx_i+b)\ge1-\xi_i,i=1,2,...,n;$

$\xi_i\ge0,i=1,2,...,n$

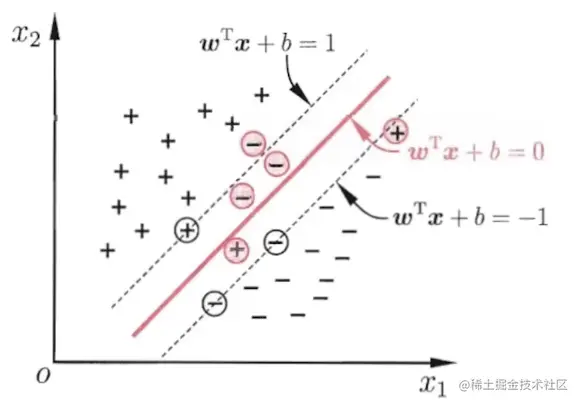
图片来源于周志华.机器学习.清华大学出版社，2016

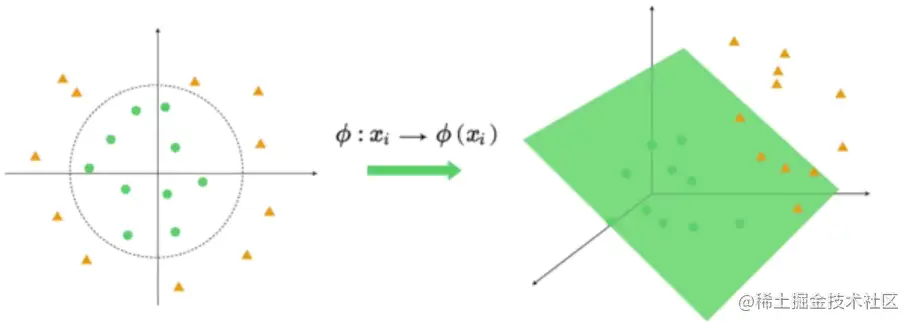
非线性SVM

• 若分类边界非线性，将样本从原始空间映射到一个更高维的特征空间，使样本在新的空间中线性可分。
• 特征$X_i$和$X_j$在新空间中的内积可以由它们在原始空间中通过核函数$k(X_i, X_j )$计算得到。

LinearSVC类

参数	说明
penalty	指定优化时使用的范数类型，默认为"l2"，可设置为"l1"
loss	指定优化时的损失函数，默认为"squared_ hinge"(平方合页损失)
C	设置惩罚系数，默认为1.0
multi_class	处理多分类问题的策略，默认为"ovr"(一对多)
class_weight	设置不同类别的分类权重

更多参数参考官方文档：scikit-learn.org/stable/modu…

构建线性支持向量机模型

from sklearn.svm import LinearSVC

# 模型构建与拟合
lsvm = LinearSVC()
lsvm.fit(train_x, train_y)