一、简介

为什么需要降维

数据的维度过高容易造成维数灾难（Curse of Dimensionality）。.

维数灾难：通常是指在涉及到向量的计算的问题中，随着维数的增加，计算量呈指数倍增长的一种现象。

这里可以举两个几何的例子来看一下维数过高的影响：

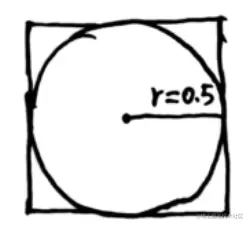
上图表示一个多维空间（以二维为例），则其中图形的体积有如下关系：

\begin{gathered} V_{\text {超立方体 }}=1 \\ V_{\text {超球体 }}=K \cdot 0.5^D \\ \lim _{D \rightarrow \infty} V_{\text {超球体 }}=0 \end{gathered}

上式也就表明当数据的维度过高时，数据主要存在于空间的边边角角的地方，这也就造成了数据的稀疏性。

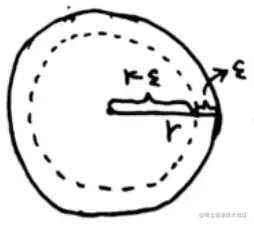
上图也表示一个多维空间 (以二维为例)，则其中图形的体积有如下关系:

\begin{aligned} & V_{\text {外 }}=K \cdot 1^D=K \\ & V_{\text {环形带 }}=V_{\text {外 }}-V_{\text {内 }}=K-K \cdot(1-\varepsilon)^D \\ & \frac{V_{\text {环形带 }}}{V_{\text {外 }}}=\frac{K-K \cdot(1-\varepsilon)^D}{K}=1-(1-\varepsilon)^D \\ & \lim _{D \rightarrow \infty} \frac{V_{\text {环形带 }}}{V_{\text {外 }}}=\lim _{D \rightarrow \infty} 1-(1-\varepsilon)^D=1 \\ & \end{aligned}

可以看到当数据的维度过高时，数据主要存在于球壳上，类似于人的大脑皮层。 2. 降维的方法降维可以作为一种防止过拟合的方式，其具体的方法包含下列几种:

特征选择是一种直接剔除主观认为不重要的特征的过程。

本文接下来的部分主要介绍主成分分析（PCA）。

二、样本均值与样本方差

概述

假设有以下数据：

\begin{gathered} x_i \in \mathbb{R}^p, i=1,2, \cdots, N \\ X=\left(x_1, x_1, \cdots, x_N\right)^T=\left(\begin{array}{c} x_1^T \\ x_2^T \\ \vdots \\ x_N^T \end{array}\right)=\left(\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 p} \\ x_{21} & x_{22} & \cdots & x_{2 p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{N 1} & x_{N 2} & \cdots & x_{N p} \end{array}\right)_{N \times p} \end{gathered}

样本均值与样本方差以下定义了数据的样本均值与样本方差:

\text { Sample Mean }: x_{p \times 1}^2=\frac{1}{N} \sum_{i=1}^N x_i\\ Sample Covariance : S_{p \times p}=\frac{1}{N} \sum_{i=1}^N\left(x_i-x^2\right)\left(x_i-x^2\right)^T

接下来需要对样本均值与样本方差进行一些变换来获得其另一种表示形式：

\begin{gathered} 规定向量 1_N=\left(\begin{array}{c}1 \\ 1 \\ \vdots \\ 1\end{array}\right)_{N \times 1}\\ x^2=\frac{1}{N} \sum_{i=1}^N x_i=\frac{1}{N} \underbrace{\left(\begin{array}{cccc} x_1 & x_2 & \cdots & x_N \end{array}\right)}_{X^T}\left(\begin{array}{l} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right)=\frac{1}{N} X^T 1_N \\ S=\frac{1}{N} \sum_{i=1}^N\left(x_i-x^2\right)\left(x_i-x^2\right)^T \\ 上式中 \left(x_1-x^2 \quad x_2-x^2 \quad \cdots \quad x_N-x^2\right)\\ =\left(\begin{array}{llll}x_1 & x_2 & \cdots & x_N\end{array}\right)-\left(\begin{array}{llll}x^2 & x^2 & \cdots & x^2\end{array}\right)\\ =X^T-x^2\left(\begin{array}{llll}1 & 1 & \cdots & 1\end{array}\right)\\ =X^T-x^2 1_N^T\\ =X^T-\frac{1}{N} X^T 1_N 1_N^T\\ =X^T\left(I_N-\frac{1}{N} 1_N 1_N^T\right)\\ 则 S=\frac{1}{N} X^T \underbrace{\left(I_N-\frac{1}{N} 1_N 1_N^T\right)}_H\left(I_N-\frac{1}{N} 1_N 1_N^T\right)^T X\\ ( H 称为中心矩阵, centering matrix)\\ =\frac{1}{N} X^T H H^T X \end{gathered}

中心矩阵 $H$ 具备以下性质：

\begin{gathered} & \text { (1) } H^T=H \\ & H^T=\left(I_N-\frac{1}{N} 1_N 1_N^T\right)^T=I_N-\frac{1}{N} 1_N 1_N^T=H \\ & \text { (2) } H^n=H \\ & H^2=H \cdot H=\left(I_N-\frac{1}{N} 1_N 1_N^T\right)\left(I_N-\frac{1}{N} 1_N 1_N^T\right) \\ & =I_N-\frac{2}{N} 1_N 1_N^T+\frac{1}{N^2} 1_N 1_N^T 1_N 1_N^T \\ & =I_N-\frac{2}{N}\left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right)\left(\begin{array}{llll} 1 & 1 & \cdots & 1 \end{array}\right)+\frac{1}{N^2}\left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right)\left(\begin{array}{llll} 1 & 1 & \cdots & 1 \end{array}\right)\left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right)\left(\begin{array}{llll} 1 & 1 & \cdots & 1 \end{array}\right) \\ & =I_N-\frac{2}{N}\left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \end{array}\right]_{N \times N}+\frac{1}{N^2}\left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \end{array}\right]_{N \times N}\left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \end{array}\right]_{N \times N} \\ & =I_N-\frac{2}{N}\left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \end{array}\right]_{N \times N}+\frac{1}{N^2}\left[\begin{array}{cccc} N & N & \cdots & N \\ N & N & \cdots & N \\ \vdots & \vdots & \ddots & \vdots \\ N & N & \cdots & N \end{array}\right]_{N \times N} \\ & =I_N-\frac{2}{N}\left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \end{array}\right]_{N \times N}+\frac{1}{N}\left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \end{array}\right]_{N \times N} \\ & =I_N-\frac{1}{N} 1_N 1_N^T \\ & =H \\ & \end{gathered}

因此最终可以得到

\begin{aligned} & x^2=\frac{1}{N} X^T 1_N \\ & S=\frac{1}{N} X^T H X \end{aligned}

三、主成分分析的思想

总结起来就是：

一个中心：PCA是对原始特征空间的重构，将原来的线性相关的向量转换成线性无关的向量；两个基本点：最大投影方差和最小重构距离，这是本质相同的两种方法，在接下来的部分将具体介绍。

PCA首先要将数据中心化（即减去均值）然后投影到一个新的方向上，这个新的方向即为重构的特征空间的坐标轴，同时也要保证投影以后得到的数据的方差最大，即最大投影方差，这样也保证了数据的重构距离最小。

四、最大投影方差

假设投影方向为 $u$ ，由于我们只关注投影的方向，因此将 $u$ 的模设置为 1 ，即 $u^T u=1$ ，则中心化后的数据在 $u$ 方向上的投影为 $\left(x_i-x^2\right)^T u$ ，是一个标量。按照最大投影方差的思想，我们定义损失函数如下:

\begin{gathered} J(u)=\frac{1}{N}\sum_{i=1}^{N}((x_{i}- \bar{x})^{T}u)^{2}\\ =\sum_{i=1}^{N}\frac{1}{N}u^{T}(x_{i}- \bar{x})(x_{i}- \bar{x} )^{T}u\\ =u^{T}\underset{S}{\underbrace{[\frac{1}{N}\sum_{i=1}^{N}(x_{i}- \bar{x})(x_{i}- \bar{x})^{T}]}}u\\ =u^{T}Su \end{gathered}

因此该问题就转换为以下最优化问题:

\left\{\begin{array}{c} \hat{u}=\underset{u}{\operatorname{argmax}} u^T S u \\ \text { s.t. } u^T u=1 \end{array}\right.

然后使用拉格朗日乘子法进行求解：

\begin{gathered} L(u, \lambda)=u^T S u+\lambda\left(1-u^T u\right) \\ \frac{\partial L}{\partial u}=2 S u-2 \lambda u=0 \\ S \underset{\text { 特征向量 }}{u}=\underset{\text { 特征值 }}{\lambda} u \end{gathered}

最后解得符合条件的向量是协方差矩阵 $S$ 的特征向量。如果想要降到 $q$ 维（ $q<p)$ ，则只需要将对应特征值最大的前 $q$ 个特征向量取出来作为投影方向然后获得数据在这些方向上的投影即为重构的坐标，即:

\left(\begin{array}{c} x_1^T \\ x_2^T \\ \vdots \\ x_N^T \end{array}\right)_{N \times p}\left(\begin{array}{llll} u_1 & u_2 & \cdots & u_q \end{array}\right)_{p \times q}=\left[\begin{array}{cccc} x_1^T u_1 & x_1^T u_2 & \cdots & x_1^T u_q \\ x_2^T u_1 & x_2^T u_2 & \cdots & x_2^T u_q \\ \vdots & \vdots & \ddots & \vdots \\ x_N^T u_1 & x_N^T u_2 & \cdots & x_N^T u_q \end{array}\right]_{N \times q}

特征向量表示投影变换的方向，特征值表示投影变换的强度。通过降维,我们希望减少冗余信息，提高识别的精度,或者希望通过降维算法来寻找数据内部的本质结构特征。找最大的特征值是因为，在降维之后要最大化保留数据的内在信息，并期望在所投影的维度上的离散最大。

五、最小重构距离

最小重构距离是另一种求解的方法，其本质上和最大投影方差是相同的。

我们知道有 $p$ 个投影方向符合条件，因此原来的数据可以表示为以下形式，降维的数据也就是舍弃掉第 $q+1$ 到第 $p$ 这几个方向上的信息。

$原来的中心化了的数据 x_i-x^2=\sum_{k=1}^p\left(\left(x_i-x^2\right)^T u_k\right) u_k\\ 降维的数据 \hat{x}_i=\sum_{k=1}^q\left(\left(x_i-x^2\right)^T u_k\right) u_k\\ \left(u_1\right. 到 u_p 分别对应从大到小的特征值)\\$

因此重构距离也就是指 $x_i-\hat{x}_i$ ，本着最小化重构距离的思想我们可以设置新的损失函数如下:

\begin{gathered} J=\frac{1}{N} \sum_{i=1}^N\left\|\left(x_i-x^2\right)-\hat{x}_i\right\|^2 \\ =\frac{1}{N} \sum_{i=1}^N\left\|\sum_{k=q+1}^p\left(\left(x_i-x^2\right)^T u_k\right) u_k\right\|^2 \\ =\frac{1}{N} \sum_{i=1}^N \sum_{k=q+1}^p\left(\left(x_i-x^2\right)^T u_k\right)^2 \\ =\sum_{k=q+1}^p \underbrace{\frac{1}{N} \sum_{i=1}^N\left(\left(x_i-x^2\right)^T u_k\right)^2}_{u_k^T S u_k} \\ =\sum_{k=q+1}^p u_k^T S u_k \\ \text { s.t. } u_k^T u_k=1 \end{gathered}

然后就可以转化为以下最优化问题:

\left\{\begin{array}{c} \hat{u}=\operatorname{argmin} \sum_{k=q+1}^p u_k^T S u_k \\ \text { s.t. } u_k^T u_k=1 \end{array}\right.

显然这里的每个 $u_k$ 是可以单独求解的，最终也可以解得 $u_k$ 是协方差矩阵 $S$ 的特征向量，只不过这里的 $u_k$ 是对应特征值较小的几个特征向量。

六、SVD角度看PCA和PCoA

协方差矩阵 $S$ 的特征分解:

S=G K G^T \text {, 其中 } G^T G=I, K=\left[\begin{array}{llll} k_1 & & & \\ & k_2 & & \\ & & \ddots & \\ & & & k_p \end{array}\right], k_1 \geq k_2 \geq \cdots \geq k_p

将 $X$ 中心化的结果 $H X$ 做奇异值分解:

H X=U \Sigma V^T \text {, 其中 }\left\{\begin{array}{l} U_{N \times N} \text { 是正交矩阵 } \\ V_{p \times p} \text { 是正交矩阵 } \\ \Sigma_{N \times p} \text { 是对角矩阵 } \end{array}\right.

接下里可以做以下变换：

\begin{aligned} S_{p \times p}= & X^T H X=X^T H^T H X=V \Sigma^T U^T U \Sigma V^T=V \Sigma^T \Sigma V^T \\ & \left(V \Sigma^T \Sigma V^T \text { 是 } S \text { 的特征值分解, } \Sigma^T \Sigma \text { 即为 } K \text { 。 }\right) \end{aligned}

接下来我们构造矩阵 $T_{N \times N}$ :

\begin{aligned} & T_{N \times N}=H X X^T H^T=U \Sigma V^T V \Sigma^T U^T=U \Sigma \Sigma^T U^T \\ & \left(U \Sigma \Sigma^T U^T \text { 是 } T \text { 的特征值分解, } \Sigma \Sigma^T \text { 为特征值矩阵。 }\right) \end{aligned}

对比 $S_{p \times p}$ 和 $T_{N \times N}$ ，我们可以发现: ①将 $S$ 进行特征分解然后得到投影的方向，也就是主成分，然后矩阵 $H X V$ 即为重构坐标系的坐标矩阵； ②将 $T$ 进行特征分解可以直拉获得坐标矩阵 $U \Sigma$ 。 (注意应保证 $S$ 和 $T$ 特征分解得到的特征向量是单位向量。)

关于为什么将 $T$ 进行特征分解可以直接获得坐标矩阵，现做以下解释:

$坐标矩阵HXV=U\Sigma V^{T}V=U\Sigma \\ 也就是说U\Sigma 即为坐标矩阵\\ 接着T{\color{Red} {U\Sigma}} =U\Sigma \Sigma^{T} U^{T}U\Sigma ={\color{Red} {U\Sigma}} (\Sigma^{T} \Sigma )\\ 也就是说U\Sigma是T的特征向量组成的矩阵$

使用 $T$ 进行特征分解的方法叫做主坐标分析 (Principal Co-ordinates Analysis，PCoA) 。这两种方法都可以得到主成分，但是由于方差矩阵是 $p \times p$ 的，而 $T$ 是 $N \times N$ 的，所以对样本量较少的时候可以采用 PCOA的方法。

七、概率PCA（p-PCA）

概述

假设有以下数据：

x \in \mathbb{R}^p, z \in \mathbb{R}^q, q<p

其中 $x$ 是原始数据， $z$ 是降维后的数据，可以将 $z$ 看做隐变量 (latent variable)， $x$ 看做观测变量 (observed variable)，则p-PCA就可以看做生成模型。 $x$ 和 $z$ 满足以下关系:

\left\{\begin{array}{c} z \sim N\left(0_{q \times 1}, I_{q \times q}\right) \\ x=W z+\mu+\varepsilon \\ \varepsilon \sim N\left(0_{p \times 1}, \sigma^2 I_{p \times p}\right) \end{array}\right.

这是一个线性高斯模型，其中 $\varepsilon$ 是噪声， $\varepsilon$ 与 $z$ 是独立的。求解这个模型要经过两个阶段: ①inference: 求 $P(z \mid x)$ ②learning: 使用EM算法求解参数 $W 、 \mu, \sigma^2$ 。 $x$ 的生成过程如下:

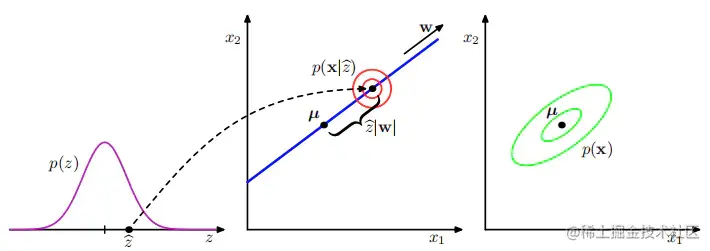
上图中数据空间为二维，潜在空间为一维。一个观测数据点 $x$ 的生成方式为: 首先从潜在变量的先验分布 $p(z)$ 中抽取一个潜在变量的值 $\hat{z}$ ，然后从一个各向同性的高斯分布 (用红色圆圈表示) 中抽取一个 $x$ 的值，这个各向同性的高斯分布的均值为 $W \hat{z}+\mu$ ，协方差为 $\sigma^2 I$ 。绿色椭圆画出了边缘概率分布 $p(x)$ 的密度轮廓线。 2. 推断 (inference) 求解 $P(z \mid x)$ 的过程如下:

P(z) \rightarrow P(x \mid z) \rightarrow P(x) \rightarrow P(z \mid x)

求 $P(x \mid z)$

\begin{gathered} E[x \mid z]=E[W z+\mu+\varepsilon]=W z+\mu+0=W z+\mu \\ \operatorname{Var}[x \mid z]=\operatorname{Var}[W z+\mu+\varepsilon]=\sigma^2 I \\ \Rightarrow x \mid z \sim N\left(W z+\mu, \sigma^2 I\right) \end{gathered}

求 $P(x)$

$E[x]=E[Wz+\mu +\varepsilon ]=E[Wz+\mu ]+E[\varepsilon ]=\mu \\ Var[x]=Var[wz+\mu +\varepsilon ]=Var[Wz]+Var[\varepsilon ]=WW^{T}+\sigma ^{2}I\\ \Rightarrow x\sim N(\mu ,WW^{T}+\sigma ^{2}I)$
其中， $Var[Wz] = WW^{T}$ 是因为 $z$ 的均值为0，则方差自然是W方了

求 $P(z \mid x)$ 该问题和高斯分布(1.intro_math)中第六部分的问题是类似的。

$\begin{gathered} \left(\begin{array}{c} x \\ z \end{array}\right) \sim N\left(\left[\begin{array}{c} \mu \\ 0 \end{array}\right],\left[\begin{array}{cc} W W^T+\sigma^2 I & \Delta \\ \Delta^T & I \end{array}\right]\right) \\ \Delta=\operatorname{Cov}(x, z) \\ =E\left[(x-\mu)(z-0)^T\right] \\ =E\left[(W z+\mu+\varepsilon-\mu) z^T\right] \\ =E\left[(W z+\varepsilon) z^T\right] \\ =E\left[W z z^T+\varepsilon z^T\right] \\ =E\left[W z z^T\right]+E\left[\varepsilon z^T\right] \\ =W E\left[z z^T\right]+E[\varepsilon] E\left[z^T\right] \\ =W E\left[(z-0)(z-0)^T\right]+0 \\ ==W \operatorname{Var}[z] \\ =W \\ \text { 因此 }\left(\begin{array}{l} x \\ z \end{array}\right) \sim N\left(\left[\begin{array}{c} \mu \\ 0 \end{array}\right],\left[\begin{array}{cc} W W^T+\sigma^2 I & W \\ W^T & I \end{array}\right]\right) \end{gathered}$

利用高斯分布中第五部分的公式可以求解 $P(z \mid x)$ :

P(z \mid x) \sim N\left(W^T\left(W W^T+\sigma^2 I\right)^{-1}(x-\mu), I-W^T\left(W W^T+\sigma^2 I\right)^{-1} W\right)

学习（learning）

使用EM算法求解，这里不做展示，后续章节会讲解。

八、小结

降维是解决维度灾难和过拟合的重要方法，除了直接的特征选择外，我们还可以采用算法的途径对特征进行筛选，线性的降维方法以 PCA 为代表，在 PCA 中，我们只要直接对数据矩阵进行中心化然后求奇异值分解或者对数据的协方差矩阵进行分解就可以得到其主要维度。非线性学习的方法如流形学习将投影面从平面改为超曲面。

『白板推导系列笔记』5.数据降维