从 3D 世界到 2D 视图的映射称为观测变换(viewing transformation)。它在物体序渲染中扮演着重要角色,用于计算场景中每个物体在图像空间中的位置,与射线追踪刚好相反。
通常,将 3D 世界中的点投影到 2D 图像只适用于渲染线框(wireframe),即,只渲染物体的边。本章只考虑由 3D 线段构成的线框模型,实心物体渲染由后续章节讨论。

观测变换
观测变换把世界空间中的点映射到图像的像素上。这一过程涉及到许多方面:相机位置和取向(orientation)、投影类型、视场角(field of view)、图像分辨率等。大多数图形系统会把这一过程分解为下面三个变换:
- 相机变换(camera transformation, 也称 eye transformation),将世界空间(world space)变换到相机空间(camera space, 也称为 eye space),它把相机以合适的取向摆放到原点。这一变换仅依赖于相机的位置和姿态。
- 投影变换(projection transformation),将相机空间变换到规范可视体(canonical view volume),对相机空间中的点进行投影,使得所有可见点归一化到 [−1,1] 区间上。这一变换仅依赖于投影类型。
规范可视体也称为裁剪空间(clip space),其中的坐标也称为归一化设备坐标(normalized device coordinate)。
有些 API 使用术语 “viewing transformation” 来表示相机变换,具体情况需具体分析。
- 视口变换(viewport transformation, 也称 windowing transformation),将规范可视体变换到屏幕空间(screen space),把单位图像映射到像素坐标下想要的位置。这一变换仅依赖于输出图像的位置和尺寸。
屏幕空间中的坐标也称为像素坐标(pixel coordinate)。

视口变换
规范可视体(canonical view volume)就是一个立方体 [−1,1]3。在规范可视体中,相机朝着 −z 方向,视口变换(viewport transformation)将 x=−1、x=+1、y=−1、y=+1 分别映射到屏幕左边界、右边界、下边界、上边界,也就是将 [−1,1]2 映射到 [−0.5,nx−0.5]×[−0.5,ny−0.5],其中,图像分辨率为 nx×ny。

将 z 整合进来可得视口矩阵(viewport matrix):
Mvp=2nx00002ny0000102nx−12ny−101
它将点的坐标从规范可视体映射到屏幕空间:
xscreenyscreenzcanonical1=Mvpxcanonicalycanonicalzcanonical1
z 值可用来确定前后关系。
正交投影变换
对于正交投影,相机空间中的可视区域可推广为 [l,r]×[b,t]×[f,n],这也称为正交可视体(orthographic view volume),它由 6 个平面围成:左平面(left plane)、右平面(right plane)、下平面(bottom plane)、上平面(top plane)、远平面(far plane)、近平面(near plane)。
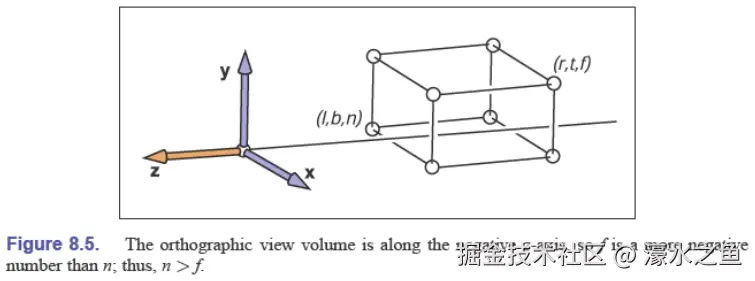
正交投影变换(orthographic projection transformation)可以将正交可视体变换为规范可视体:
Morth=r−l20000t−b20000n−f20−r−lr+l−t−bt+b−n−fn+f1
相机变换
下面这些信息可以确定观测者(viewer)的位置和姿态:
- 眼位(eye position)e
- 视向(gaze direction)g
- 向上向量(view-up vector)t
其中,t 是相机镜头垂直平分面上的任意向量。根据这些信息可以建立一个坐标系,原点为 e,基向量为 u、v、w。

相机变换(camera transformation)可以将规范坐标变换为相机坐标:
Mcam=[uxyz0vxyz0wxyz0exyz1]−1=xuxvxw0yuyvyw0zuzvzw00001100001000010−xe−ye−ze1
将三个变换结合起来,可以给出绘制 3D 线段的伪代码:
construct Mvpconstruct Morthconstruct McamM=MvpMorthMcamfor each line segment (ai,bi) dop=Maiq=Mbidrawline(xp,yp,xq,yq)
射影变换
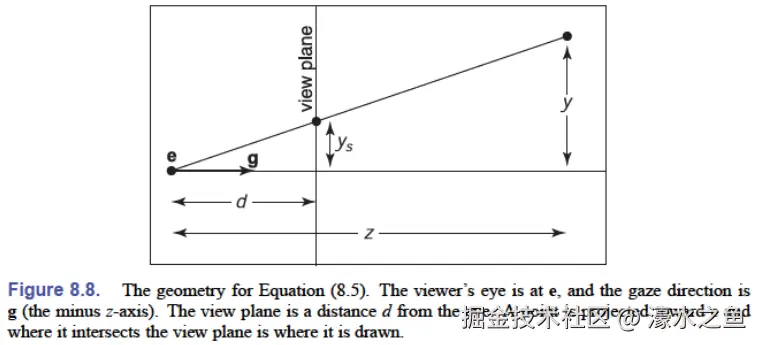
结合下图可知,透视投影满足:
ys=zdy
其中,d 是相机焦点到投影屏的距离。
虽然分式无法通过仿射变换来表示,但如果将齐次坐标的最后一个分量扩展为任意实数,并约定齐次坐标 [x,y,z,w]T 表示点 (x′,y′,z′)=(x/w,y/w,z/w),则齐次坐标的可逆线性变换:
x~y~z~w~=a1a2a3eb1b2b3fc1c2c3gd1d2d3hxyzw
对应非齐次坐标的分式线性变换(fractional linear transformation):
(x~′,y~′,z~′)=(x~/w~,y~/w~,z~/w~)
以 x~′ 为例:
x~′=ex′+fy′+gz′+ha1x′+b1y′+c1z′+d1
上式也称为关于 x′、y′、z′ 的线性有理函数(linear rational function)。
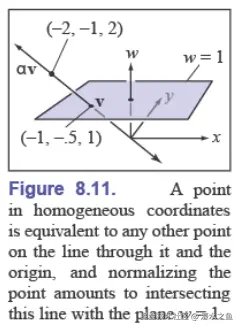
齐次坐标的可逆线性变换也称为射影变换(projective transformation,又名 homography)。实际上,上面对齐次坐标的约定正是射影几何中齐次坐标的原始定义。
射影空间可以通过高一个维度的线性空间来定义。使用非零数乘对线性空间中的向量建立等价关系:
x∼αx,∀ α=0
其中,x=[x1,x2,⋯,xn]T 称为齐次坐标,或齐次射影坐标。非零向量的等价类就是射影空间中的点,而非齐次坐标 (x1/xn,x2/xn,⋯,xn−1/xn) 可看作 xn=0 的等价类的一种表示。利用线性空间上的可逆线性变换可以定义射影空间上的变换:
A^xdefAx
其中,A 是线性空间中的可逆线性变换,A^ 是相应的射影变换,x 是向量 x 所属的等价类。根据线性代数的基础知识容易知道,上式确实给出了射影空间上的可逆变换,称为射影变换(projective transformation);而且 A^=λA,反之亦然,即同一个射影变换的齐次坐标表示之间最多差一个非零数乘。
据前文所述,射影变换可以表示非齐次坐标的分式线性变换,在一定条件下,这又可以退化为仿射变换。实际上,仿射变换就是一种特殊的射影变换,它将无穷远点/有限远点仍映射为无穷远点/有限远点,而透视投影之所以可以用射影变换来表示,是因为中心投影本身就是射影映射(projective mapping)。
射影变换可以构成一个群:
- A^B^=AB
- (A^B^)C^=A^(B^C^)
- I^A^=A^I^=A^
- A^−1=A−1
齐次坐标可以连续做多次射影变换或逆变换,而且可以随时通过齐次化(homogenize),即除以最后一个分量(如果非零),来获取当前等价类的非齐次坐标表示。
透视投影
透视投影仍采用近平面和远平面来限制可视范围。近平面作为投影平面(projection plane),像面距(image plane distance)为 −n。中心投影变换可以用透视矩阵(perspective matrix)来实现:
P=n0000n0000n+f100−fn0
透视矩阵有很多种选择,它们都会非线性地扭曲 z 值。
该矩阵对齐次坐标的作用如下:
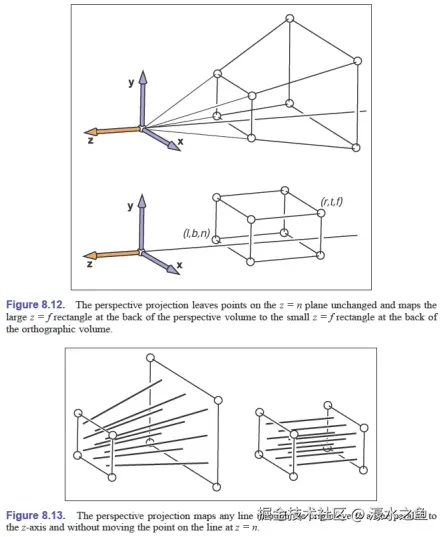
Pxyz1∼znxznyn+f−zfn1
由上式可知,矩阵 P 的选择保持了远平面上点的 z 值、近平面上的点,以及可视区域中 z 值的相对顺序。
由于数乘不改变射影变换,因此 P 的逆矩阵可以取为:
P−1=f0000f00000−100fnn+f
透视矩阵 P 只是将透视可视体(perspective view volume,也称为 frustum,即视锥体)映射为正交可视体。而透视投影矩阵(perspective projection matrix)将透视可视体变为规范可视体:
Mper=MorthP=r−l2n0000t−b2n00l−rl+rb−tb+tn−fn+f100f−n2fn0
不同的图形学 API 采用的规范略有不同,比如 OpenGL 中 n、f、zcanonical 与这里的正负号刚好相反,有些图形学 API 将规范可视体定为 [0,1]3,这些都会略微改变投影矩阵。
透视投影变换将线段映射为线段,进而将三角形映射为三角形、将平面映射为平面。实际上,任何矩阵 M 都会把线段 q+t(Q−q) 变换为 Mq+t(MQ−Mq)=r+t(R−r),齐次化后:
q、Q 是齐次化后的齐次坐标,表示变换前线段的起点和终点。
wr+t(wR−wr)r+t(R−r)=wrr+f(t)(wRR−wrr)其中,f(t)=wr+t(wR−wr)wRt
而透视投影矩阵 Mper 可以保证 f(t) 在 [0,1] 上单调增。
结合相机变换和视口变换可得透视观测变换:
M=MvpMorthPMcam
综上,绘制 3D 线段的伪代码如下:
compute Mvpcompute Mpercompute McamM=MvpMperMcamfor each line segment (ai,bi) dop=Maiq=Mbidrawline(xp/wp,yp/wp,xq/wq,yq/wq)
视场角
有时为简单起见,进一步约定:
l=−rb=−tnynx=tr
即,观测窗口中心在 z 轴上,而且图像没有变形。如果 nx、ny 已经确定,则仅剩一个自由度,一般用视场角(field-of-view,也称为视场)θ 来描述:
tan2θ=∣n∣t
这里的视场角也称为垂直视场角(vertical field-of-view)。
