《Fundamentals of Computer Graphics》第五版 第六章 线性代数

濠水之鱼
291 阅读3分钟

矩阵（matrix）是图形学程序中最常用的工具，它可以对点和向量进行变换（transform）。本章将从几何视角回顾基础的线性代数，主要关注几何直觉和算法，这些内容对二维、三维情形都适用。

行列式（determinant）

根据线性代数的基础知识，行列式具有以下基本性质：

  1. ∣A∣=∣AT∣|\mathbf{A}|=|\mathbf{A}^{T}|，其中 AT\mathbf{A}^{T} 是 A\mathbf{A} 的转置；
  2. ∣a⃗1⋯(ka⃗i)⋯a⃗n∣=k∣a⃗1⋯a⃗i⋯a⃗n∣|\vec{a}_{1}\cdots(k\vec{a}_{i})\cdots\vec{a}_{n}|=k|\vec{a}_{1}\cdots\vec{a}_{i}\cdots\vec{a}_{n}|，其中 kk 是任意常数；
  3. ∣a⃗1⋯a⃗i⋯a⃗j⋯a⃗n∣=−∣a⃗1⋯a⃗j⋯a⃗i⋯a⃗n∣|\vec{a}_{1}\cdots\vec{a}_{i}\cdots\vec{a}_{j}\cdots\vec{a}_{n}|=-|\vec{a}_{1}\cdots\vec{a}_{j}\cdots\vec{a}_{i}\cdots\vec{a}_{n}|；
  4. ∣a⃗1⋯(a⃗i+b⃗)⋯a⃗n∣=∣a⃗1⋯a⃗i⋯a⃗n∣+∣a⃗1⋯b⃗⋯a⃗n∣|\vec{a}_{1}\cdots(\vec{a}_{i}+\vec{b})\cdots\vec{a}_{n}|=|\vec{a}_{1}\cdots\vec{a}_{i}\cdots\vec{a}_{n}|+|\vec{a}_{1}\cdots\vec{b}\cdots\vec{a}_{n}|，其中 b⃗\vec{b} 是任意 nn 维列向量；
  5. ∣a⃗1⋯(a⃗i+ka⃗j)⋯a⃗n∣=∣a⃗1⋯a⃗i⋯a⃗n∣|\vec{a}_{1}\cdots(\vec{a}_{i}+k\vec{a}_{j})\cdots\vec{a}_{n}|=|\vec{a}_{1}\cdots\vec{a}_{i}\cdots\vec{a}_{n}|。

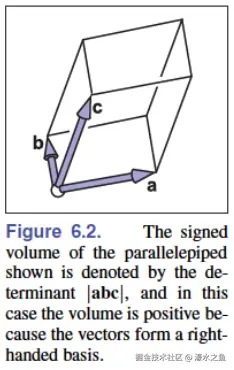
在几何上，行列式可以看作平行四边形（parallelogram）的有向面积（signed area）或者平行六面体（parallelepiped）的有向体积（signed volume）在任意维度的推广。平行四边形和平行六面体在任意维度的推广称为超平行体（parallelotope）。nn 维超平行体可以表示为：{ p⃗∈Rn ∣ p⃗=∑i=1ntia⃗i, 0⩽t1,⋯ ,tn⩽1 }\{\ \vec{p}\in\mathbb{R}^{n}\ |\ \vec{p}=\sum_{i=1}^{n}t_{i}\vec{a}_{i},\ 0\leqslant t_{1},\cdots,t_{n}\leqslant 1\ \}，a⃗1\vec{a}_{1}、a⃗2\vec{a}_{2}、…、a⃗n\vec{a}_{n} 是超平行体的棱向量。把上面的行列式基本性质和施密特正交化（Schmidt orthogonalization）结合起来可知，nn 维超平行体的体积正是行列式 ∣a⃗1a⃗2⋯a⃗n∣|\vec{a}_{1}\vec{a}_{2}\cdots\vec{a}_{n}| 的绝对值，因此行列式确实可以作为超平行体的有向体积；“体积正比于边长” 和 “切变不改变体积” 这两条性质，反映在行列式性质 2 和 5 中；而克拉默法则（Cramer's rule）也在一定程度上体现了 “切变不改变体积” 这一性质。

∑i=1nxia⃗i=[a⃗1,a⃗2,⋯ ,a⃗n]x⃗=y⃗⇒xi∣a⃗1⋯a⃗i⋯a⃗n∣=∣a⃗1⋯(xia⃗i)⋯a⃗n∣=∣a⃗1⋯∑i=1n(xia⃗i)⋯a⃗n∣=∣a⃗1⋯y⃗⋯a⃗n∣⇒xi=∣a⃗1⋯y⃗⋯a⃗n∣∣a⃗1⋯a⃗i⋯a⃗n∣\sum_{i = 1}^{n}x_{i}\vec{a}_{i} = [\vec{a}_{1}, \vec{a}_{2}, \cdots, \vec{a}_{n}]\vec{x} = \vec{y} \\ \begin{aligned} \Rightarrow x_{i}|\vec{a}_{1}\cdots\vec{a}_{i}\cdots\vec{a}_{n}| &= |\vec{a}_{1}\cdots(x_{i}\vec{a}_{i})\cdots\vec{a}_{n}| \\ &= |\vec{a}_{1}\cdots\sum_{i = 1}^{n}(x_{i}\vec{a}_{i})\cdots\vec{a}_{n}| \\ &= |\vec{a}_{1}\cdots\vec{y}\cdots\vec{a}_{n}| \end{aligned} \\ \Rightarrow x_{i} = \frac{|\vec{a}_{1}\cdots\vec{y}\cdots\vec{a}_{n}|}{|\vec{a}_{1}\cdots\vec{a}_{i}\cdots\vec{a}_{n}|}

二维、三维中有向体积的正负与棱向量组的手性（chirality）有关；如果棱向量组构成右手螺旋，则有向体积为正，反之为负。

signed-volumn.png

由于矩阵就是线性变换，因此行列式还可以理解为线性变换对体积的影响，雅可比行列式（Jacobian）就是一个很好的例子。

关于行列式的具体内容可以参考线性代数教材。

矩阵（matrix）

矩阵有数乘、加法、乘法运算：

kA=k(aij)r×c=def(kaij)r×cA+B=(aij)r×c+(bij)r×c=def(aij+bij)r×cAB=(aij)r×m(bij)m×c=def(∑l=1mailblj)r×ck\mathbf{A} = k(a_{ij})_{r\times c} \xlongequal{def} (ka_{ij})_{r\times c} \\ \mathbf{A} + \mathbf{B} = (a_{ij})_{r\times c} + (b_{ij})_{r\times c} \xlongequal{def} (a_{ij}+b_{ij})_{r\times c} \\ \mathbf{A}\mathbf{B} = (a_{ij})_{r\times m}(b_{ij})_{m\times c} \xlongequal{def} \left(\sum_{l=1}^{m}a_{il}b_{lj}\right)_{r\times c}

矩阵乘法一般不满足交换律（commutative law）和消去律（cancellation law）：

AB≠BAAB=AC ⇏ B=C\mathbf{A}\mathbf{B} \neq \mathbf{B}\mathbf{A} \\ \mathbf{A}\mathbf{B} = \mathbf{A}\mathbf{C} \ \nRightarrow\ \mathbf{B} = \mathbf{C}

但满足结合律（associative law）和分配率（distributive law）：

(AB)C=A(BC)A(B+C)=AB+AC(A+B)C=AC+BC(\mathbf{A}\mathbf{B})\mathbf{C} = \mathbf{A}(\mathbf{B}\mathbf{C}) \\ \mathbf{A}(\mathbf{B} + \mathbf{C}) = \mathbf{A}\mathbf{B} + \mathbf{A}\mathbf{C} \\ (\mathbf{A} + \mathbf{B})\mathbf{C} = \mathbf{A}\mathbf{C} + \mathbf{B}\mathbf{C}

单位矩阵（identity matrix）I\mathbf{I}：

I=def(δij)n×n其中，δij={1, i=j0, i≠j\mathbf{I} \xlongequal{def} (\delta_{ij})_{n\times n} \\ \text{其中，} \delta_{ij}= \left\{ \begin{aligned} &1,\ i=j \\ &0,\ i\neq j \end{aligned} \right.

方阵 A\mathbf{A} 的逆矩阵（inverse matrix）A−1\mathbf{A}^{-1}：

AA−1=A−1A=I\mathbf{A}\mathbf{A}^{-1} = \mathbf{A}^{-1}\mathbf{A} = \mathbf{I}

乘积矩阵的逆：

(AB)−1=B−1A−1(\mathbf{A}\mathbf{B})^{-1} = \mathbf{B}^{-1}\mathbf{A}^{-1}

矩阵 A\mathbf{A} 的转置（transpose）AT\mathbf{A}^{T}：

AT=(aij′)c×raij′=defaji\mathbf{A}^{T} = (a'_{ij})_{c\times r}\quad a'_{ij} \xlongequal{def} a_{ji}

乘积矩阵的转置：

(AB)T=BTAT(\mathbf{A}\mathbf{B})^{T} = \mathbf{B}^{T}\mathbf{A}^{T}

矩阵的行列式满足：

∣AB∣=∣A∣∣B∣∣A−1∣=1∣A∣∣AT∣=∣A∣|\mathbf{A}\mathbf{B}| = |\mathbf{A}||\mathbf{B}| \\ \left|\mathbf{A}^{-1}\right| = \frac{1}{|\mathbf{A}|} \\ \left|\mathbf{A}^{T}\right| = |\mathbf{A}|

向量也可以用矩阵来表示，现今最常用的方式是用 n×1n\times 1 矩阵表示 nn 维向量，这也称为列向量（column vector）；而向量的线性变换可以用方阵左乘来表示。

也可以用方阵右乘表示线性变换，此时向量需用 1×n1\times n 矩阵来表示，这称为行向量（row vector）。这两种表示之间的区别仅在于方阵互为转置，但方阵右乘的这种表示现今已不常用。

向量点乘的矩阵形式：

a⃗Tb⃗\vec{a}^{T}\vec{b}

向量的张量积（outer product）的矩阵形式：

a⃗b⃗T=(aibj)n×n\vec{a}\vec{b}^{T} = (a_{i}b_{j})_{n\times n}

向量的张量积也称为并矢（dyad）。

由于分块（partitioning）不影响矩阵乘积的结果，因此矩阵乘法有多种理解方式。下面是方阵左乘列向量的两种最常见的理解方式：

y⃗=Ax⃗=[r⃗1 Tr⃗2 T⋮r⃗n T]x⃗=[r⃗1⋅x⃗r⃗2⋅x⃗⋮r⃗n⋅x⃗]=[c⃗1c⃗2⋯c⃗n][x1x2⋮xn]=∑i=1nxic⃗i\begin{aligned} \vec{y} &= \mathbf{A}\vec{x} \\ &= \begin{bmatrix} \vec{r}_{1}^{\ T} \\ \vec{r}_{2}^{\ T} \\ \vdots \\ \vec{r}_{n}^{\ T} \end{bmatrix} \vec{x} = \begin{bmatrix} \vec{r}_{1}\cdot\vec{x} \\ \vec{r}_{2}\cdot\vec{x} \\ \vdots \\ \vec{r}_{n}\cdot\vec{x} \end{bmatrix} \\ &= \begin{bmatrix} \vec{c}_{1} & \vec{c}_{2} & \cdots & \vec{c}_{n} \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix} = \sum_{i=1}^{n}x_{i}\vec{c}_{i} \end{aligned}

同阶方阵相乘也有很多种理解方式：

AB=[r1Ar2A⋮rnA][c1Bc2B⋯cnB]=(riAcjB)n×n=A[c1Bc2B⋯cnB]=[Ac1BAc2B⋯AcnB]=[r1Ar2A⋮rnA]B=[r1ABr2AB⋮rnAB]=[c1Ac2A⋯cnA][r1Br2B⋮rnB]=∑i=1nciAriB\begin{aligned} \mathbf{A}\mathbf{B} &= \begin{bmatrix} \mathbf{r}^{\mathbf{A}}_{1} \\ \mathbf{r}^{\mathbf{A}}_{2} \\ \vdots \\ \mathbf{r}^{\mathbf{A}}_{n} \end{bmatrix} \begin{bmatrix} \mathbf{c}^{\mathbf{B}}_{1} & \mathbf{c}^{\mathbf{B}}_{2} & \cdots & \mathbf{c}^{\mathbf{B}}_{n} \end{bmatrix} = (\mathbf{r}^{\mathbf{A}}_{i}\mathbf{c}^{\mathbf{B}}_{j})_{n\times n} \\ &= \mathbf{A} \begin{bmatrix} \mathbf{c}^{\mathbf{B}}_{1} & \mathbf{c}^{\mathbf{B}}_{2} & \cdots & \mathbf{c}^{\mathbf{B}}_{n} \end{bmatrix} = \begin{bmatrix} \mathbf{A}\mathbf{c}^{\mathbf{B}}_{1} & \mathbf{A}\mathbf{c}^{\mathbf{B}}_{2} & \cdots & \mathbf{A}\mathbf{c}^{\mathbf{B}}_{n} \end{bmatrix} \\ &= \begin{bmatrix} \mathbf{r}^{\mathbf{A}}_{1} \\ \mathbf{r}^{\mathbf{A}}_{2} \\ \vdots \\ \mathbf{r}^{\mathbf{A}}_{n} \end{bmatrix} \mathbf{B} = \begin{bmatrix} \mathbf{r}^{\mathbf{A}}_{1}\mathbf{B} \\ \mathbf{r}^{\mathbf{A}}_{2}\mathbf{B} \\ \vdots \\ \mathbf{r}^{\mathbf{A}}_{n}\mathbf{B} \end{bmatrix} \\ &= \begin{bmatrix} \mathbf{c}^{\mathbf{A}}_{1} & \mathbf{c}^{\mathbf{A}}_{2} & \cdots & \mathbf{c}^{\mathbf{A}}_{n} \end{bmatrix} \begin{bmatrix} \mathbf{r}^{\mathbf{B}}_{1} \\ \mathbf{r}^{\mathbf{B}}_{2} \\ \vdots \\ \mathbf{r}^{\mathbf{B}}_{n} \end{bmatrix} = \sum_{i=1}^{n}\mathbf{c}^{\mathbf{A}}_{i}\mathbf{r}^{\mathbf{B}}_{i} \end{aligned}

这些矩阵分块的方式有助于从几何视角更直观地理解矩阵运算。

对角矩阵（diagonal matrix）：

D=def(diδij)n×n\mathbf{D} \xlongequal{def} (d_{i}\delta_{ij})_{n\times n}

对称矩阵（symmetric matrix）：

AT=A\mathbf{A}^{T} = \mathbf{A}

正交矩阵（orthogonal matrix）：

RTR=RRT=I\mathbf{R}^{T}\mathbf{R} = \mathbf{R}\mathbf{R}^{T} = \mathbf{I}

关于矩阵的详细内容可以参考线性代数教材。

计算

行列式可以理解为关于矩阵的标量函数。而行列式的几何意义则有助于建立平面的参数方程——在给定平面上三个点的条件下。计算行列式一般采用按行/列展开的方式，这实际上是拉普拉斯定理（Laplace's theorem）的一个特例：

∣A∣=∑i=1nalialic , 1⩽l⩽n|\mathbf{A}| = \sum_{i=1}^{n}a_{li}a^{c}_{li}\ ,\ 1\leqslant l\leqslant n

其中，alica^{c}_{li} 是 alia_{li} 的代数余子式（algebraic cofactor）。如果行列式为 00，则说明行/列向量线性相关（linearly dependent），否则线性无关（linearly independent）。

逆矩阵也可以使用行列式来计算：

A−1=1∣A∣A∗\mathbf{A}^{-1} = \frac{1}{|\mathbf{A}|}\mathbf{A}^{*}

伴随矩阵（adjoint matrix）：

A∗=(aij′)n×n , aij′=defajic\mathbf{A}^{*} = (a'_{ij})_{n\times n} \ ,\ a'_{ij} \xlongequal{def} a^{c}_{ji}

用这种方法对大矩阵求逆时很低效，但是图形学中矩阵规模通常较小。

图形学中经常遇到 nn 个方程、nn 个未知量的线性方程组：

Ax⃗=b⃗\mathbf{A}\vec{x} = \vec{b}

求解这一问题有很多方法，最合适的解法取决于矩阵 A\mathbf{A} 的规模和性质。图形学中通常 n⩽4n\leqslant 4，此时克拉默法则（Cramer's rule）是一种合适的方法：

xi=∣a⃗1⋯a⃗i−1y⃗a⃗i+1⋯a⃗n∣∣A∣A=[a⃗1⋯a⃗i−1a⃗ia⃗i+1⋯a⃗n]x_{i} = \frac{|\vec{a}_{1}\cdots\vec{a}_{i-1}\vec{y}\vec{a}_{i+1}\cdots\vec{a}_{n}|}{|\mathbf{A}|} \\ \mathbf{A} = [\vec{a}_{1}\cdots\vec{a}_{i-1}\vec{a}_{i}\vec{a}_{i+1}\cdots\vec{a}_{n}]

原文中关于线性方程组是否有解的表述——“Note that if |A| = 0, the division is undefined and there is no solution”——有误，行列式 ∣A∣|\mathbf{A}| 为 00 时，方程组仍然可以有解，甚至有无穷多解。

本征值（eigenvalue）与矩阵对角化（matrix diagonalization）

满足下面方程的非零向量 a⃗\vec{a} 称为本征向量（eigenvector），λ\lambda 称为本征值（eigenvalue）：

“eigenvalue” 和 “eigenvector” 也可译为特征值和特征向量。

Aa⃗=λa⃗\mathbf{A}\vec{a} = \lambda\vec{a}

也就是说，矩阵的作用不改变本征向量的方向。

求解下面的本征多项式可以得到所有本征值：

∣λI−A∣=0|\lambda\mathbf{I} - \mathbf{A}| = 0

阶数较低的矩阵可以通过求根公式计算，而阶数较高的矩阵只能通过数值方法计算。

实对称矩阵（real symmetric matrix）的本征值均为实数，而且一定可以被对角化（diagonalization）：

对角化也是一种相似变换。相似变换其实就是坐标系变换，即 P−1AP\mathbf{P}^{-1}\mathbf{A}\mathbf{P} 是 A\mathbf{A} 在 P\mathbf{P} 的列向量基下的表示。

A=QDQT\mathbf{A} = \mathbf{Q}\mathbf{D}\mathbf{Q}^{T}

其中，对角矩阵 D=diag(λ1,λ2,⋯ ,λn)\mathbf{D}=\mathrm{diag}(\lambda_{1}, \lambda_{2},\cdots,\lambda_{n}) 由矩阵 A\mathbf{A} 的所有本征值构成，而正交矩阵 Q\mathbf{Q} 中的每一列是对应位置的本征向量。矩阵对角化也称为本征值分解（eigenvalue decomposition）。

奇异值分解

奇异值分解（singular value decomposition, 简称为 SVD）是本征值分解从对称矩阵向非对称矩阵——甚至非方阵——的一种推广：

A=USVT\mathbf{A} = \mathbf{U}\mathbf{S}\mathbf{V}^{T}

其中，U\mathbf{U}、V\mathbf{V} 均为正交矩阵，且不必相等，它们的每一列被称为左、右奇异向量（singular vector），矩阵 S=diag(σ1,σ2,⋯ ,σn)\mathbf{S}=\mathrm{diag}(\sigma_{1}, \sigma_{2},\cdots,\sigma_{n}) 的对角元称为奇异值（singular value）。

根据实对称矩阵的本征值分解可以知道，对于任意实矩阵 A\mathbf{A}，均存在正交矩阵 U\mathbf{U} 使得：

AAT=UDUT⇒(UTA)(UTA)T=D\mathbf{A}\mathbf{A}^{T} = \mathbf{U}\mathbf{D}\mathbf{U}^{T} \Rightarrow (\mathbf{U}^{T}\mathbf{A})(\mathbf{U}^{T}\mathbf{A})^{T} = \mathbf{D}

上式说明 UTA\mathbf{U}^{T}\mathbf{A} 中任意两行正交，且 D\mathbf{D} 的对角元均非负。对 UTA\mathbf{U}^{T}\mathbf{A} 中所有非零行归一化，再扩充出一组完备正交基作为每一列，从而构成正交矩阵 V\mathbf{V}，最终可以得到矩阵 A\mathbf{A} 的奇异值分解。这里已经显现出奇异值的唯一性问题，为解决这一问题，一般约定奇异值均非负。

反之，若已知矩阵 A\mathbf{A} 的奇异值分解，则有：

AAT=US2UT\mathbf{A}\mathbf{A}^{T} = \mathbf{U}\mathbf{S}^{2}\mathbf{U}^{T}

即，矩阵 A\mathbf{A} 的奇异值是矩阵 AAT\mathbf{A}\mathbf{A}^{T} 本征值的算数平方根，左奇异向量是 AAT\mathbf{A}\mathbf{A}^{T} 的本征向量；同理，右奇异向量是 ATA\mathbf{A}^{T}\mathbf{A} 的本征向量。

avatar
文章
阅读
粉丝