问题描述
在2.4的文章中我们已经求出了一个可行的凸空间
convexS={(s1,l1min,l1max),(s2,l2min,l2max),...(sn,lnmin,lnmax)}
我们需要在这个凸空间内求解一条满足车辆动力学特性、边界约束的轨迹path
path={(s1,l1),((s2,l2),...((sn,ln)}
[s1,s2,...,sn]已知,实际上我们的决策变量为xx
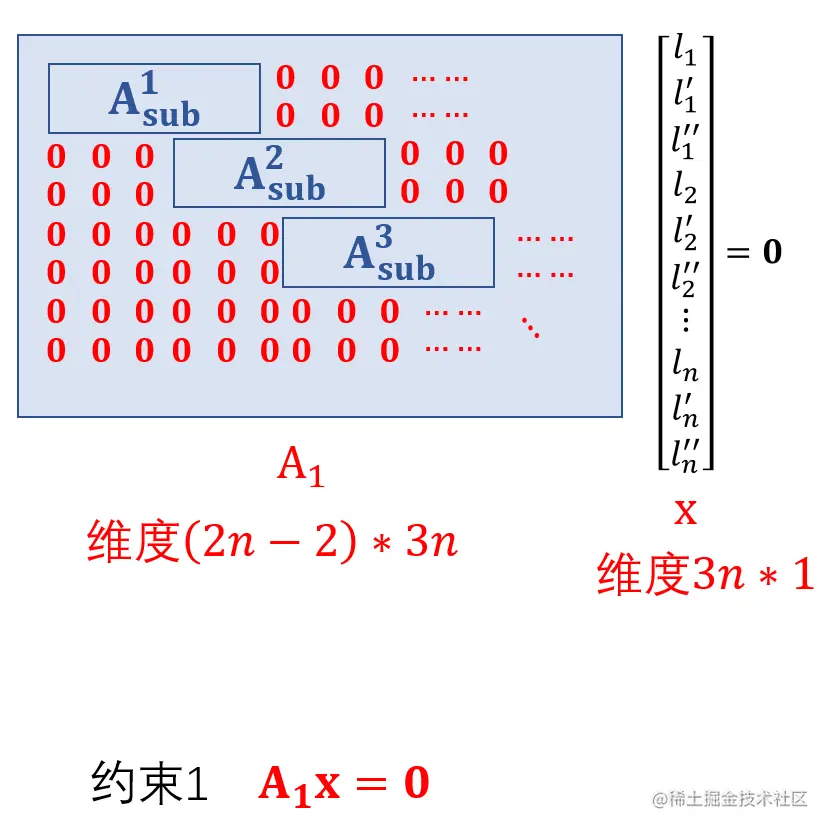
xx=[l1,l1′,l1′′,l2,l2′,l2′′,...,ln,ln′,ln′′]
约束条件
车辆动力学约束
这个约束的推导使用分段加加速度法,即认为在sl空间下,车辆的合理轨迹中:相邻的两个轨迹点之间的三阶导数为常数,即jerk为常数,4阶等更高阶的导数为0。
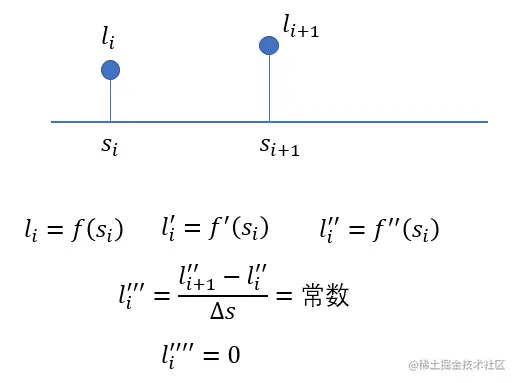
我们使用泰勒展开:

相邻点之间存在一次约束计算,共n−1次约束计算:
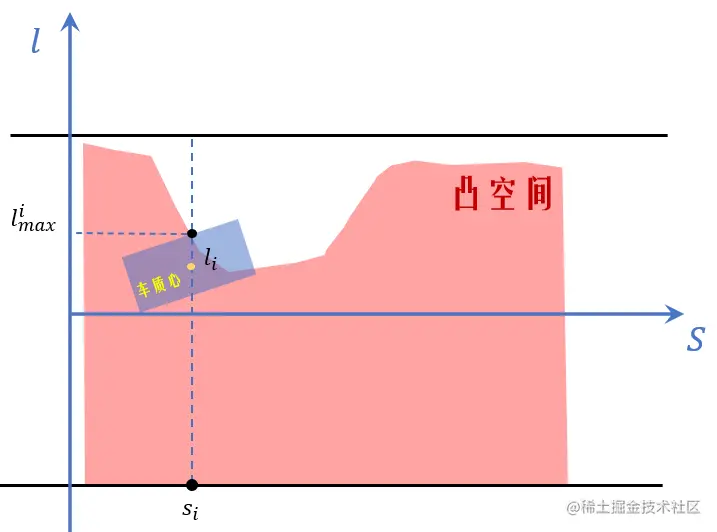
凸空间边界约束
边界约束要考虑车辆的形状,如果只考虑车辆中心点在凸空间内,无法保证整车均在凸空间范围内。
我们考虑车辆的形状为矩形
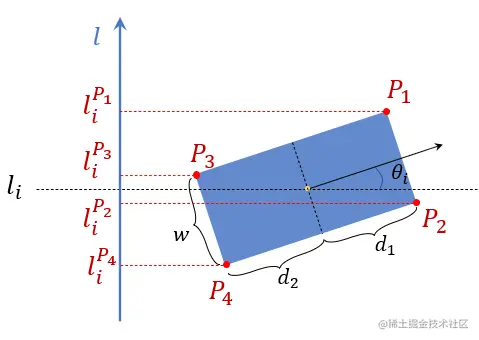
车辆中心的坐标为(si,li),考虑四个角点P1,P2,P3,P4的l坐标为liP1,liP2,liP3,liP4,依据的简单的几何关系我们可以得到下式(由于三角函数值是非线性的,我们做了偏于安全的近似处理)
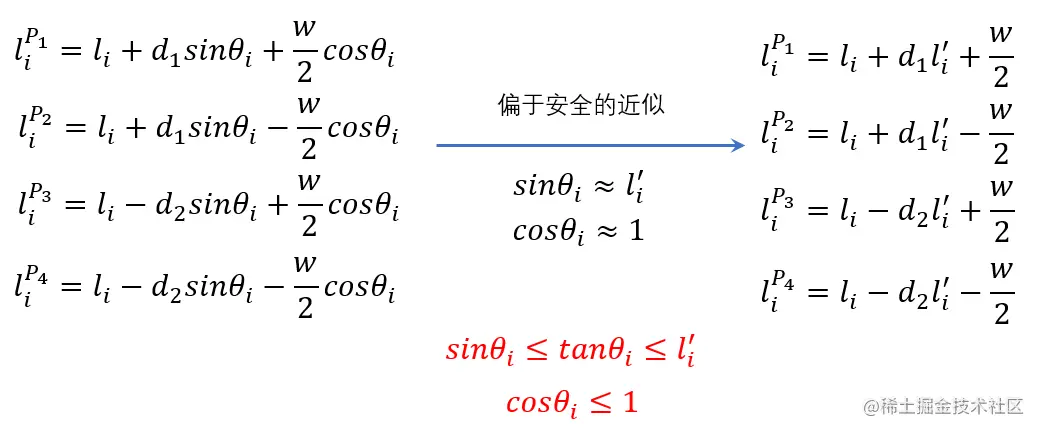
设P1,P2,P3,P4所处的s坐标附近的凸空间边界最大l值分别为:lbuip1,lbuip2,lbuip3,lbuip4,最小l值分别为:lblip1,lblip2,lblip3,lblip4,四个角点分别满足凸空间边界限制:

大于等于的不等式约束改为小于等于约束:
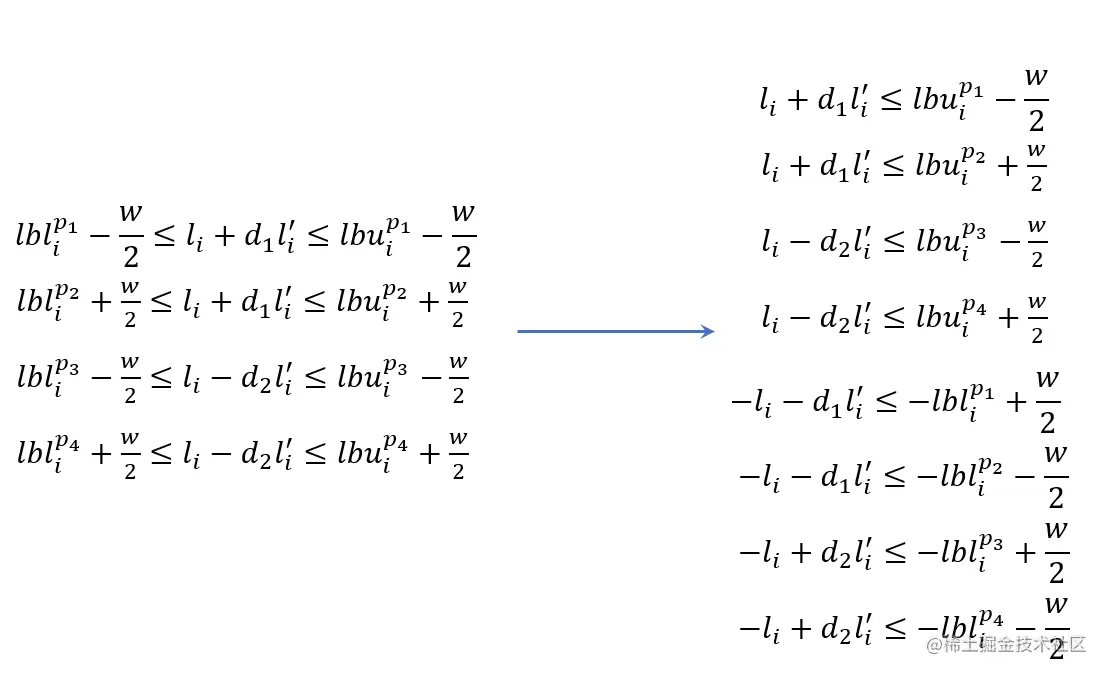
写为决策变量表示的矩阵形式:

每个轨迹点处有一个边界约束,共n个约束,使用矩阵形式表示:
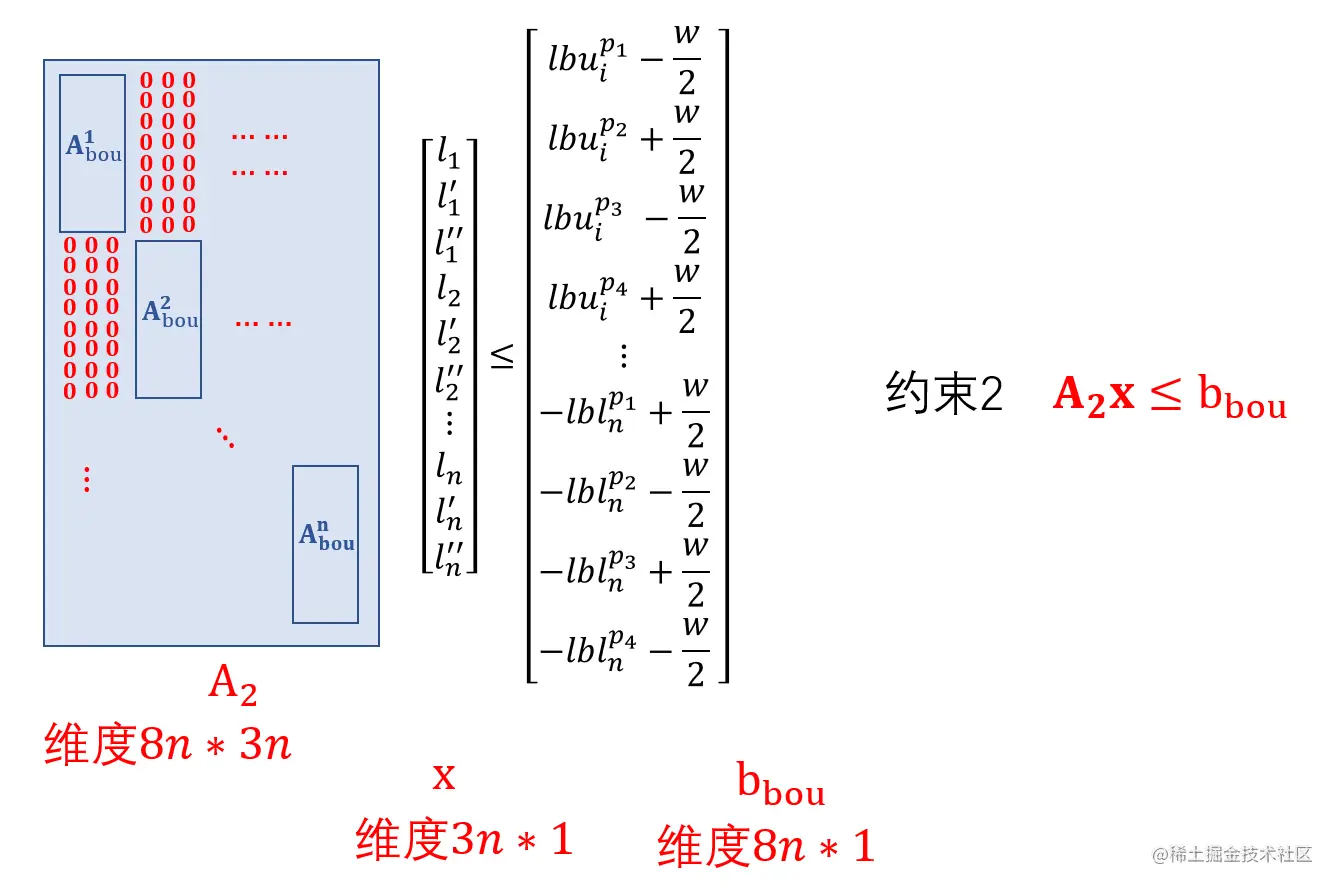
约束总结
因此我们的约束条件共有两个:
一个等式约束:
A1A1⋅xx=00
一个不等式约束:
A2A2⋅xx<=bboubbou
目标函数
参考线代价
轨迹点的li坐标代表了点到参考线的距离,所以参考线代价项:
costref=i=1∑nli2
 所以矩阵形式为:
所以矩阵形式为:
costref=xTxT⋅ArefAref⋅xx
平滑代价
平滑代价由一阶导数项、二阶导数项、三阶导数项构成:

一阶导数项、二阶导数项使用矩阵形式表达:
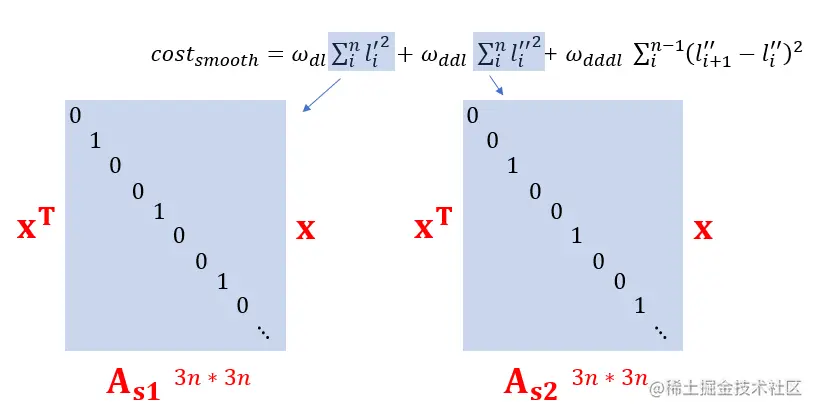
三阶导数项使用矩阵形式表达:
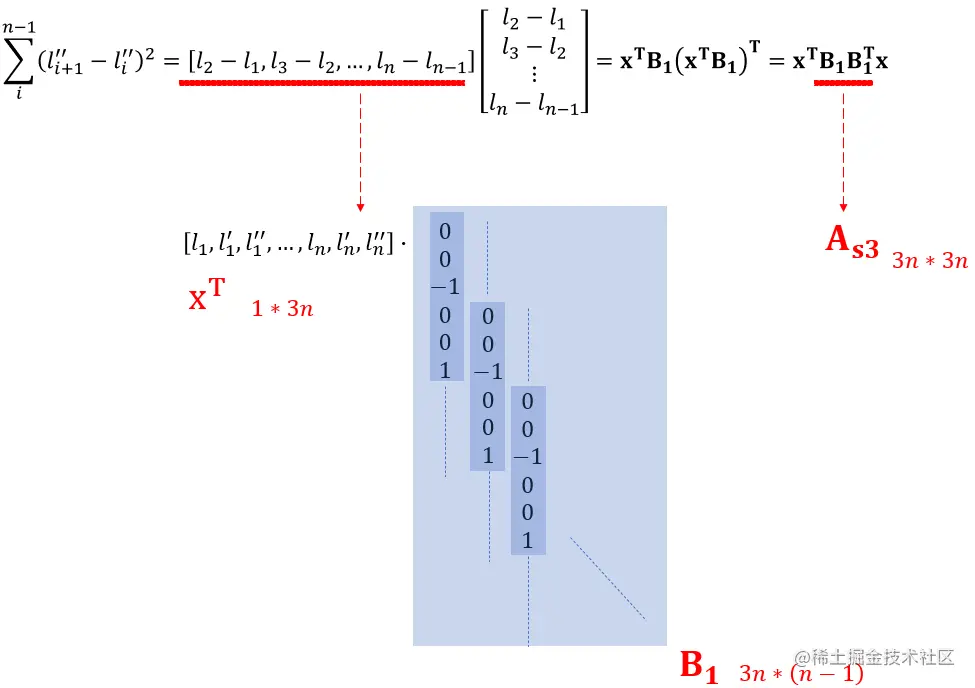
所以矩阵形式为:
costsmooth=xTxT⋅As1As1⋅xx+xTxT⋅As2As2⋅xx+xTxT⋅B1B1⋅xx
凸空间中心代价
我们希望车辆的轨迹不要离凸空间的中心线太远,所以设置了凸空间中心代价:
costcen=i=1∑n(li−2limax+limin)2
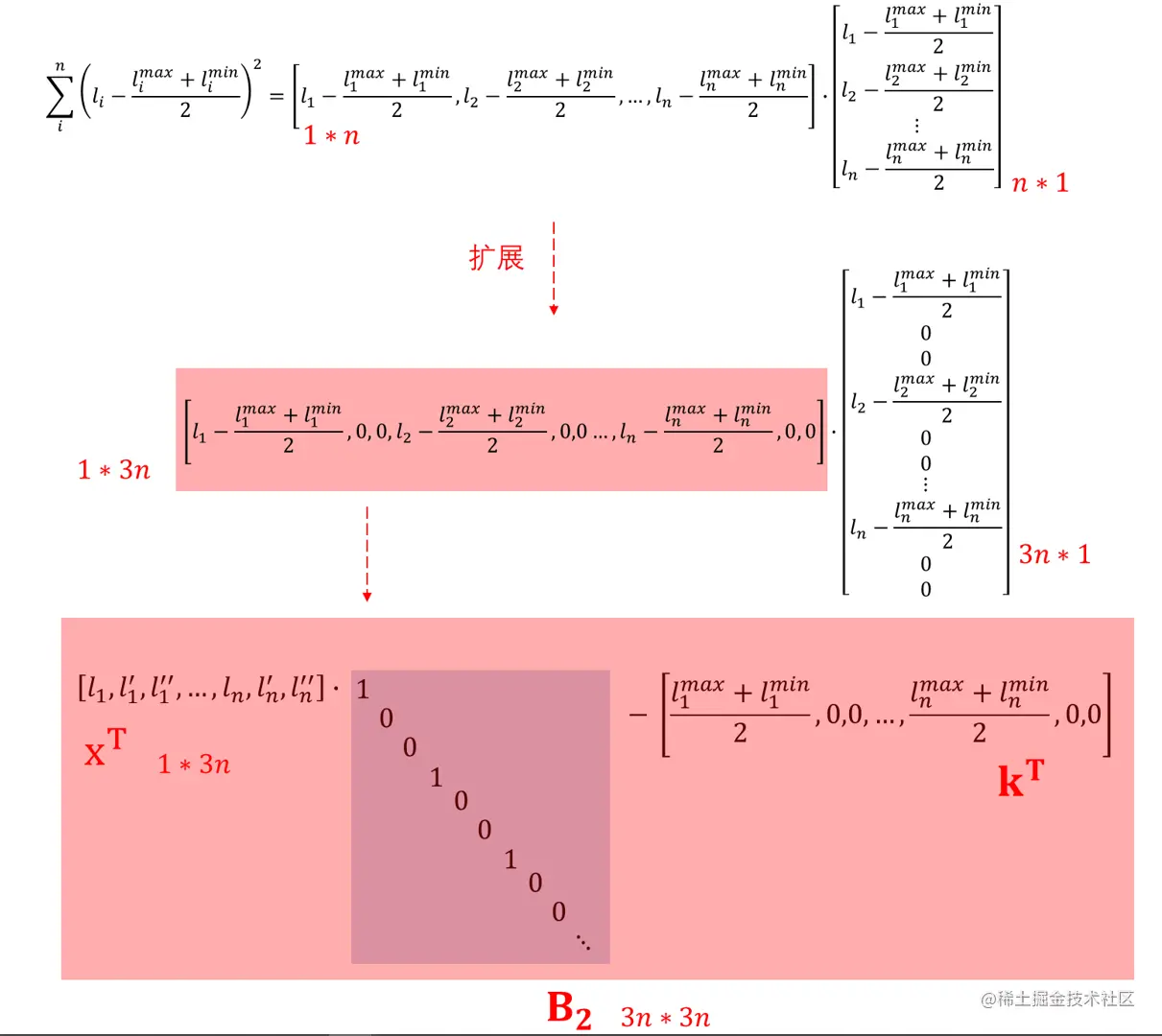

目标函数总结
由于二次规划问题的一般形式为:
min:21xTxT⋅HH⋅xx+fTfT⋅xxst:AA⋅xx<=bb,AeqAeq⋅xx=beqbeq,lblb<xx<ubub其中:xx,bb,beqbeq,lblb,ubub∈Rn,HH∈Rn∗n
在本文描述的问题中,参考线代价、平滑代价、凸空间中心代价构成了模型的目标函数:
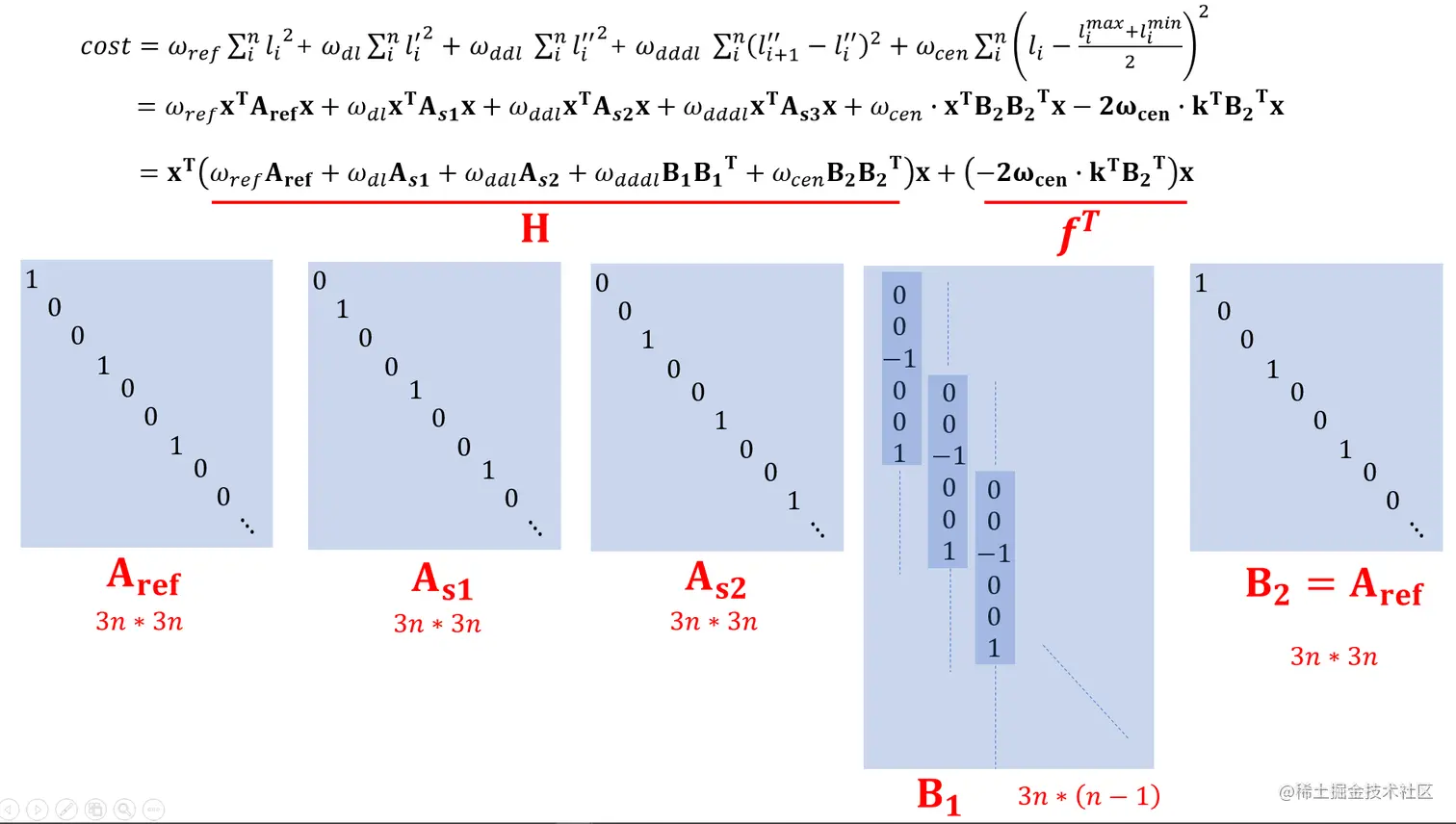
H、f的计算如上图所示,约束项矩阵、向量:
AeqAeq=A1A1beqbeq=00AA=A2A2bb=bboubbou
二次规划问题求解
直接使用matlab的二次规划求解函数或者python的二次规划求解函数即可。
代码实现
还没写完,写完更新。
参考来源
space.bilibili.com/287989852
所以矩阵形式为: