从复数到四元数资料援引复数的物理意义是什么？知乎视频-复数的物理意义视频-球极平面投影复球面——球极坐标平面投影

资料援引

复数的物理意义

我们都知道： $i^2 = -1$

那么可得： $4*i*i = -4$ ，其物理意义就是4在数轴上旋转了180度。

那么可推断出4*i就是旋转了90度。

不考虑i时，数的加减乘除仅能在实数轴上做运动，这是一维运动，而开始考虑i时，就诞生了一条虚数轴，这就允许点脱离线的限制，而存在于面上，这是二维运动。

可能读到这里你会觉得，唉？没什么了不起的啊， $（x，y）$ 也可以描述一个二维平面上的点啊。但是x、y是两个数描述一个二维点，而复数则是一个数描述一个二维点！

乘i即将向量转动90度：

首先了解两个概念：

模：复数的模等于复数描述的点到原点的距离。
辐角：复数的辐角等于复数描述的向量和x轴（实数轴）正半轴的夹角。

那么再来观察任意两个复数的乘积、模、辐角，可以发现：

两个复数乘积的模 = 两个复数模的乘积
两个复数乘积的辐角 = 两个复数辐角的和

球面投影

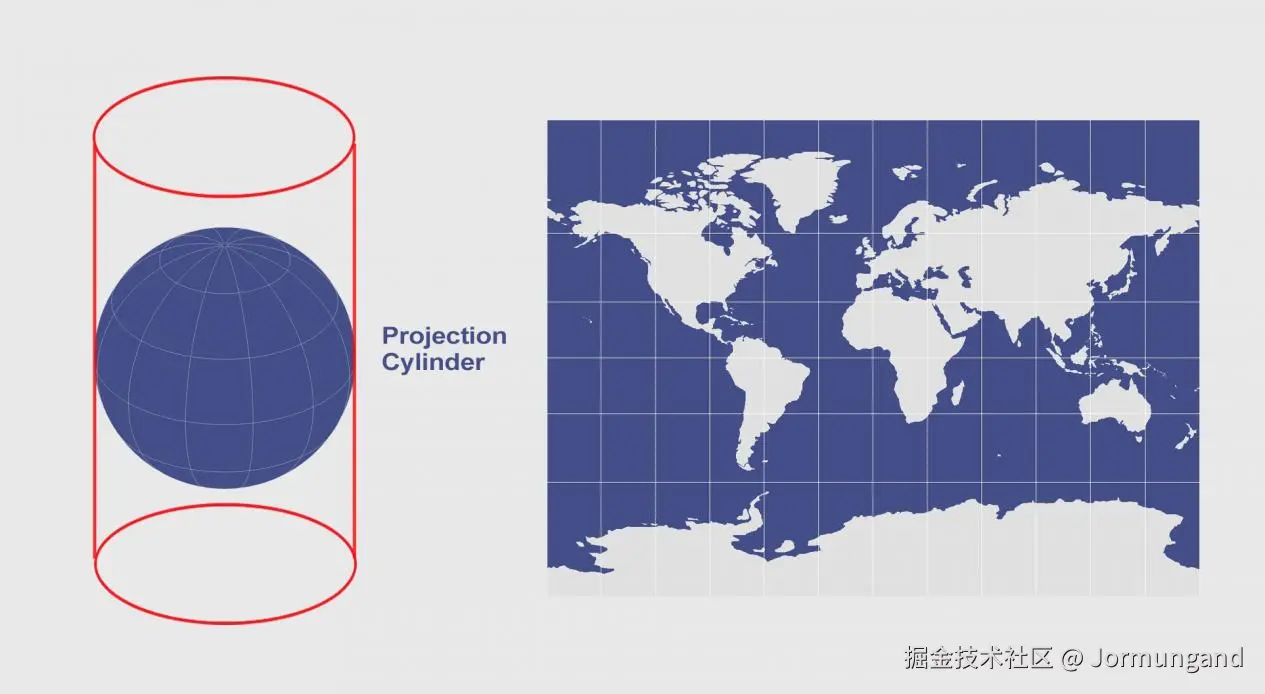
球面投影是指将球体表面上的点投影到一个平面的方法，主要有圆柱投影和球极平面投影两类方法。

圆柱投影

圆柱投影是一种将地球表面投影到一个圆柱体上，然后将圆柱体展开成平面的一种地图投影方法。根据圆柱体与地球的相对位置（如相切、相割）和投影特性的不同，圆柱投影可以分为多种类型，其中航海、航空等领域广泛应用的墨卡托投影就是其中的一种。

圆柱面包围投影球有三种可能的方式：

Equatorial：赤道模式，圆柱体的横截面与投影球的纬线平行
Transverse：横向模式，圆柱体的横截面与投影球的经线平行
Oblique：倾斜模式，包围方式为其它角度

问：为什么将球面展开成平面就是 2:1 ？

将球面展开成平面时，2:1 的比例是为了尽量减少变形和失真。这种展开方式通常被称为等距矩形投影（ Equirectangular Projection） ：

保持经纬比例关系：经度范围是0到360度（2π弧度），纬度范围是-90度到90度（π弧度）。因此，矩形的宽度是高度的两倍，即2:1的比例。
减少失真：虽然任何将球面展开成平面的投影都会引入某种形式的失真，但等距矩形投影在保持经纬度比例的同时，尽量减少了失真。这使得它在全景图和环境贴图中非常常用。
广泛应用：等距矩形投影广泛应用于全景图、虚拟现实（VR）、环境贴图等领域，因为它能够较好地表示球面上的信息，并且易于处理和渲染。

球极平面投影

取一球体，让它在坐标系原点与平面相切，相切点是它的南极：

将每个复数对应于球面上一点（除了北极，也就是投影的终点，没有复数与之对应，因为它对应于无穷远处）：

全部对应的结果：

为什么北极无法被投影在平面，只能对应无穷远？

首先复习一下两点式方程：

\cfrac{x-x_0}{x_0-x_1}=\cfrac{y-y_0}{y_0-y_1}=\cfrac{z-z_0}{z_0-z_1}

北极点三维坐标为 $（0,0,1)$ ，设球面上另一点的坐标为 $（x_1,y_1,z_1）$ ，可得两点式方程：

\cfrac{x}{-x_1}=\cfrac{y}{-y_1}=\cfrac{z-1}{1-z_1}

球的投影在二维平面上，因此需要令 $z=0$ ，可以解得 $\begin{cases}x=\cfrac{x_1}{1-z_1} \\ y=\cfrac{y_1}{1-z_1}\end{cases}$

可以得到表示三维球面坐标信息的复数方程式 $w = x + yi$

其中 $x$ 和 $y$ 对应二维坐标系中坐标， $x_1$ 、 $y_1$ 和 $z_1$ 对应三维坐标系中的坐标，由于分母不能为0，因此只有在 $z_1=1$ 时无法完成从三维坐标到二维坐标的转换，而整个球体只有北极点的 $z_1$ 为1。

这样球面就是一条复射影直线，它用一个复数表达式（ $w = x + yi$ ）来存储一个点的集合，集合中的点与球面上的位置一一对应，这些点组成了一根线，该线在二维平面上描述了一个三维球体，而不需要XYZ三维坐标来表达一个球体。
- 直线：数学上称点的集合为直线。
- 复直线：描述点的数都是复数。
- 射影：通过射影得到三维坐标在平面上对应的二维坐标，球上越靠近北极的点投影在平面上就离原点越远，直至趋近无穷。

球极平面投影完全保留了角度信息，但不维持面积不变，特别是在射影点附近。

二维空间的复数与旋转

欧拉公式

在体验复数是怎样实现二维空间旋转之前，首先有请宇宙第一耍帅公式欧拉公式隆重登场：

称它为宇宙第一耍帅公式是因为它的特殊形式——当x等于Pi的时候：

它将数学里最重要的几个数字联系到了一起：两个超越数：自然对数的底e，圆周率π；两个单位：虚数单位i和自然数的单位1；以及被称为人类伟大发现之一的0。

二维平面旋转公式(复数积型)

对于复数 $z=a+bi$ ， $a$ 对应实数轴上的距离， $b$ 对应虚数轴上的距离，该复数的模长 $r$ ：

r=\sqrt{a^2+b^2}

假设在平面上一个向量旋转的角度为θ， $z=a+bi$ 可以表达为：

z=rcosθ+i×rsinθ=r(cosθ+isinθ)

我们称括号中的内容为单位复数旋转因子，并用 $q$ 表示：

q=cosθ + isinθ

cosθ对应实数轴上的值，sinθ对应虚数轴上的值，以动图表示旋转因子与对应角度的关系：

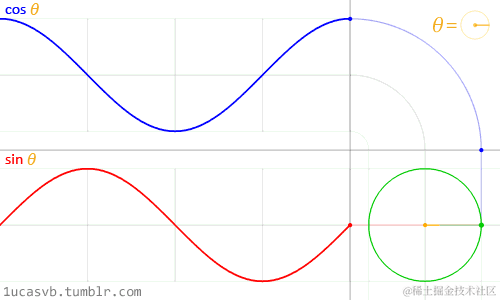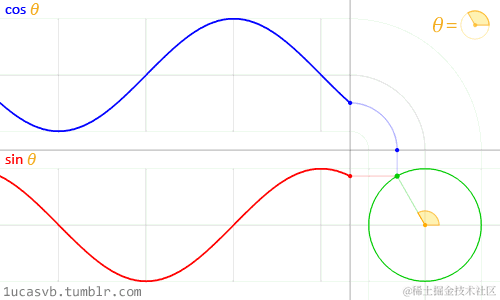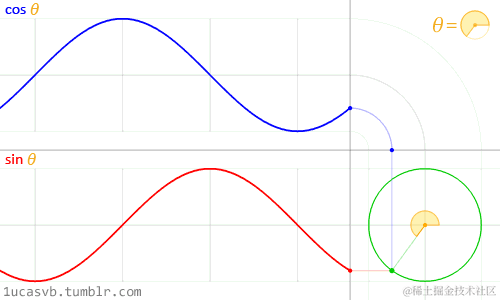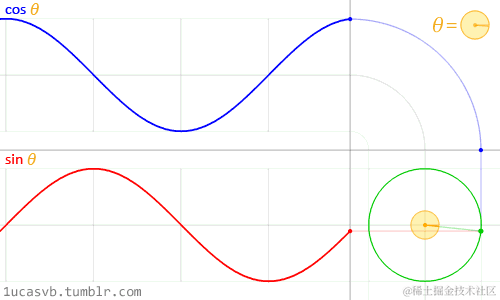
v2-29ad8022d279aa9b88da314ff8e6a448_b.webp.gif

假设被转动的向量以复数形式表达为 $p=a+bi$ ，将被转动的向量乘以这个单位复数旋转因子：

pq=(a+bi)(cosθ+isinθ)

得到被转动向量旋转θ后的复数p'，也就是二维平面旋转公式(复数积型)：

p'=pq=p(cosθ+isinθ)=acosθ-bsinθ+(asinθ+bcosθ)i

举个例子，比如被转动向量 $p=2+0i$ ，旋转角度为45度，所以最终得到的复数为：

p'=\sqrt{\smash[b]{2}}+\sqrt{\smash[b]{2}}i

也就是说起点坐标为 $(0,0)$ ，终点坐标为 $(2,2)$ 的向量，旋转45度之后终点坐标为 $(\sqrt{\smash[b]{2}},\sqrt{\smash[b]{2}})$ 。

因此将二维平面上一个向量 $（\overrightharpoon{a}，\overrightharpoon{b}）$ 看作复数 $a+bi$ ，再乘以单位复数旋转因子就可以实现旋转某个角度。

二维平面旋转公式(指数型/极坐标型)

$z=r(cosθ+isinθ)$ 还可以进行下一步的变形。根据欧拉公式：

cosθ + 𝑖sinθ = 𝑒^{𝑖θ}

将复数以极坐标形式表示为：

p=r𝑒^{𝑖θ}

现在复数的定义就与实部与虚部的两个分量 $𝑎、 𝑏$ 无关了，我们可以使用一个缩放因子 $𝑟$ 和旋转角度 $θ$ 的形式来定义任意一个复数，而且能更直观地理解复数旋转与缩放的性质，即：

两个复数乘积的模 = 两个复数模的乘积
两个复数乘积的辐角 = 两个复数辐角的和

如果仅需要旋转，而不需要放缩，那么可以令 $r=1$ ，得到二维平面旋转公式(指数型)：

p'=𝑒^{𝑖θ}p

四元数

由于三维空间比二维空间多了一维，为了实现类似的旋转，理所当然的想法就是在复数的基础上增加一个虚数 $j$ ，则三维空间里的复数定义为 $p=a+bi+cj$ 。

二维空间平面复数相乘以后会有-1代替 $i^2$ ，而三维复数多项式相乘完以后，必然会出现交叉乘积：ij、ji，这些乘积的结果可不是-1。

因此虚数的个数应该与维度无关（虚数个数 ${=}\mathllap{/\,}$ 维度-1），仔细想一下，在二维空间里复数的旋转轴是一维的，所以需要一个虚数i就可以，到了三维空间要想表示一个空间中的旋转轴就需要三维信息，所以除了i、j是不够的，还必须有k这个虚数（虚数个数=旋转轴维度），于是四元数就这样出现了，表达式为：

p=[s,v]

v代表i、j、k的多项式，对应于正常空间的三个维度，是虚数部；s代表实数部，对应于第四维：

p=s+xi+yj+zk

如何用i、j、k作为笛卡尔坐标系的单位向量：

四元数的乘积

两个四元数 $q_aq_b$ 的乘积：

q_{a}q_{b} = [s_{a},\mathbf {a}][s_{b},\mathbf {b}]

= (s_{a} + x_{a}\mathbf i + y_{a}\mathbf j +z_{a}\mathbf k)(s_{b} + x_{b}\mathbf i + y_{b}\mathbf j +z_{b}\mathbf k)

= (s_{a}s_{b} - x_{a}x_{b} - y_{a}y_{b} - z_{a}z_{b})

+ (s_{a}x_{b} + s_{b}x_{a} + y_{a}z_{b} - y_{b}z_{a})\mathbf i

+ (s_{a}y_{b}+s_{b}y_{a}+z_{a}x_{b}-z_{b}x_{a})\mathbf j

+ (s_{a}z_{b}+s_{b}z_{a}+x_{a}y_{b}-x_{b}y_{a})\mathbf k

将后3项和的多项式进行化简：前两列提取系数 $s_a$ 和 $s_b$ 作为公共部分，后两列直接写成ijk的虚数形式。并将加法展开再转换为[实数部,虚数部]的表达形式：

q_{a}q_{b} = [(s_{a}s_{b} - x_{a}x_{b} - y_{a}y_{b} - z_{a}z_{b}),

s_{a}(x_{b}\mathbf i + y_{b}\mathbf j+z_{b}\mathbf k) + s_{b}(x_{a}\mathbf i+y_{a}\mathbf j+z_{a}\mathbf k)

+(y_{a}z_{b}-y_{b}z_{a})\mathbf i+(z_{a}x_{b}-z_{b}x_{a})\mathbf j+(x_{a}y_{b}-x_{b}y_{a})\mathbf k]

引入向量a、b：

a=x_ai+y_aj+z_ak

b=x_bi+y_bj+z_bk

a、b的数量积（点积）的推导过程如下，i、j、k满足以下特点：

ii=jj=kk=1，ij=ik=jk=0

可得：

a \bullet  b=(x_ai+y_aj+z_ak)  \bullet (x_bi+y_bj+z_bk)

=x_ax_bii+x_ay_bij+x_az_bik+y_ax_bji+y_ay_bjj+y_az_bjk+z_ax_bki+z_ay_bkj+z_az_bkk

=x_ax_b+y_ay_b+z_az_b

a、b的向量积（叉积）的推导过程如下，i、j、k满足以下特点：

i=j×k ； j=k×i ；k=i×j

k×j=–i ；i×k=–j ；j×i=–k

i×i=j×j=k×k=i×j×k=0 （0是指0向量）

可得：

a ×  b=(x_ai+y_aj+z_ak)  × (x_bi+y_bj+z_bk)

=x_ax_bii+x_ay_bij+x_az_bik+y_ax_bji+y_ay_bjj+y_az_bjk+z_ax_bki+z_ay_bkj+z_az_bkk

=x_ay_bk-x_az_bj-y_ax_bk+y_az_bi+z_ax_bj-z_ay_bi

=(y_az_b-y_bz_a)i+(z_ax_b-z_bx_a)j+(x_ay_b-x_by_a)k

将a、b的带入到 $q_aq_b$ 的乘积结果中进行进一步化简，可得：

q_{a}q_{b} = [s_{a}s_{b} - \mathbf a\cdot \mathbf b, s_{a}\mathbf b + s_{b}\mathbf a + \mathbf a\times \mathbf b]

这就是四元数乘积的一般式。由于实际中要旋转的向量在三维空间，所以将 $q_a$ 看做是第四维（实数部）为0的纯四元数，则 $q_a=[0,a]$ 或 $q_a=(0+x_ai+y_aj+z_ak)$ ，那么得到三维空间旋转公式：

q_aq_b=[-a⋅b, s_ba+a×b]

四元数与三维空间旋转

三维空间旋转数

参照二维平面的旋转数，定义三维空间的旋转（四元）数q，使要旋转的向量旋转θ度，v是单位化的转轴方向：

q = [\cos\theta, \mathbf{v} \sin\theta]

倘若 q 是单位四元数，满足 $∣q∣=1$ ，可得：

∣q∣=cos⁡^2θ+(sin⁡θ)^2=\sqrt1=1

因此，四元数 $q$ 的逆 $q^{-1}$ 为其共轭：

q^{−1}=\={q}

共轭四元数 $\={q}$ 是：

\bar{q} = [\cos\theta, -\mathbf{v} \sin\theta]

所以，对于单位四元数 $q$ ，其逆 $q^{-1}$ 是：

q^{-1} = [\cos\theta, -\mathbf{v} \sin\theta]

计算四元数q和向量p的积，首先把p写成纯四元数的形式：

p=[0,p]

计算旋转后的向量 $p'$ ：

p'=qpp^{-1}

引用三维空间旋转公式，旋转数 $q$ 对应 $q_b$ ，待旋转向量 $p$ 对应 $q_a$ ，应用上文提到的四元数乘积公式 $q_aq_b=[-a⋅b, s_ba+a×b]$ 可得：

p'=qp=[0,p][\cos\theta, \mathbf{v} \sin\theta]=[-p \cdot \mathbf{v}\sin\theta, \cos\theta p+p \times \mathbf{v} \sin\theta]

考虑一个特殊情形： $p$ 与 $v$ 正交（垂直）。这种情况下， $v⋅p=0$ 。所以上面的四元数就变成了纯四元数：

p'=qp=[0,cosθp+vsinθ×p]

值得注意的是， $p'=qp$ 和 $p'=pq$ 的最终结果是不一样的。因为ijk环是有顺序的，所以通过改变左右乘可以决定旋转方向是逆时针（ $p'=qp$ ）还是顺时针（ $p'=pq$ ）。

验证

验证上面公式的正确性，例如绕z轴（k轴）旋转45度，那么：

q=[\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}k]

选一个特殊的p，它和k轴正交，譬如把p放到i轴上，也就是：

p=[0,2i+0j+0k]

代入公式，由于i和k正交，因此它们的点积为0：

\mathbf p' = \mathbf q\mathbf p

= [\frac {\sqrt {2}}{2},\frac {\sqrt {2}}{2}\mathbf {k}] [0,2\mathbf {i}]

= [0,2\frac {\sqrt {2}}{2}\mathbf {i} + 2\frac {\sqrt {2}}{2}\mathbf {k}\times \mathbf {i}]

= [0, \sqrt {2}\mathbf {i} + \sqrt {2}\mathbf {j}]

如果 $p'=pq$ ，那么结果是 $[0,\sqrt{2}i+\sqrt{2}i×k]=[0,\sqrt{2}i-\sqrt{2}j]$ ，旋转的方向也就改变了。
$[0,\sqrt{2}i+\sqrt{2}j]$ 是一个绕了k轴转了45度的纯四元数，其向量部分的长度是：

\mathbf p' = \sqrt { \sqrt {2}^{2} + \sqrt {2}^{2} } = 2

用图像展示旋转过程，红色向量绕蓝色向量旋转45度得到黄色向量：

引入共轭四元数

待旋转向量不是纯四元数时需要引入共轭四元数

现在，考虑一个一般的四元数，即和p不正交的四元数。此时 $v\mathrlap{\,/}{=}k$ ，而是偏移45度：

\hat { \mathbf v } = \frac {\sqrt {2}}{2}\mathbf {i} + \frac {\sqrt {2}}{2}\mathbf {k}

\mathbf {p} = 2\mathbf {i}

q = [cos\theta , sin\theta \mathbf {\hat { \mathbf v }} ]

p = [0, \mathbf {p}]

代入三维空间旋转公式：

\mathbf p' = \mathbf q\mathbf p

= [cos\theta ,sin\theta \mathbf { \hat { \mathbf v } }] [0, \mathbf {p} ]

[-sin\theta \hat { \mathbf v }\cdot \mathbf {p}, cos\theta \mathbf {p}+sin\theta \mathbf { \hat { \mathbf v } }\times \mathbf {p}]

用相应的值替换对应变量：

p' = [-\frac {\sqrt {2}}{2}(\frac {\sqrt {2}}{2}\mathbf {i} + \frac {\sqrt {2}}{2}\mathbf {k} )\cdot (2\mathbf {i} ), \frac {\sqrt {2}}{2}2\mathbf {i} +\frac {\sqrt {2}}{2}(\frac {\sqrt {2}}{2}\mathbf {i} + \frac {\sqrt {2}}{2}\mathbf {k} )\times 2\mathbf {i} ]

= [-1, \sqrt {2}\mathbf {i} + \mathbf {j} ]

此时，计算结果已经不是纯四元数了，并且没有旋转45度、范数也不再是2（而是 $\sqrt{\smash[b]{3}}$ ）。用图像展示旋转过程：

严格来说，这样子在3维空间中表示 $p′$ 是不正确的。因为它是一个4维的向量！为了简单起见，这里只将这个四元数的向量部分显示出来。

如何将它变为纯四元数呢？Hamilton发现，如果对qp右乘q的逆，出来的结果是一个纯四元数，并且四元数向量部分的范数可以保持不变，验证一下：

\mathbf q = [cos\theta , sin\theta (\frac {\sqrt {2}}{2}\mathbf {i} + \frac {\sqrt {2}}{2}\mathbf {k})]

\mathbf q^{-1} = [cos\theta , -sin\theta (\frac {\sqrt {2}}{2}\mathbf {i} + \frac {\sqrt {2}}{2}\mathbf {k})]

这里 $q^{−1}=q^∗$ 是因为q是单位四元数。再代入 $θ=45^∘$ ，得到：

\mathbf q^{-1} = [\frac {\sqrt {2}}{2}, -\frac {\sqrt {2}}{2}(\frac {\sqrt {2}}{2}\mathbf {i} + \frac {\sqrt {2}}{2}\mathbf {k})]

\frac {1}{2}[\sqrt {2}, -\mathbf {i}-\mathbf {k}]

现在，把前面算出来的qp再次拿出来，进行四元数乘积运算：

\mathbf q\mathbf p = [-1, \sqrt {2}\mathbf {i} + \mathbf {j}]

qpq^{-1} = [-1, \sqrt {2}\mathbf {i} + \mathbf {j}]\frac {1}{2}[\sqrt {2}, -\mathbf {i}-\mathbf {k}]

= \frac {1}{2}[-\sqrt {2}-(\sqrt {2}\mathbf {i}+\mathbf {j})\cdot (-\mathbf {i}-\mathbf {k}), \mathbf {i}+\mathbf {k}+\sqrt {2}(\sqrt {2}\mathbf {i}+\mathbf {j})-\mathbf {i}+\sqrt {2}\mathbf {j}+\mathbf {k}]

= \frac {1}{2}[-\sqrt {2}+\sqrt {2},\mathbf {i}+\mathbf {k}+2\mathbf {i}+\sqrt {2}\mathbf {j}-\mathbf {i}+\sqrt {2}\mathbf {j}+\mathbf {k}]

= [0,\mathbf {i}+\sqrt {2}\mathbf {j}+\mathbf {k}]

这下是纯四元数了，并且它的范数是：

|\mathbf q\mathbf p\mathbf q^{-1}| = \sqrt {1^{2} + \sqrt {2}^{2} + 1^{2} } = \sqrt {4} = 2

这和原始的p的范数一致。用图像展示旋转过程：

仔细观察上图，可以发现红色向量绕紫色向量旋转了90度（而不是45度）到黄色向量，因此为了正确地让一个向量绕某个轴向量旋转某个角度，必须以目标角度的一半来计算：

q = [cos\frac {1}{2}\theta ,sin\frac {1}{2}\theta \mathbf { \hat { \mathbf v } }]

这就是旋转四元数的一般形式！

四元数插值LERP

SLERP可以在2个朝向之间平滑地插值。第一个朝向设为q1，第二个朝向设为q2（q1和q2是单位四元数）。被插值前的点设为p，插值后的点设为p′。而插值参数t，当t=0时会把p转到q1，当t=1时会转到q2。笛卡尔坐标系下（不是指四元数）的线性插值公式是：

q_t=Lerp(q_1, q_21, t)=q_1+(q_2-q_1)t

由于这样算出的 $q_t$ 不是单位四元数，所以需要对其进行归一化处理，也就是使用了归一化线性插值：

q_t=Nlerp(q_1,q_2,t)=\frac{q_1+(q_2-q_1)t}{∣q_1+(q_2-q_1)t∣}

这样虽然能保证 $q_t$ 是单位四元数了，但是并不能保证获得均匀的角速度，⻆速度首先会不断地增加，到t = 0.50之后会开始减速。

四元数插值SLERP

于是就有了球面线性插值Slerp方法，这种方法不对四元数 $q_1$ 和 $q_2$ 直接插值，而是对两者之间的夹角 $\theta$ 插值。

四元数的加减

和复数类似，四元数也可以被加减：

q_{a} = [s_{a},\mathbf {a}]

q_{b} = [s_{b},\mathbf {b}]

q_{a} + q_{b} = [s_{a} + s_{b},\mathbf {a} + \mathbf {b}]

q_{a} - q_{b} = [s_{a} - s_{b},\mathbf {a} - \mathbf {b}]

对于四元数来说，减法等价于计算两个四元数的角度差：

P_{diff}=q_1^{-1}q_2 （由q_1P_{diff}=q_2 推出）

将向量的球面插值用于四元数

球面线性插值的一般形式：

\mathbf q' = \mathbf q_{1}(\mathbf q_{1}^{-1}\mathbf q_{2})^{t}

球面线性插值的常用形式可以通过将向量的球面插值公式用于四元数得到。计算向量的球面插值的一般形式定义如下：

\mathbf v_{t} = \frac {sin((1-t)\theta )}{sin\theta }\mathbf v_{1} + \frac {sin(t\theta )}{sin\theta }\mathbf v_{2}

用图像表示如下：

这个公式可以原封不动地应用到四元数，从而得到四元数球面线性插值的常用形式：

\mathbf q_{t} = \frac {sin((1-t)\theta )}{sin\theta }\mathbf q_{1} + \frac {sin(t\theta )}{sin\theta }\mathbf q_{2}

但这个公式需要提供角度θ，可以通过q1和q2的点积得出角度θ： $θ=acos(q_1⋅q_2)$

注意事项

当q1和q2的角度差非常小，小到导致 $sinθ=0$ 时，此时分母为零。这种情况下，可以使用归一化线性插值，此时归一化线性插值的误差非常小，基本不会与真正的Slerp有什么区别。

如果四元数点积的结果是负值（q1和q2的夹角为钝角），那么后面的插值就会在4D球面上绕远路。为了解决这个问题，点积结果是负值时，将两个四元数的其中一个的系数和向量部分取反（并不会改变它代表的朝向），从而保证这个旋转走的是最短路径。

四元数插值SQUAD

slerp插值存在的问题

如果需要对多个四元数进行插值，对每一对四元数使用Slerp插值虽然能够保证每两个四元数之间的⻆速度是固定的，但是⻆速度会在切换插值的四元数时出现断点，或者说在切换点不可导。举个例子，有q0、q1、q2三个四元数，分别对q0q1、q1q2 使用Slerp插值，当qt=q1时，⻆速度会突然改变。因此SQUAD插值以牺牲固定⻆速度为条件，从而在插值曲线连续的基础上，让一阶甚至是高阶导数是连续的（曲线连续我们称为C0连续，达到一阶导数连续就叫做C1连续，在此基础上达到二阶导数连续叫做C2连续，以此类推）。

向量运用贝塞尔曲线

以向量序列的线性插值类比上面讲的内容：

这个曲线虽然是连续的，但是它的一阶导数（切线）在切换插值向量时都不是连续的。为了解决这个问题，最常使用的就是贝塞尔曲线。直接使用一个四次Bézier曲线（因为有五个点）来生成这个近似曲线。但是Bézier曲线只会经过初始点与最终点（插值），一般不会经过中间的控制点（近似），所以这样求出来的曲线虽然是可导的，但是插值曲线不会经过中间的三个向量：

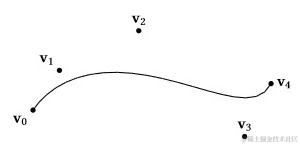
为了解决这个问题，可以分段对每两个向量vi和vi+1之间使用Bézier曲线进行插值，之后将所有的曲线连接起来。这就需要知道它们的前一个向量vi−1和后一个向量vi+2 ，通过这四个向量生成两个控制点si和si+1来控制曲线的趋势。此时，即可使用vi和vi+1作为端点，si和si+1作为中间控制点，使用一个三次Bézier曲线来近似这个两个向量之间的插值。如果想让最终的插值曲线达到C1连续，需要让前一个曲线在vi的控制点与当前曲线在vi的控制点分别处于最终曲线在vi处切线对等的两侧：

在上面的曲线中，蓝色的线就是曲线在点vi处的切线，红色的点就是三次Bézier曲线的控制点，分别处于切线对等的两侧。对于两个端点v0和v4，直接将这两个向量的控制点取为它们本身（这不是唯一的做法），最终得到一个平滑的曲线。

四元数运用贝塞尔曲线

如果有四元数序列：

\mathbf q_{1},\mathbf q_{2},\mathbf q_{3},\cdots,\mathbf q_{n-2},\mathbf q_{n-1},\mathbf q_{n}

需要让曲线的一阶导数连续，还需要知道前一个四元数 $q_{i-1}$ 和后一个向量 $q_{i+2}$ ，如此一来就可以在 $q_{i}$ 和 $q_{i+1}$ 之间使用贝塞尔曲线进行插值：

\mathbf q_{i-1},\mathbf q_{i},\mathbf q_{i+1},\mathbf q_{i+2}

使用上面四个四元数生成"辅助"四元数( $s_i$ 和 $s_{i+1}$ )，它们是中间控制点：

s_{i} = exp( - \frac {\log(\mathbf q_{i+1}\mathbf q_{i}^{-1})+\log(\mathbf q_{i-1}\mathbf q_{i}^{-1})}{4})\mathbf q_{i}

s_{i+1} = exp( - \frac {\log(\mathbf q_{i+2}\mathbf q_{i+1}^{-1})+\log(\mathbf q_{i}\mathbf q_{i+1}^{-1})}{4})\mathbf q_{i+1}

在t时刻的朝向就是：

squad(\mathbf q_{i}, \mathbf q_{i+1}, s_{i}, s_{i+1}, t ) = slerp(slerp(\mathbf q_{i}, \mathbf q_{i+1},t),slerp(s_{i},s_{i+1},t),2t(1-t))