预备知识

什么是自然坐标系

在笛卡尔坐标系下，以$x$轴坐标和$y$轴坐标确定一个点，$x$轴与$y$轴的方向是一直固定不变的,下图的$xy$轴，$y$轴的单位方向向量为(0,1),$x$轴的方向向量为(1,0)，即固定$xy$轴构成了确定一个坐标点位的参考系，而自然坐标系下的参考系不再是固定方向的，参考系是一条曲线，即下图红色曲线。

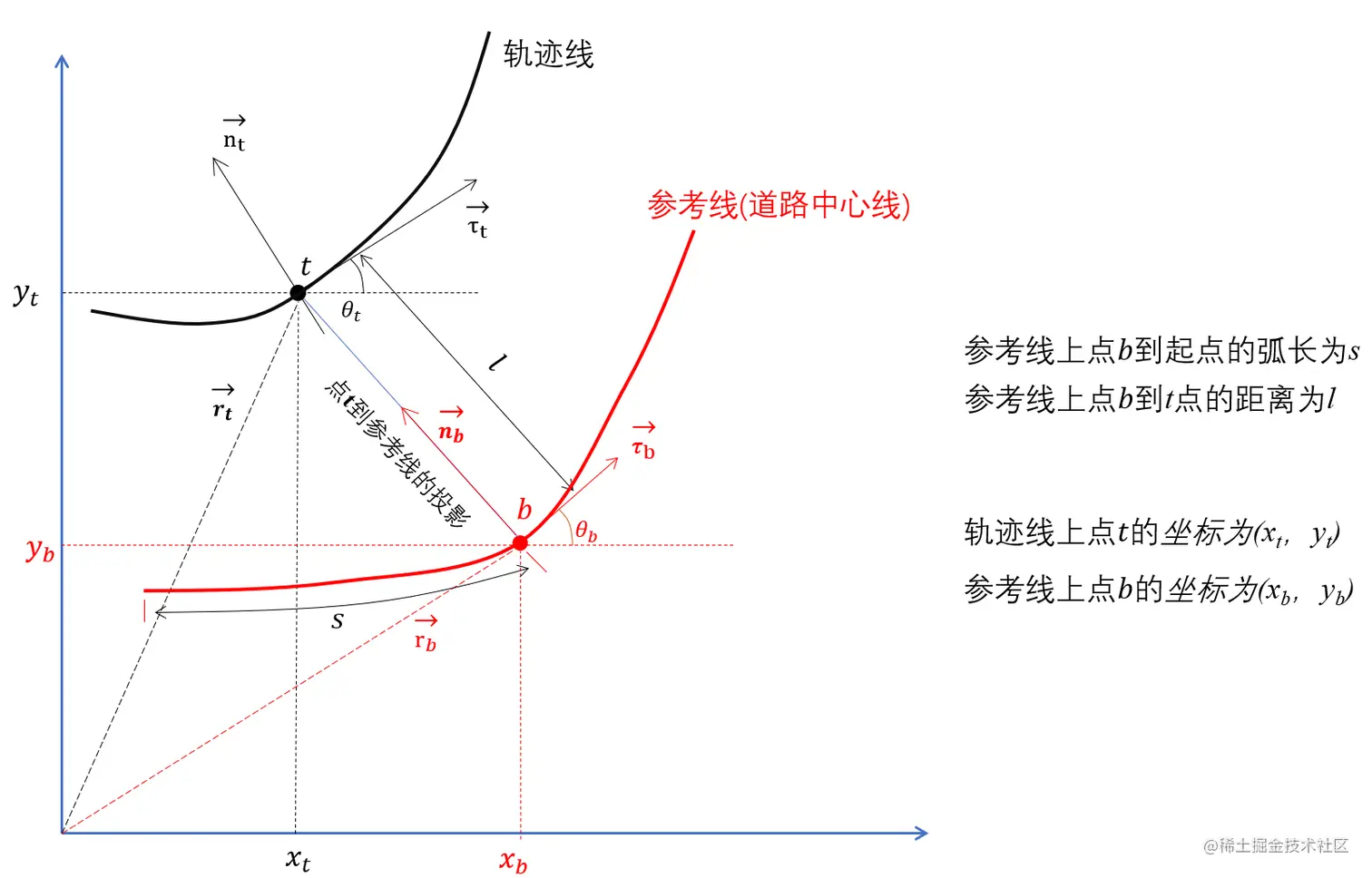
黑色曲线由车辆的轨迹点组成，现考虑某时刻的车辆轨迹点$t$，在笛卡尔坐标系下的坐标即为$(x_t,y_t)$,但是以笛卡尔坐标系描述车辆位置，在路径规划时不便于进行计算，需要将其投影到自然坐标系,进行横纵向的解耦。

下图以道路中心线作为自然坐标系的参考线，我们如何计算$t$点的自然坐标呢，首先找到$t$点在参考线上的投影点$b$，投影点$b$到参考线起点的弧长为$s$，$b$点到$t$点的距离为$l$，那么我们就称以参考线为参考系的$t$点的自然坐标为$(s,l)$

这样看来自然坐标和笛卡尔坐标还是比较相似的，只不过自然坐标系下两个轴的方向向量不是固定不变的，需要我们通过计算投影来获得两个轴的方向向量。

本文要讲解的就是基于指定条件笛卡尔坐标和自然坐标(Frenet坐标)的相互转化，有数学推导，不需要了解推导过程的可以直接看转换公式。

二维Frenet公式

Frenet公式有三维的表达形式，但是在自动驾驶领域，局部的道路路面看作是二维平面，不太关注高度信息，所以这里直接考虑二维的情况。

笛卡尔坐标系下，考虑曲线上一点，其位矢$\overrightarrow{r}$、单位法向量$\overrightarrow{n}$、单位切向量$\overrightarrow{\tau}$如下:

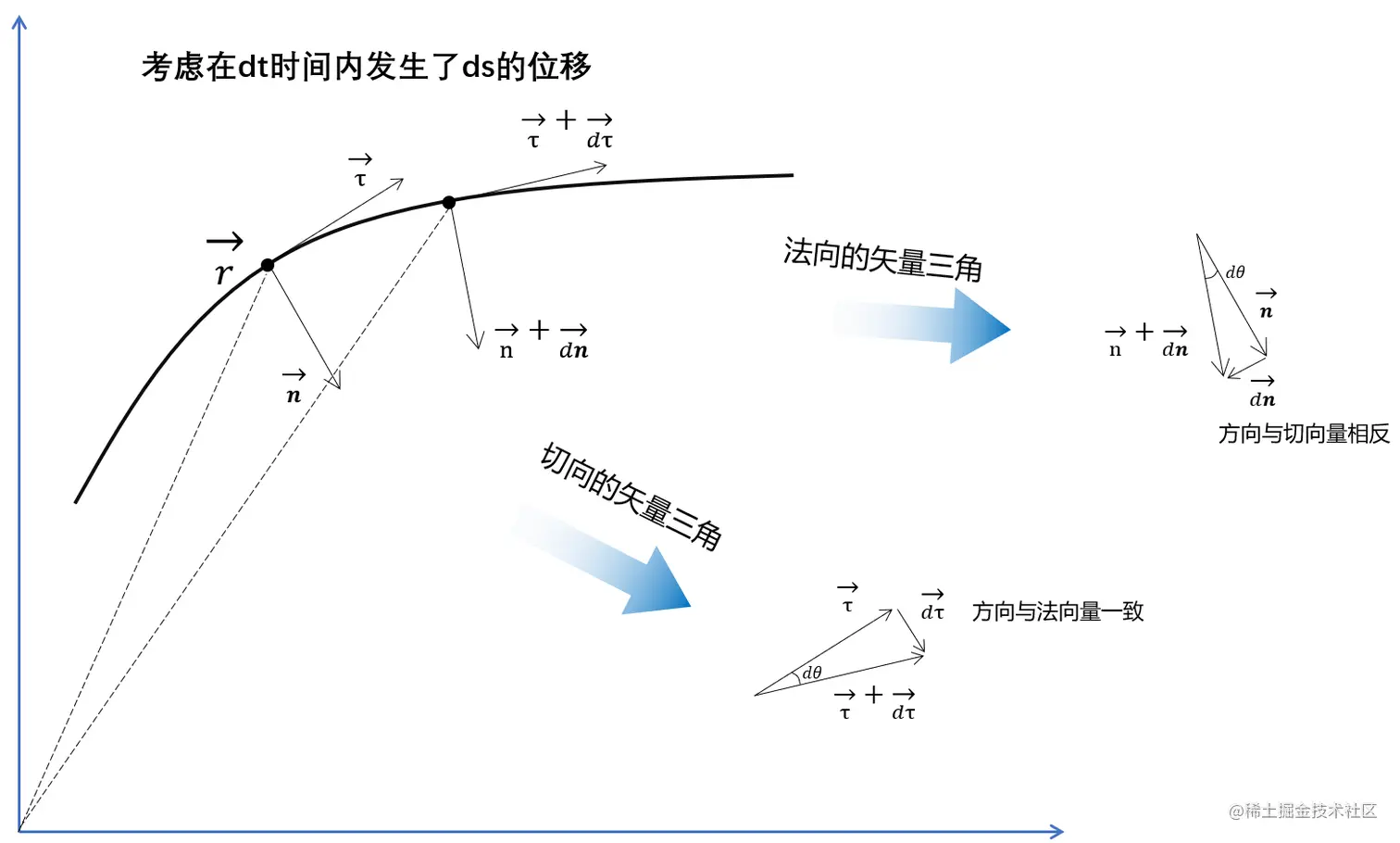
图1

1.求解切向量$\overrightarrow{\tau}$对弧长$s$的导数$\frac{d\overrightarrow{\tau}}{ds}$：

考虑点移动了一个微小的位移，转过$d\theta$，当$d\theta\rightarrow 0$，$d\overrightarrow{\tau}$的方向趋近于$\overrightarrow{\tau}$的垂直方向，与$\overrightarrow{n}$的方向一致，又$\overrightarrow{\tau}$+$d\overrightarrow{\tau}$，$d\overrightarrow{\tau}$都是单位向量，所以矢量三角是等腰三角形，有：

所以：

k为该点处的曲率。

2.求解法向量$\overrightarrow{n}$对弧长s的导数$\frac{d\overrightarrow{n}}{ds}$：

考虑指点移动了一个微小的位移，转过$d\theta$，当$d\theta\rightarrow 0$，$d\overrightarrow{n}$的方向趋近于$\overrightarrow{n}$的垂直方向，与$\overrightarrow{\tau}$的方向相反，所以有：

所以：

这里得到两个重要公式：

切向量和法向量对时间求导

链式转换一下：

曲线上点的速度和加速度公式(对时间求导)

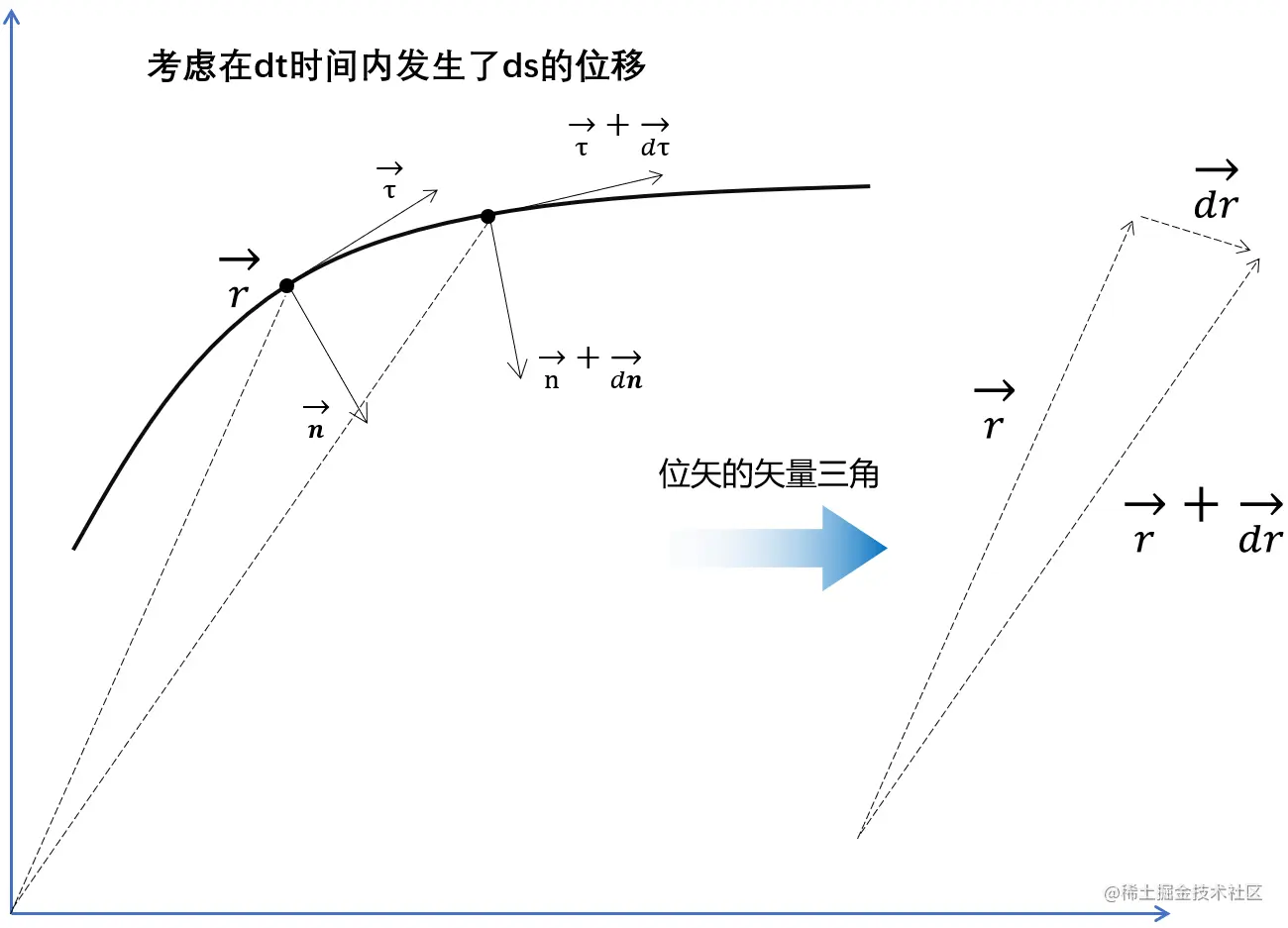
图2

在$d\overrightarrow{r}$趋近于0时,$d\overrightarrow{r}$的方向趋近于$\overrightarrow{\tau}$的方向，即切线方向，$|d\overrightarrow{r}|$趋近于$ds$：

位矢对时间的一阶导数即速度v：

位矢对时间的二阶导数即加速度a：

这里用到了乘法求导法则，同时用到了公式1的结论：

那么$\frac{d\overrightarrow{\tau}}{dt}$怎么求呢，要结合公式1的结论以及链式求导法则：

所以：

可以看出曲线上的点的加速度由切向加速度和法向加速度组成。

这一步得到两个重要基础公式：

预备知识总结

变量名称	含义
$\overrightarrow{r}$	曲线上某点在笛卡尔坐标系下的位矢
$\overrightarrow{\dot{r}}$	曲线上某点在笛卡尔坐标系下的速度向量($\overrightarrow{v}$)，对时间的导数
$\overrightarrow{\ddot{r}}$	曲线上某点在笛卡尔坐标系下的加速度向量($\overrightarrow{a}$)，对时间的导数
$\overrightarrow{\tau}$	曲线上某点在笛卡尔坐标系下的切向量(单位向量)
$\overrightarrow{n}$	曲线上某点在笛卡尔坐标系下的法向量(单位向量)
$\frac{d\overrightarrow{\tau}}{ds}$	曲线上某点的单位切向量对弧长的一阶导数
$\frac{d\overrightarrow{n}}{ds}$	曲线上某点的单位法向量对弧长的一阶导数
$\overrightarrow{\dot{\tau}}$	曲线上某点的单位切向量对时间的一阶导数
$\overrightarrow{\dot{n}}$	曲线上某点的单位法向量对时间的一阶导数
$k$	曲线上某点的曲率

而对于6个基础公式：

公式(1)、(2)描绘的是曲线点切向量、法向量对曲线弧长的导数关系

公式(3)、(4)描绘的是曲线点切向量、法向量对时间的导数关系

公式(5)、(6)描绘的是曲线点的位矢对时间的一阶导、二阶导关系

现在考虑一下两条曲线，一条曲线是车辆的轨迹线，一条曲线是参考线（即Frenet坐标系下的参考线）

所谓使用参考线作为坐标轴的意思就是：对轨迹上任意一点$t$，找到该点到参考线的投影点$b$，既然是投影点那么$t$点必然在$b$点的法向量方向上，考虑参考线上点$b$到参考线的起始点弧长为$s$，$t$在$b$的法向量方向上的距离为$l$，那么我们就把坐标($s$,$l$)称为以轨迹线为参考系的Frenet坐标。

为了方便推导笛卡尔坐标到Frenet坐标的转换公式，结合公式(1)、(2)、(3)、(4)、(5)、(6)，可以得到以下基础公式：

公式(7)~(13)分别描绘了轨迹点位矢对时间的一阶导(公式7)、参考线投影点位矢对时间的一阶导(公式8)、轨迹点切向量对时间的一阶导(公式9)、轨迹点法向量对时间的一阶导(公式10)、参考线投影点切向量对时间的一阶导(公式11)、参考线投影点法向量对时间的一阶导(公式12)、轨迹点加速度(公式13)

推导

经过预备知识的学习，问题就转化为了:

若已知笛卡尔坐标系下：

轨迹点的位矢、速度、加速度、曲率：$\overrightarrow{r_t}$、$\overrightarrow{v_t}$、$\overrightarrow{a_t}$、$k_t$

参考线的起点坐标：$(x_s,y_s)$

求Frenet坐标系下：

$s$，$\dot{s}$，$\ddot{s}$，$l$，$\frac{dl}{ds}(l^{'})$，$\frac{d^2l}{ds}(l^{''})$

1.求解第1步——计算投影点相关信息：

依据几何关系找到当前待计算轨迹点$t$在参考线上的投影点并计算(具体方法再写一篇)：

投影点的切向量和法向量：$\overrightarrow{\tau_b}$、$\overrightarrow{n_b}$ ，投影点的位矢、曲率、方向角：$\overrightarrow{r_b}=(x_b,y_b)$、$k_b$、$\theta_b$

根据简单的三角函数关系可得： $\overrightarrow{\tau_b}=(cos\theta_b,sin\theta_b)$、$\overrightarrow{n_b}=(-sin\theta_b,cos\theta_b)$

2.依据向量关系求解：

(1).求解$l$：

依据向量关系$\overrightarrow{r_t}=\overrightarrow{r_b}+l*\overrightarrow{n_b}$，两边同时乘$\overrightarrow{n_b}$可得：$l=\overrightarrow{n_b}(\overrightarrow{r_t}-\overrightarrow{r_b})$；

(2).求解$\dot{s}$：

(3).求解$\dot{l}$：

在(2)的推导中：两边同时乘$\overrightarrow{\tau_b}$的步骤改为两边同时乘$\overrightarrow{n_b}$直接得到：

(4).求解$l^{'} = \frac{dl}{ds}$：

(5).求解$\ddot{s}$：

这一步骤太麻烦了,先给个结论：

(6).求解$\ddot{l}$：

(7).求解$l^{''}=\frac{d^2l}{ds}$：

笛卡尔坐标转Frenet坐标公式总结

其中$t$为下标的量代表轨迹点(车辆点)相关的信息，$b$为下标的量代表投影点相关的信息。

想要完成笛卡尔坐标到自然坐标系的转换，不仅仅是套用计算公式就行，我们需要知道车辆的速度、加速度、位矢，投影点的曲率、切向量、法向量，那么如何得到这些信息呢，车辆轨迹点的信息应该是上游的定位模块给输出给我们，而匹配点信息需要依据高精地图给出的参考线(是离散点)信息进行计算，下一篇讲解投影点相关信息的计算。