图像特征 - 角点

一、harris角点检测

• 角点：将某点进行水平或垂直方向移动时，灰度级变化较大且迅速

  

1. 基本原理

① 推导过程

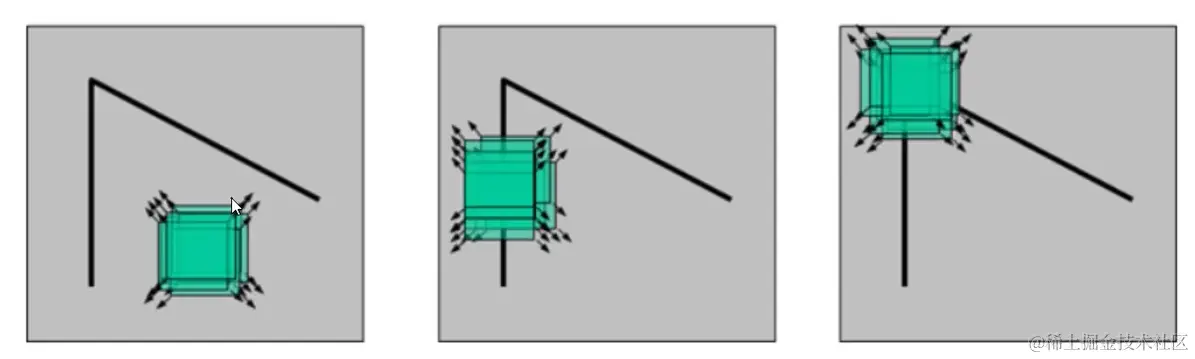
对于图像 l(x, y) ，当在点 (x, y) 处平移 $(\Delta x, \Delta y)$ 后的自相似性:

$c(x, y ; \Delta x, \Delta y)=\sum_{(u, v) \in W(x, y)} w(u, v)(I(u, v)-I(u+\Delta x, v+\Delta y))^{2}$

$w(\mathrm{x}, \mathrm{y})$ 是以点 $(\mathrm{x}, \mathrm{y})$ 为中心的窗口，既可是常数(盒状滤波器)，也可以是高斯加权函数：$\begin{bmatrix} 1 & 2 & 1\\ 2 & 4 & 2\\ 1 & 2 & 1 \end{bmatrix}$

可以基于泰勒展开对计算过程进行简化，也就是对图像I(x, y) 在进行平移($\Delta x, \Delta y$)后的结果进行一阶近似:

$I(u+\Delta x, v+\Delta y)=I(u, v)+I_{x}(u, v) \Delta x+I_{y}(u, v) \Delta y+O\left(\Delta x^{2}, \Delta y^{2}\right) \approx I(u, v)+I_{x}(u, v) \Delta x+I_{y}(u, v) \Delta y$

其中， $I_{x},I_{y} 是 I(x, y)$的偏导数

近似可得:

$c(x, y ; \Delta x, \Delta y) \approx \sum_{w}\left(I_{x}(u, v) \Delta x+I_{y}(u, v) \Delta y\right)^{2}=[\Delta x, \Delta y] M(x, y)\left[\begin{array}{l} \Delta x \\ \Delta y \end{array}\right]$

其中M:

$M(x, y)=\sum_{\omega}\left[\begin{array}{cc} I_{x}(x, y)^{2} & I_{x}(x, y) I_{y}(x, y) \\ I_{x}(x, y) I_{y}(x, y) & I_{y}(x, y)^{2} \end{array}\right]=\left[\begin{array}{ccc} \sum_{w} I_{x}(x, y)^{2} & \sum_{w} I_{x}(x, y) I_{y}(x, y) \\ \sum_{w} I_{x}(x, y) I_{y}(x, y) & \sum_{w} I_{y}(x, y)^{2} \end{array}\right]=\left[\begin{array}{ll} A & C \\ C & B \end{array}\right]$

化简可得:

$c(x, y ; \Delta x, \Delta y) \approx A \Delta x^{2}+2 C \Delta x \Delta y+B \Delta y^{2}$

$A=\sum_{w} I_{x}^{2}, B=\sum_{w} I_{y}^{2}, C=\sum_{w} I_{x} I_{y}$

上面的M矩阵为实对称矩阵，可以使用可逆矩阵进行相似对角化

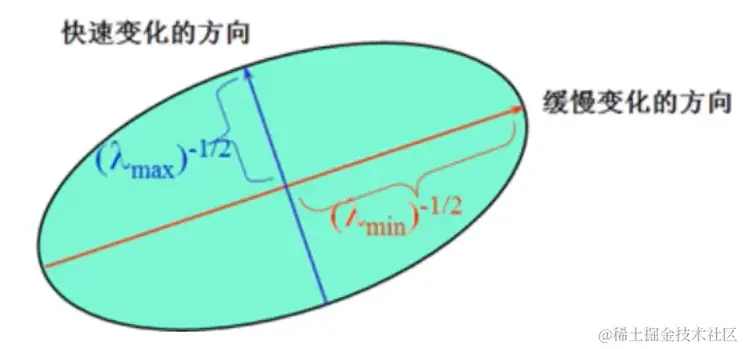
二次项系数本质上就是一个椭圆函数，椭圆方程为： $A \Delta x^{2}+2 C \Delta x \Delta y+B \Delta y^{2} = constant = [\Delta x, \Delta y] M(x, y)\left[\begin{array}{l} \Delta x \\ \Delta y \end{array}\right]$

但是这个椭圆并不标准，为了能使其标准化，则我们应该滤除C的干扰，所以我们应该对M矩阵进行相似对角化，最终M矩阵会化身为：$\left[\begin{array}{ll} \lambda_{min} & \\ & \lambda_{max} \end{array}\right]$,而椭圆方程也会转化为：$\lambda_{min} \Delta x ^{2} + \lambda_{max} \Delta y ^{2} = 1$

② 判别方法

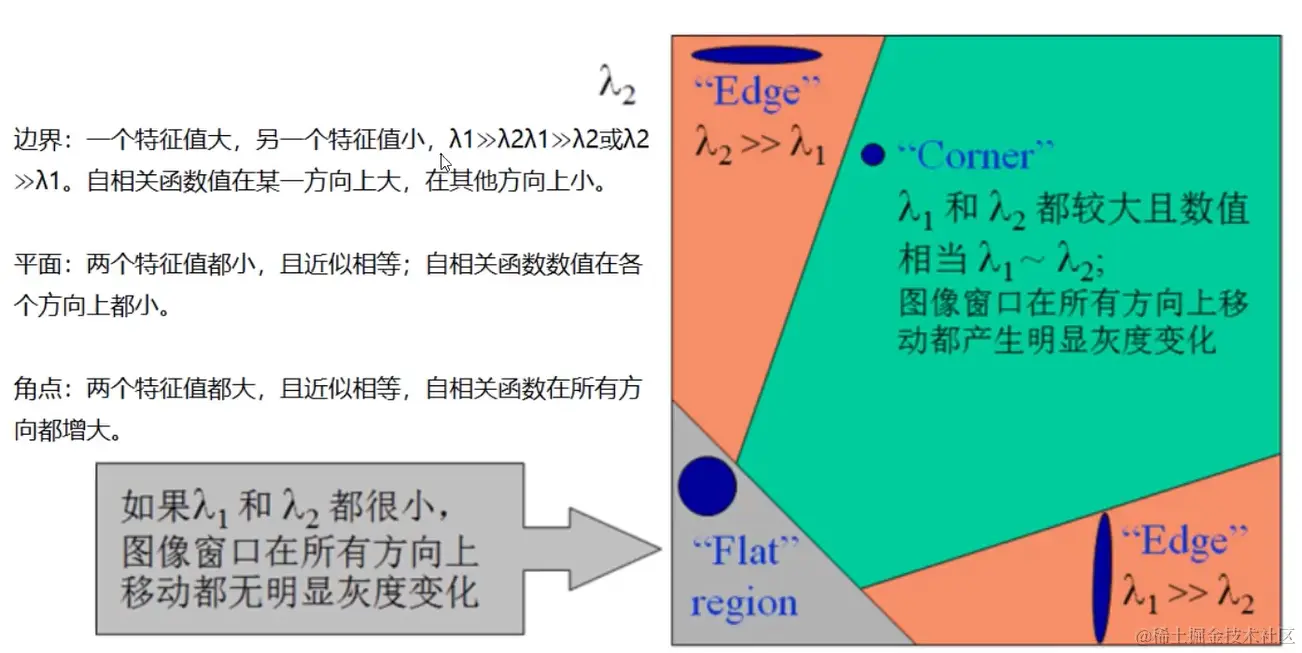
角点响应R值

• $R = detM - \alpha(traceM)^{2}$其中， $detM = \lambda_{1}\lambda_{2} 、 traceM = \lambda_{1} + \lambda_{2}$
• 判别方式：
  1. R > 0: 角点
  2. R < 0: 边界
  3. R = 0: 平坦

最后要使用NMS，非极大值抑制来进行最终遴选

二、工具包

cv2.cornerHarris()

• img:数据类型为float32的输入图像，最好是灰度图
• blockSize：角点检测中指定区域的大小
• ksize：Sobel算子中求导使用的窗口大小
• k：取值参数为[0.04, 0.06]，一般为0.04

import cv2
import numpy as np

%matplotlib inline

def cv_show(name,image):
    cv2.imshow(name,image)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

img = cv2.imread('chessboard.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

cv_show('Gray', gray)

cornerHarris函数的返回值只是计算出来的R结果，这个结果还需进行NMS

com = img.copy() # copy 是完全复制
res = cv2.cornerHarris(gray, 2, 3, 0.04)
# 直接根据 res 的结果对原图进行描点
img[res > 0.01 * res.max()] = [0,0,255] # ,用来分隔维度
res = np.hstack([com, img])
cv_show('Result', res)