正则化
一、过拟合问题
定义:在统计学中,过拟合(英语:overfitting,或称拟合过度)是指过于紧密或精确地匹配特定数据集,以致于无法良好地拟合其他数据或预测未来的观察结果的现象。
-
过拟合模型指的是相较有限的数据而言,参数过多或者结构过于复杂的统计模型。
-
发生过拟合时,模型的偏差小而方差大。过拟合的本质是训练算法从统计噪声中不自觉获取了信息并表达在了模型结构的参数当中。
-
相较用于训练的数据总量来说,一个模型只要结构足够复杂或参数足够多,就总是可以完美地适应数据的。过拟合一般可以视为违反奥卡姆剃刀原则。
1. 房价问题(线性回归)
-
各种假设函数
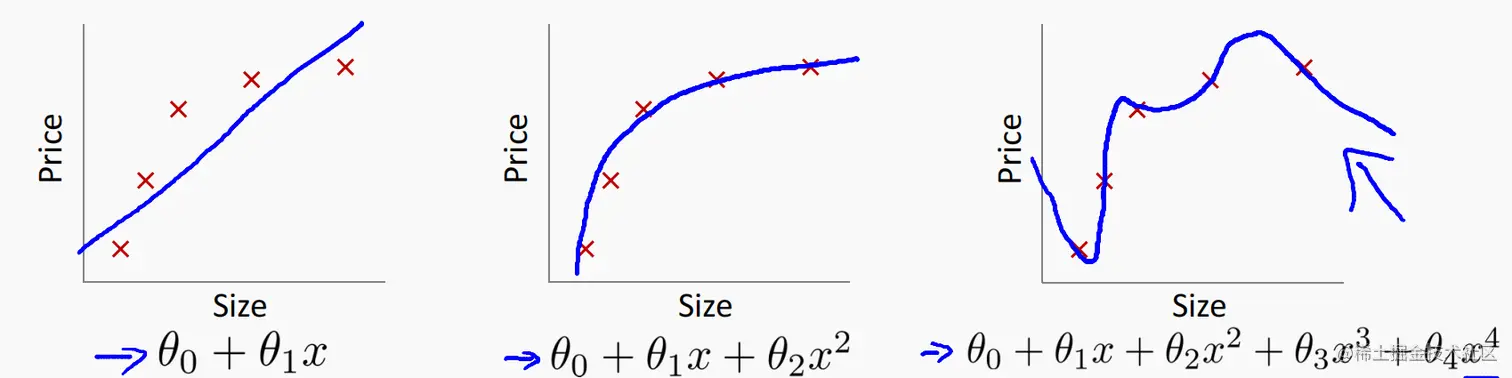
- 第一种直线拟合:预先认为问题是线性的。导致了欠拟合和高误差。
- 第二种适中:拟合效果较好。
- 第三种过拟合:太过依赖于输入样本的分布,不利于预测新样本的分布(没有普适性)
-
过拟合:
如果问题有太多的特征,那么假设函数就会过于追求贴合训练集(就是使代价函数最小化:J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2≈0),这也就导致了训练出来的模型不能推广至新样本(也就是不能准确的预测房价)
2. logistic 回归
-
各种决策边界
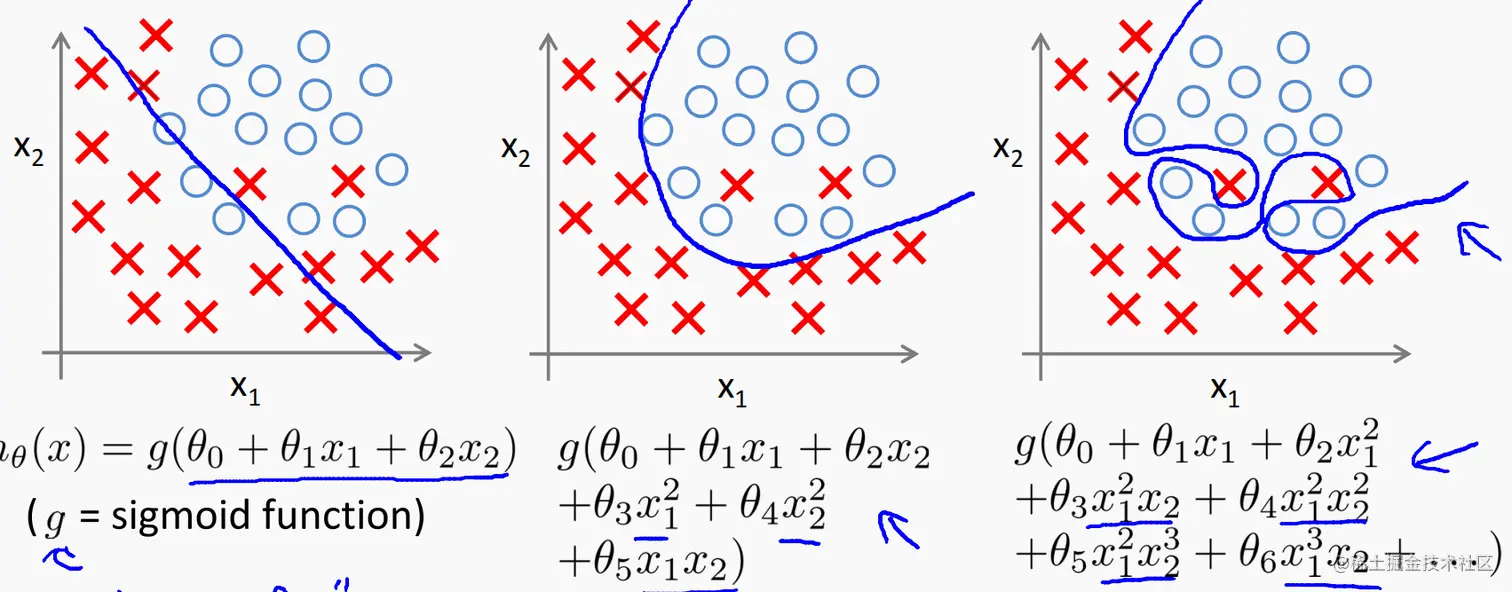
- 第一种情况:欠拟合
- 第二种情况:适中
- 第三种情况:过拟合
3. 解决办法
-
减少特征数量
- 手动选择应该留下的特征
- 利用模型选择特征的算法
-
正则化
二、代价函数
1. 过拟合的原因分析
-
示例
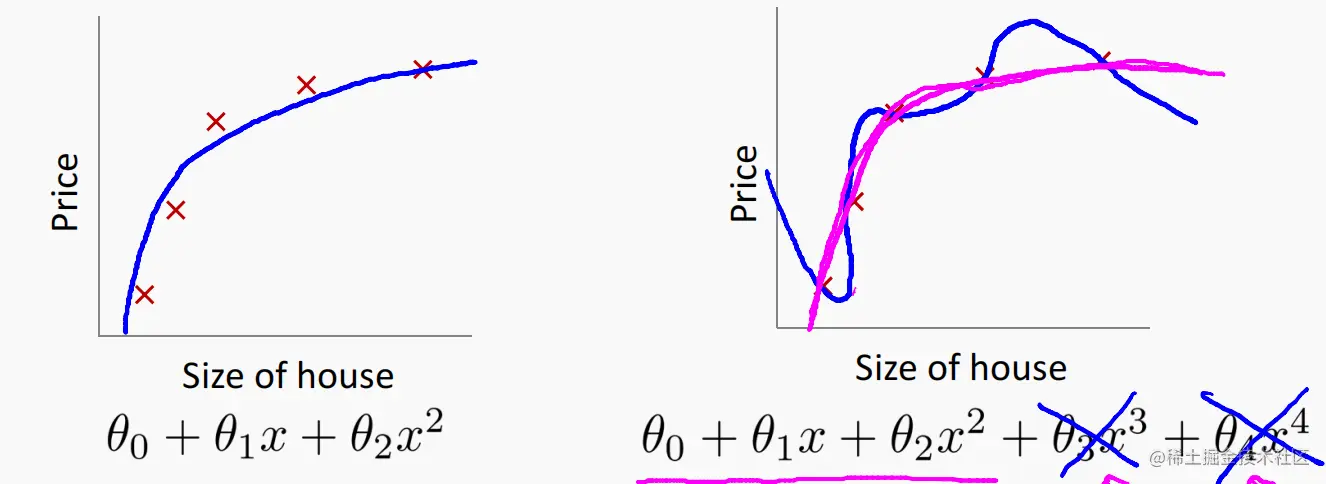
就是高量级的x过大,导致系数θj会更贴近输入的训练样本。
-
处理办法:
使高量级的x系数θj变小,也就是直接在代价函数后面加上高量级的两个系数,并在其前乘上一个正则化项:
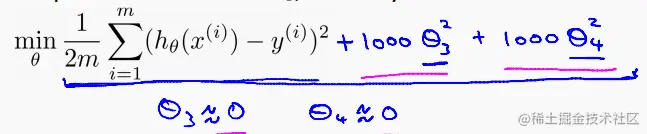 这样就能使最后的高量级系数变的很小,最终的假设函数就贴近低量级了。
这样就能使最后的高量级系数变的很小,最终的假设函数就贴近低量级了。
2. 正则化的作用
- 将较大量级 xn的系数θj变小,使整个模型贴近低量级
- 简化假设函数
- 减少过拟合的倾向
3. 房价示例
-
特征:x1、x2、x3、...、xn
-
参数:θ0、θ1、θ2、θ3、...、θn
- 注意:我们事先并不知道哪些系数是高量级的,所以我们要在代价函数后面添上对应的各个系数
-
代价函数
- J(θ)=2m1[∑i=1m(hθ(x(i))−y(i))2+λ(∑j=1nθj2)]
- 注意:若是正则系数λ设置过大,则会导致x的所有系数都达到一个非常小的值,此时对应的假设函数就相当于一个常数函数了,造成欠拟合。
-
若λ设置的非常非常大(例如为 1010),则会发生什么?
- 算法健壮性强,λ的大小不会影响整个流程
- 算法会陷入过拟合
- 算法最终欠拟合,最后甚至不能贴合训练集
- 梯度下降不收敛
三、线性回归中的正则化
1. 梯度下降
-
正则化代价函数
J(θ)=2m1[∑i=1m(hθ(x(i))−y(i))2+λ(∑j=1nθj2)]
-
流程
θ0:=θ0−αm1∑i=1m(hθ(x(i))−y(i))x0(i)θj:=θj−αm1[∑i=1m(hθ(x(i))−y(i))xj(i)+mλθj](j=1,2,3,…,n)
也可将下面的θj式子简化为:θj:=θj(1−αmλ)−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
-
一般会将正则系数λ设置得比较小,要使1−αmλ贴近0.99。
2. 正规方程
-
一般流程
-
不用使用繁琐求导来迭代θi,只要求出θ=(XTX)−1XTy就可以得出最佳结果。
-
推广:
-
m 个样本, n 个特征:m examples (x(1),y(1)),…,(x(m),y(m));n features.
x(i)=⎣⎡x0(i)x1(i)x2(i)⋮xn(i)⎦⎤∈Rn+1。x0(i)=1便于向量乘法。y=⎣⎡y(1)y(2)y(3)⋮y(m)⎦⎤∈Rm
-
加入正则化
X=⎣⎡(x(1))T⋮(x(m))T⎦⎤y=⎣⎡y(1)⋮y(m)⎦⎤
θ=⎝⎛xTx+λ⎣⎡011⎦⎤⎠⎞−1xTy,其中的矩阵是 n + 1 阶方阵,n 是特征个数。
-
若 λ > 0,则⎝⎛xTx+λ⎣⎡011⎦⎤⎠⎞一定可逆,所以正则化还解决了矩阵不可逆的问题。
四、逻辑回归中的正则化
-
存在问题:逻辑回归中也会出现过拟合
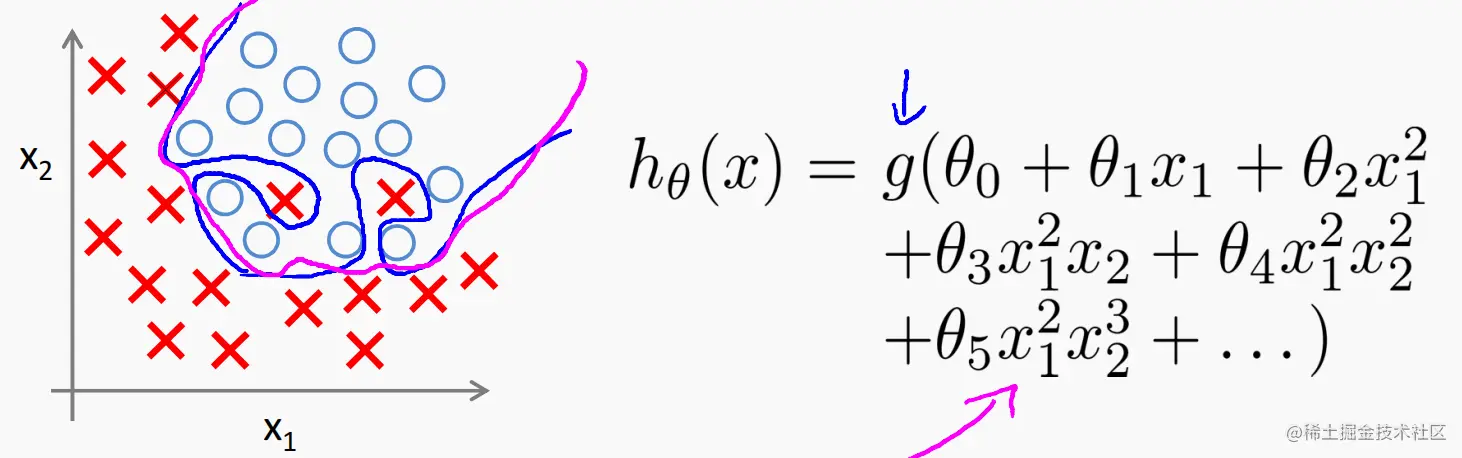
-
解决办法
-
在代价函数中加入"惩罚"
J(θ)=−[m1∑i=1my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))+2mλ∑j=1nθj2].
-
高级优化

这样就能使最后的高量级系数变的很小,最终的假设函数就贴近低量级了。