逻辑回归

一、矢量理解

好好利用Python的Numpy模块的线性代数库、数值线性代数库。

1. 样例

简化累加：
1. $\begin{aligned} h_{\theta}(x) &=\sum_{j=0}^{n} \theta_{j} x_{j} =\theta^{T} x \end{aligned}$ .本质就是行向量乘列向量会得到一个数而非矩阵。
2. Python语句如何表示？
简化梯度下降中的 ${\theta}$ 迭代：
1. $\theta_{j}:=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}$ ( for all j )
2. 计算过程：
  
  $\begin{aligned} \theta_{0} &:=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{0}^{(i)} \\ \theta_{1} &:=\theta_{1}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{1}^{(i)} \\ \theta_{2} &:=\theta_{2}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{2}^{(i)} \end{aligned}$
  
  第 i 个样例的输出只有 $y^{(i)}$ 一个，所以没有下标
3. 简化思想：[重点在向量和常数相乘]
  
  $\theta := \theta - \alpha \delta$
  
  其中， $\alpha$ 为学习率， $\delta = \frac{1}{m} \sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$ ，此处的 $x^{(i)}$ 是一个向量，内含第 i 行数据中的 n + 1 ( $x_{0} = 1$ )个特征：
  
  $x_{0}^{(i)},x_{1}^{(i)},x_{2}^{(i)}，......，x_{n}^{(i)}$ ，也即 $x^{(i)} = \begin{bmatrix} x_{0}^{(i)} \\ x_{1}^{(i)} \\ x_{2}^{(i)} \end{bmatrix}$ .
  
  所以可以得出 $\delta$ 也是一个向量， $\delta = \begin{bmatrix} \delta _{0} \\ \delta _{1} \\ \delta _{2} \end{bmatrix}$ , $\delta_{0} = \frac{1}{m} \sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}_{0}$

二、分类

概念：预测的值 y 是一个既定值(即预先知道结果是哪几种)。
例子：
1. 邮件分类:垃圾/正常
2. 线上交易：账户是否正常
3. 肿瘤：良性/恶性
一般 “坏” 就是阳性(positive), 也由 1 表示。

1. 分类中的线性回归

例子：肿瘤大小判断良性恶性
1. 设定阈值来判别，生成一元函数，通过 x 对 y 的映射值是否大于 0.5 来判别其是否为良性
2. 第一种情况
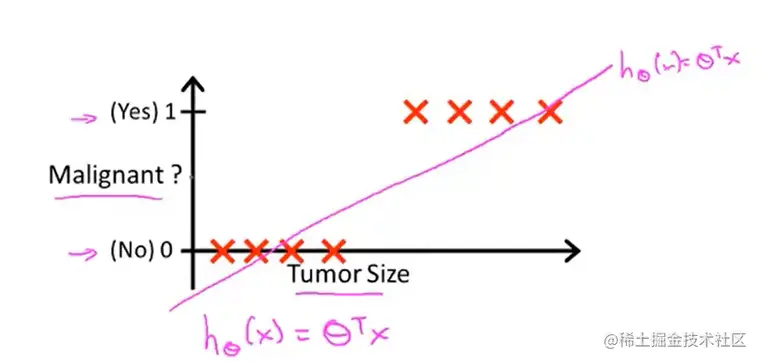
可以将此条线性直线的对应 y = 0.5 的 x 值作为阈值，当 x >= 0.5 ，则为 y = 1，阳 —— 恶性。
1. 第二种情况
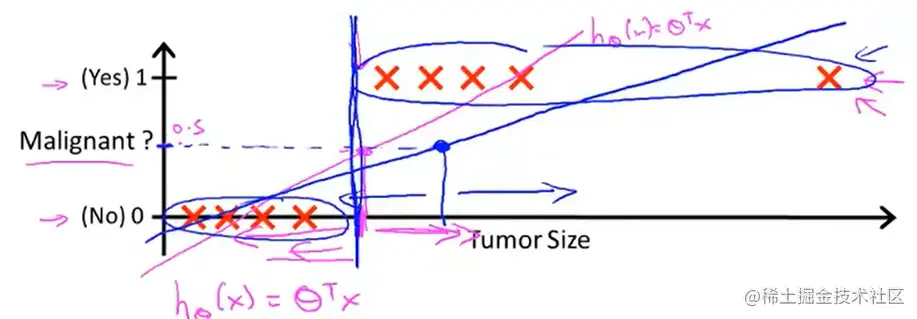
直线会因为一个噪声点而向平行于x轴的方向偏移，那么此时取 y = 0.5 对应的 x 只作为阈值的话，中间部分的点大部分都会判断为 y = 0，阴性，显然不正确。

可以看出线性回归并不适合于分类。而且如果映射出来的 y 非常大，而对应的范围有十分有限的时候，这种假设就没有必要。

2. 假设陈述

问题背景：

需要将 $h_{\theta}(x)$ 的值限定在 [0, 1] 范围内，需要另外一种假设函数(非线性)。

$h_{\theta}(x)$ = $g(\theta^Tx)$ ，也就是利用向量乘法简化计算。
Sigmoid函数：
1. g(z) = 1 / (1 + $e^{-z}$ )。
2. 图像如下：
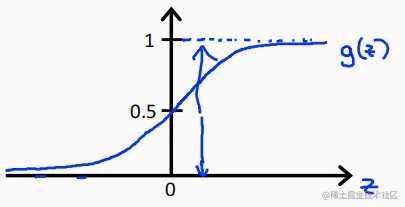
输出解释
1. 给出在输出为 x 的条件下，y = 1 的概率， $\theta$ 指的是模型的拟合数据。
  
  例如，若 $x = \begin{bmatrix} x _{0} \\ x _{1} \end{bmatrix}，h_{\theta}(x) = 0.7$ ，则表明当肿瘤尺寸为 $x_{1}$ 的情况下，其为恶性的概率为 0.7.后面会继续讨论二分类模型的输出，一般是将概率较大者作为结果输出。
2. 对于二分类问题：
  1. P( y = 0 | x, $\theta$ ) + P( y = 1 | x, $\theta$ ) = 1
  2. 移项可得：P( y = 0 | x, $\theta$ ) = 1 - P( y = 1 | x, $\theta$ )

3. 决策界限

什么时候将 y 预测为 0 或 1？
思想：直接使用概率代替输出。预测 y = 1 的概率大于等于 0.5 ，则输出 y = 1，否则 y = 0。而使 y = 1 的概率为 0.5 的这个 z = $\theta^Tx$ 取值就是决策边界。如下：

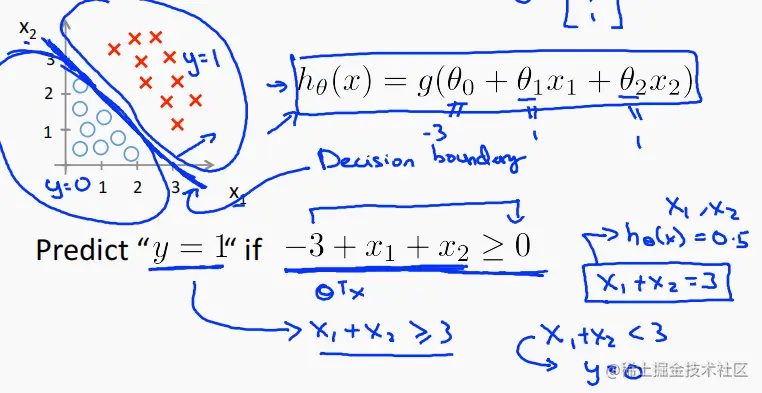
也就是由 g 值反推 x 的取值方式。就像上面说的，要取 y = 1作为输出，则取 y = 1 的概率要 P(y = 1 |x; $\theta$ )> = 0.5。从而将 g = 0.5 作为界限，而 g(z) = 1 / (1 + $e^{-z}$ )，当且仅当 z = $\theta^Tx$ = 0 时， g = 0.5。所以直接令 $\theta^Tx$ = 0 即可解出决策界限。
注意：决策边界是与数据集无关的，它只与假设函数有关。因为输入集中的 x 是不变的， $\theta$ 才是我们不断假设和解错的对象，也是假设函数得来源。
例子：[都是根据 ${\theta}$ 值进行绘制的]
1. 线性决策边界
  
  $h_{\theta}(x)=g\left(\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}\right)$ ，决策边界分析方式如上。
2. 环状(非线性)
  
  $h_{\theta}(x)=g\left(\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2} +\theta_{3} x_{1}^{2} + \theta_{4} x_{2}^{2}\right)$ ,决策边界的分析方式如上。

4. 代价函数

数据集

$\{ (x^{(1)}, y^{(1)}),(x^{(2)}, y^{(2)}),(x^{(3)}, y^{(3)}),......(x^{(m)}, y^{(m)})\}$ ，一共有 m 个样例，其中 x ∈ $x = \begin{bmatrix} x _{0} \\ x _{1} \\ x _{2} \\ ...\\ x _{n} \end{bmatrix}, x_{0} = 1, y 属于 \{0, 1\}$
假设函数

将 z = $\theta^{T} x$ 代入 g(z) = sigmoid(z) 中可得： $h_{\theta}(x) = \frac{1}{1+e^{-\theta^{T} x}}$
如何选择 ${\theta}$ ？
1. 代价函数： $J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \operatorname{Cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right)$
2. Cost 函数的一般映射：
  
  $\begin{array}{l}\\ \operatorname{Cost}\left(h_{\theta}(x), y\right)=\left\{\begin{array}{rr} -\log \left(h_{\theta}(x)\right) & \text { if } y=1 \\ -\log \left(1-h_{\theta}(x)\right) & \text { if } y=0 \end{array}\right. \end{array}$ ，可以从图像上来理解

三、模型优化

1. 简化代价函数和梯度下降

逻辑回归的一般代价函数：

$\begin{array}{l} J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \operatorname{Cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right) \\ \operatorname{Cost}\left(h_{\theta}(x), y\right)=\left\{\begin{array}{rr} -\log \left(h_{\theta}(x)\right) & \text { if } y=1 \\ -\log \left(1-h_{\theta}(x)\right) & \text { if } y=0 \end{array}\right. \end{array}$ ，此处的 y 的值只能为 0 或 1。
如何用一个式子来替换上面 Cost 分段函数？
1. 等式形式： $Cost\left(h_{0}(x), y\right)=-y \log \left(h_{0}(x)\right)-\left((1-y) \log _{y}\left(1-h_{\theta}(x)\right)\right.$ 。
2. 同理，利用 $(x_1 - a_1)(x_2 - a_2) ......(x_n - a_n) = 0$ 可以将任意段分段函数用一个式子表示。(当然此处的 x 一定要为整数)
3. 推广： $\begin{aligned} J(\theta) &=\frac{1}{m} \sum_{i=1}^{m} \operatorname{Cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right) \\ &=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right] \end{aligned}$
逻辑回归梯度下降

Gradient descent algorithm

$J(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]$

Want $\min _{\theta} J(\theta) :$

$Repeat \{\theta_{j}:=\theta_{j}-\alpha \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}$ .（利用整个数据集来同时更新所有 $\theta$ ）

同样应该使用矩阵 - 向量来简化计算
注意：

因为假设函数不同，所以线性回归和逻辑回归之间并没有关系。

逻辑回归也可以使用特征缩放来预处理数据

2. 高级优化

主要来探寻更适合于 logistic regression 的迭代方法，这些方法也应更适合于之后的庞大特征数据集。

梯度下降分析
1. 过程
  
  给定 $\theta$ 利用代价函数算出 J( $\theta$ )，利用偏导数来迭代 $\theta$ 。
2. 特点
  
  求导过程运算量大，收敛慢，但是算法简单。
另外的一些迭代算法
- Conjugate gradient
- BFGS
- L-BFGS
这些算法的一些优点：① 不用选择学习率 $\alpha$ ② 迭代时间通常比梯度下降要高；缺点就是比较复杂。
举例

3. 多元分类 —— 一对多

不同与之前的logistic regression 输出只有两个值，这里的多元分类要对应 3 个及以上。

引言
1. 应用举例：
  
  邮件标签：工作、朋友、家庭、爱好
  
  医疗诊断：健康、受凉、流感
  
  天气：晴朗、多云、雨天、下雪
处理思想：

将多元分类分为若干个二元分类的子问题(是或不是，类似于决策树)

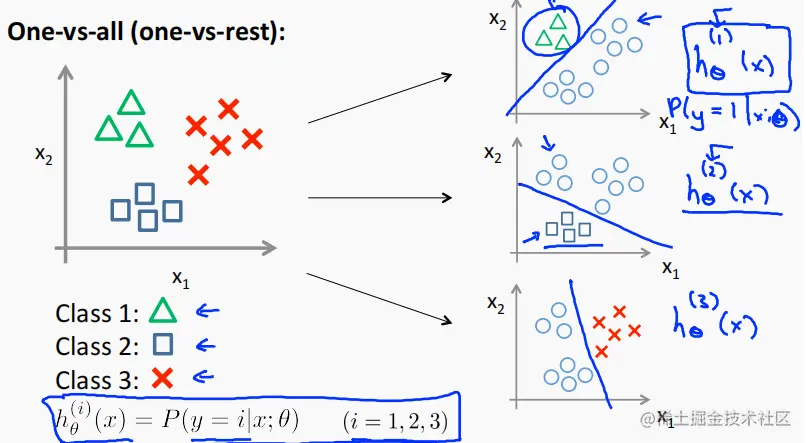
也就是对每一个特征进行 “是” 或 “不是”的假设，分别计算其概率。
处理步骤：
1. 训练一个逻辑回归分类器 $h_{\theta}^{(i)}(x)$ ，对每个 i 值分类进行 y = i的概率预测
2. 对输入值 x 使用该分类器得出结果，并将概率最大值 i 作为最终结果输出

ML 04 - Logistic Regression

逻辑回归

一、矢量理解

1. 样例

二、分类

1. 分类中的线性回归

2. 假设陈述

3. 决策界限

4. 代价函数

三、模型优化

1. 简化代价函数和梯度下降

2. 高级优化

3. 多元分类 —— 一对多