Linear Regression with multiple variables
多参数线性回归本质上是单参数线性回归的推广。
一、多功能
1. 前情回顾:
2. 多特征回归
-
数据集
| Size(feet^2) | Bedrooms number | Floors number | Home years | Price(feet^2) |
|---|
| x1 | x2 | x3 | x4 | y |
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
| 852 | 2 | 1 | 36 | 178 |
| …… | …… | …… | …… | …… |
-
样例术语
- n 代表特征数量,上表中 n = 4
- x(i)表示第 i 个训练样本。如 x(3) = ⎣⎡15343230⎦⎤,以列向量的形式给出。
- xj(i)表示第 i 个训练样本的第 j 个特征。如 x3(2) = 2
-
假设方程[多元方程]
hθ(x)=θ0x0+θ1x1+θ2x2+θ3x3+θ4x4+...+θnxn.
此方程中常把 x0取为 1 ,也就是将θ0作为常数项,便于之后利用矩阵乘法来简化计算 。
3. 利用向量简化计算流程
hθ(x)=θ0x0+θ1x1+θ2x2+θ3x3+θ4x4+...+θnxn.按照习惯,将未知量矩阵[向量] (θi)写在前面,已知量矩阵[向量] (xi)写在后面。以上面的房价预测为例:
[θ0θ1θ2θ3θ4]⎣⎡x0(1)x1(1)x2(1)x3(1)x4(1)x0(2)x1(2)x2(2)x3(2)x4(2)x0(3)x1(3)x2(3)x3(3)x4(3)x0(4)x1(4)x2(4)x3(4)x4(4)⎦⎤ = [y1y2y3y4]。式中的x0(i)一般取值都为1,如此一来,计算过程就十分简单了。
二、多元梯度下降法
1. 前情回顾[单特征回归]:
-
代价函数
J(θ0,θ1)=2m1∑i=1m(hθ(x(i))−y(i))2
-
迭代流程
Gradient descent algorithm
repeat until convergence {
θj:=θj−α∂θj∂J(θ0,θ1) (for j=0 and j=1 )
}
Correct: Simultaneous update(同步更新,学习率是一致的,且一定为正数)
temp0 :=θ0−α∂θ0∂J(θ0,θ1) temp1 :=θ1−α∂θ1∂J(θ0,θ1)θ0:= temp0 θ1:= temp1
-
偏导数
计算 j = 0 和 j = 1的对应的偏导数值:
∂θj∂J(θ0,θ1)=∂θj∂2m1∑i=1m(θ0+θ1x(i)−y(i))2j=0:∂θ1∂J(θ0,θ1)∂θ0∂J(θ0,θ1)=m1∑i=1m(hθ(x(i))−y(i))j=1:m1∑i=1m(hθ(x(i))−y(i))⋅x(i)
2. 多特征回归

3. 技巧
-
思路:确保所有特征都处于相似规模。
例如:x1∈ [1, 2000] (feet^2), x2∈ [1, 5] (number of bedrooms)。那么在进行迭代时,形成的等高线图就异常瘦长,造成迭代过程十分缓慢,降低效率。
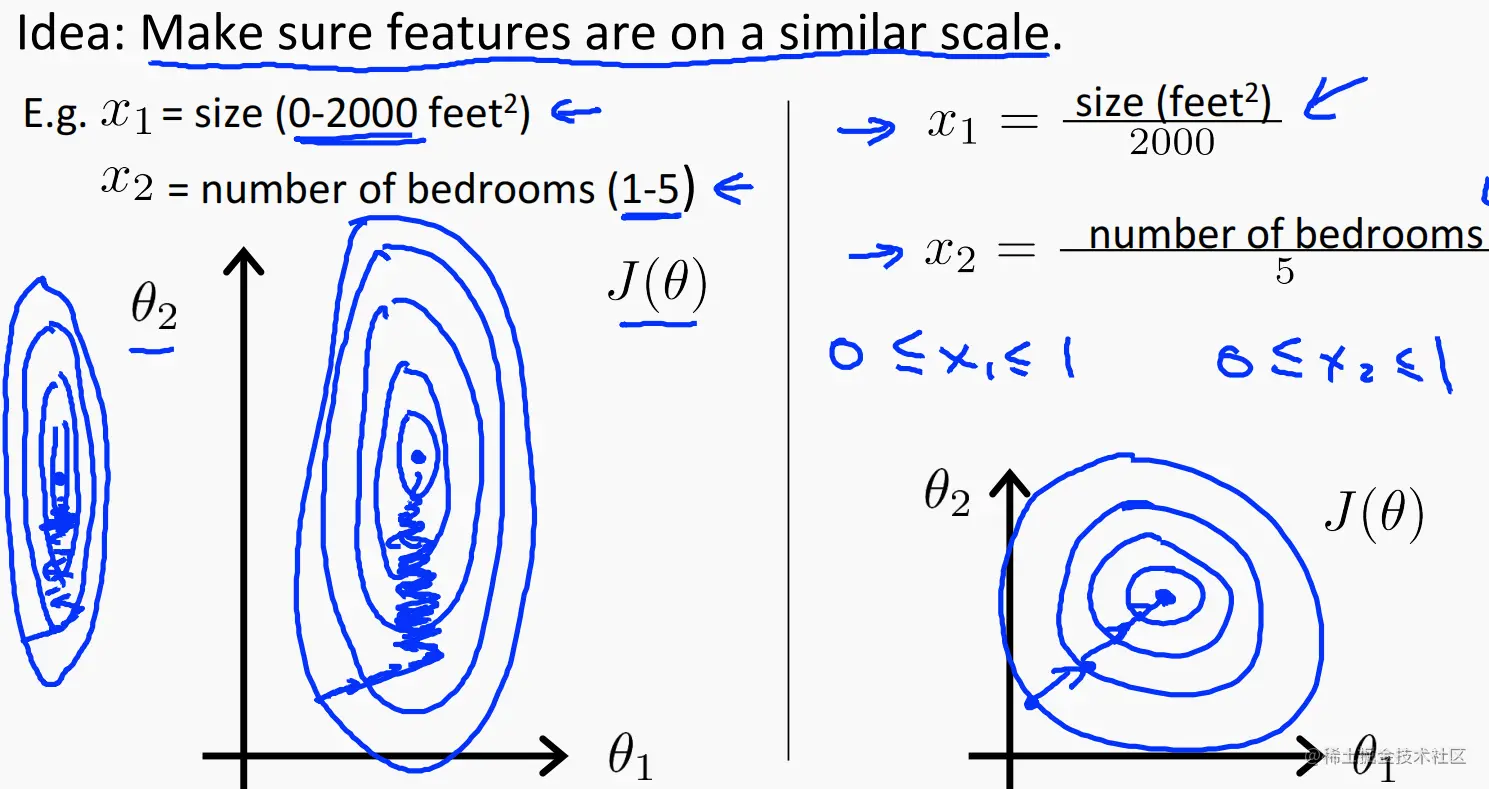
-
怎样进行?
可以直接将 对应的 xi除以区间长度进行缩放,俗称归一化。
上例中的 : x1 = size(feet^2) / 2000, x2 = number of bedrooms / 5。当然,xi也可以为负数。
-
另一种归一化:
x1=2000 size-1000 x2=5# bedrooms-2 −0.5≤x1≤0.5,−0.5≤x2≤0.5。xi的取值范围为 [- 0.5, 0.5]。
这样做的好处:使各参数迭代的更快,收敛所需的迭代次数更少。
-
学习率 α
-
迭代次数和代价函数 J 最小值的关系
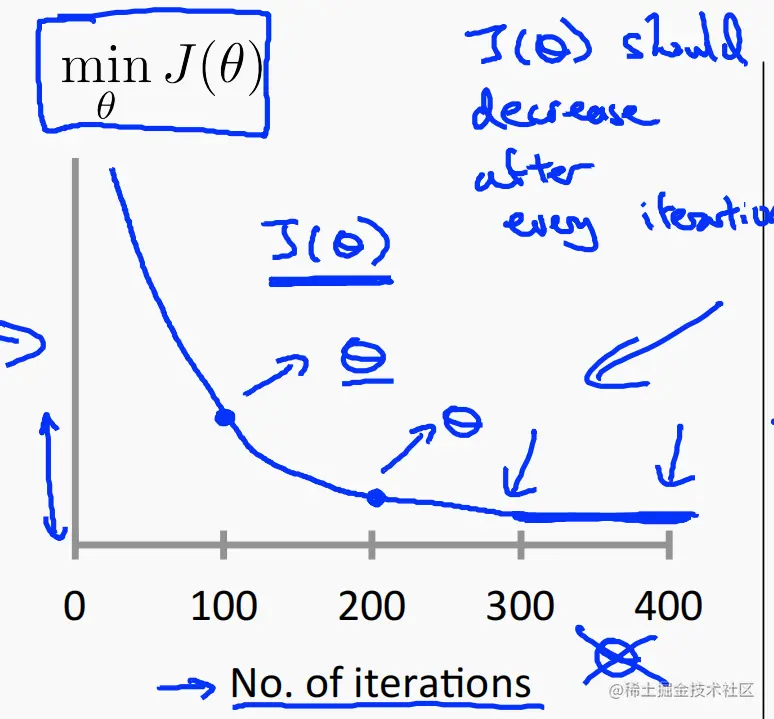
每次迭代都必须使 J 的最小值变小。若是在迭代过程中,代价函数 J 反而递增了,则应向下调整 α的值。
-
两种终止迭代的方法
- 模型自动进行收敛检测
- 声明 J 的最小阈值,到此为止
-
常见的α设置错误迭代方式
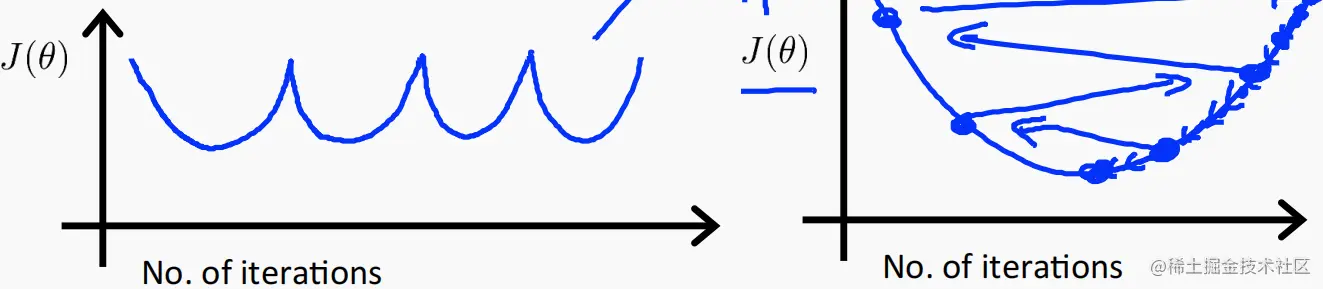
应向下调整 α的值。
4. 总结
α过大则可能导致 J 发散。α过小可能导致慢收敛(效率低)。
5. α的选取方法[* 3]
……,0.001,……, [0.003],……, 0.01,……, [0.03],……, 0.1,……, [0.3],……, 1,…….
三、特征和多项式回归
1. 特征简化
还是以上面的房价预测作为例子。
-
假设我们将房子的宽度(frontage)和纵深(depth)作为房子的两个特征,那么我们会得到如下的假设函数:
hθ(x)=θ0+θ1∗frontage+θ2∗depth.
-
我们可以适当简化各特征量,来简化迭代流程,如上面的 宽度(frontage)和纵深(depth) 就可以使用一个特征 :面积(Area = frontage * depth)来代替。
也即: hθ(x)=θ0+θ1∗Area.这样就会使迭代流程简化许多。
2. 选择假设函数
根据训练样本的基本分布图像来选择合适的假设函数。如下图:
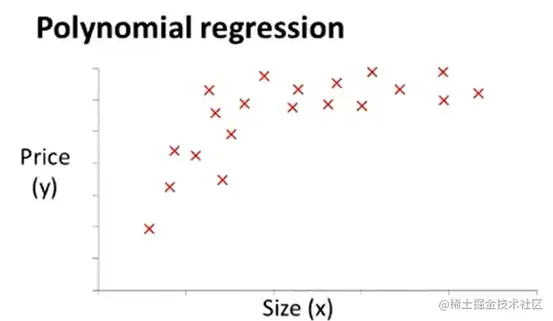
我们可以选择二次函数作为假设函数:hθ(x)=θ0+θ1∗x1+θ2∗x22,实际上 x1=x2。
但是这个二次函数只模拟了前面一段的 Size - Price关系,由于二次函数开口向下,则后面一定会出现随着 Size递增,Price反而递减的情况,所以不符题意。可作如下调整:
- 加入三次方:hθ(x)=θ0+θ1∗x1+θ2∗x22+θ3∗x33,当然此处的x1=x2=x2=Size。但是计算量又过大。
- 变为开二次方:hθ(x)=θ0+θ1∗x1+θ2∗x21/2——最佳选择。
四、正规方程
区别于之前的迭代方法的直接解法。之前的梯度下降法是一次性对所有θi进行迭代,而正规方程是逐步解决θi的取值。
-
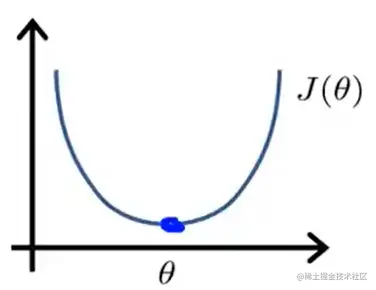
假设代价函数和θ的关系为:J(θ) = aθ2 + bθ + c,此处的θ为标量,如下图:
-
运用中学知识,要求J(θ)的最小值点,则应先对J(θ)求导,并将该式令为0,解出对应的θi。
-
梯度下降迭代θi的过程:
θ∈Rn+1J(θ0,θ1,…,θm)=2m1∑i=1m(hθ(x(i))−y(i))2∂θj∂J(θ)=⋯=0 (for every j)
Solve for θ0,θ1,…,θn,计算过程尤为繁琐,且此处的θ为一个向量。
-
改良:
-
例子: m = 4
| Size(feet^2) | Bedrooms number | Floors number | Home years | Price(feet^2) |
|---|
| x0 | x1 | x2 | x3 | x4 | y |
| 1 | 2104 | 5 | 1 | 45 | 460 |
| 1 | 1416 | 3 | 2 | 40 | 232 |
| 1 | 1534 | 3 | 2 | 30 | 315 |
| 1 | 852 | 2 | 1 | 36 | 178 |
| 1 | …… | …… | …… | …… | …… |
将数据集和对应的正确结果分别装入矩阵和向量。
X=⎣⎡11112104141615348525332122145403036⎦⎤y=⎣⎡460232315178⎦⎤。
-
重头戏:不用使用繁琐求导来迭代θi,只要求出θ=(XTX)−1XTy就可以得出最佳结果。
-
推广:
-
m 个样本, n 个特征:m examples (x(1),y(1)),…,(x(m),y(m));n features.
x(i)=⎣⎡x0(i)x1(i)x2(i)⋮xn(i)⎦⎤∈Rn+1。x0(i)=1便于向量乘法。y=⎣⎡y(1)y(2)y(3)⋮y(m)⎦⎤∈Rm.
-
正规方程和梯度下降的性能比较:
| Gradient Descent(梯度下降) | Normal Equation(正规方程) |
|---|
| 需要选择 α | 不用使用步幅α |
| 需要多次迭代 | 不用迭代,但是需要计算(XTX)−1 |
| 在 n (> = 10 ^ 6)较大的情况下,性能更佳 | 当 n 较小时,性能更好 |
- 矩阵不可逆的解决办法:
- 问题描述:使用正规方程解决θ的取值时,矩阵不可逆,即(XTX)−1非法。
- 产生原因:
- 特征冗余:x1 in feets2, x2 in m2,都表示房子面积
- 特征过多:可以删除某些特征或者使用正则化