线代基础
主要回顾一下矩阵和向量的有关知识。
一、矩阵
1. 定义
一个由数字组成的矩形数组。矩阵维数:行数 * 列数,如 Am∗n。
2. 矩阵元素表示方法
和计算机计数方式区别开来。Aij表示 A 矩阵中 第 i 行 , 第 j 列 的元素(从 1 ) 开始。
例如:A=⎣⎡123051⎦⎤,则 A12=0, A21=2。
-
注意
一般使用大写字母来表示矩阵,用希腊字母来表示向量
3. 矩阵加法
4. 矩阵乘法
-
乘以常数【也称为标量乘除】:
将此常数与所有矩阵元素相乘即可,除法自然同理3×⎣⎡123051⎦⎤=⎣⎡3690153⎦⎤[4603]/4=[11.500.75]
-
矩阵相乘:
两个矩阵能相乘的条件是:左矩阵的列数等于右矩阵的行数。
运算过程如下图:

例如:⎣⎡142301⎦⎤[15]=⎣⎡1647⎦⎤;[143021]⎣⎡105312⎦⎤=[1191014]; [1235][0312]=[915712].
-
矩阵和向量相乘:
运算过程如下图:
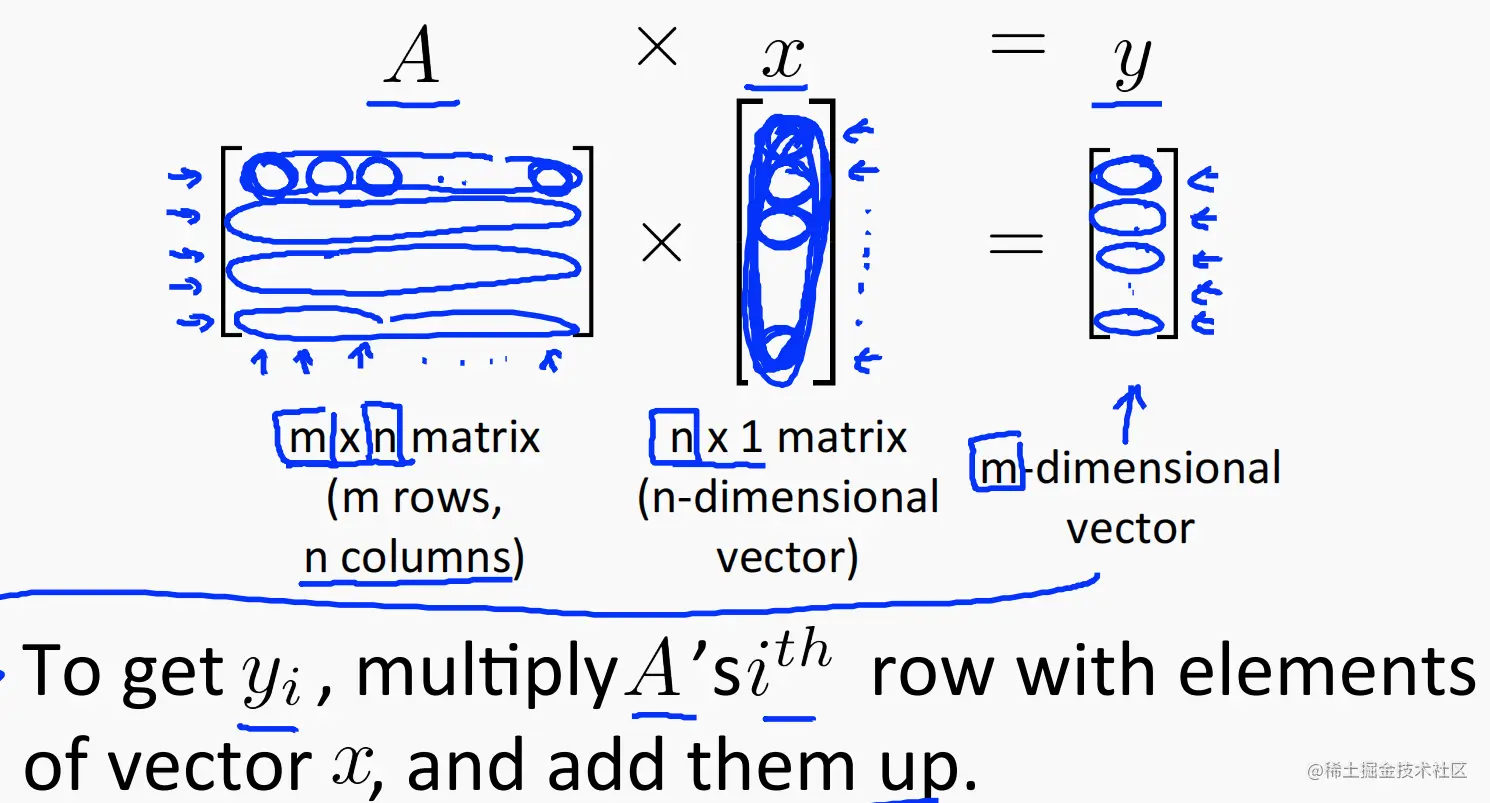
例如:⎣⎡10−123−2100540⎦⎤⎣⎡1321⎦⎤=⎣⎡1413−7⎦⎤
5. 矩阵乘法的特点
-
交换律:两个自然数进行乘法运算时,顺序不改变结果。但是两个矩阵相乘时,修改顺序可能得到不同结果。只有矩阵进行标量相乘【也就是乘以常数】才有交换律。
例如:[1235][0312]=[915712]. [0312][1235]=[27519].二者结果显然不同。
并且,假设 A - M * N, B - N * M,则 A B 所得结果是 M 阶方阵,而B A 的结果是 N 阶方阵。
-
结合律:矩阵乘法拥有结合律。即:A * B * C = (A * B) * C = A * (B * C)
-
单位矩阵:主对角线元素都是 1,其余元素全为 0 。有时会省略 0 。对于任意矩阵A,有: Em * A = A * En= A,其中 E 为 单位矩阵 。
6. 矩阵的逆和转置
A=⎣⎡10−123−2100540⎦⎤,则AT=⎣⎡12150304−1−200⎦⎤。 设 B = AT, 则 Bji=Aij 。
7. 应用
上一小结的线性回归预测房价:
-
四个房价和一个假设函数:
可以利用矩阵乘法来解决同时代入方程(避免使用循环):参数矩阵中的系数常数可以设置为 1
-
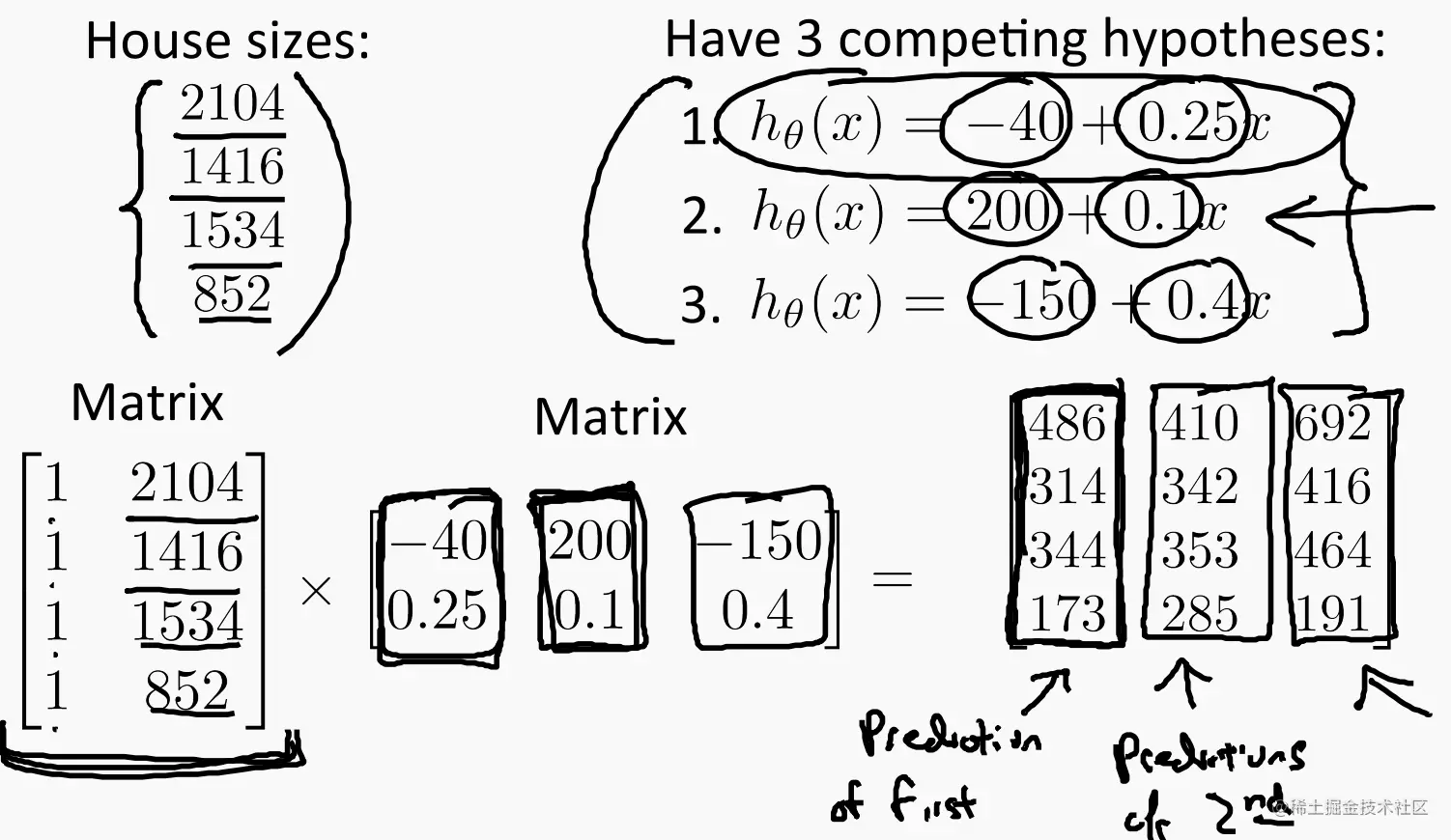
四个房价和三个假设函数:
将三个假设函数的θ0和θ1两个系数按横向拼接为系数矩阵,将样本参数纵向拼接为参数矩阵(常数项设为1),二者相乘得到结果。这样一次矩阵运算就进行了12次假设检验。
结果矩阵的列分别代表了不同假设函数对应的样本预测值。
二、向量
1. 定义:
一个 n * 1 或 1 * n 的矩阵
2. 向量元素表示法:
设 Y=⎣⎡1234⎦⎤,则yi表示第 i 个元素。如 y1=1, y2=2
3. 两种下标表示法:
- 1 起始:一般数学表示法。Y=⎣⎡y1y2y3y4⎦⎤
- 0 起始:计算机计数,便于计算机表示。Y=⎣⎡y0y1y2y3⎦⎤
4. 向量运算:
和矩阵运算规则是一致的:
3×⎣⎡142⎦⎤+⎣⎡005⎦⎤−⎣⎡302⎦⎤/3=⎣⎡21231/3⎦⎤