Non-photorealistic Radiance Remapping

Doi, K., & Morimoto, Y. (2020). Non-photorealistic Radiance Remapping. ACM SIGGRAPH 2020 Posters. doi:10.1145/3388770.3407395

本文提出了一种与强度 $I$ 相对应的颜色映射方法，该方法考虑到了光线在三维空间的物体之间的相互作用。而以往依据几何规范 (geometric specification) 或者渲染结果 (rendered result) 来映射颜色的方法，不能重现周围物体的相互反射。

利用路径追踪，用在采样的光线传播路径中的任意一维纹理，来代替出射 Radiance，最终出现在物体上的纹理是以修改后的估计值的加权平均值计算得出的，好处是可以根据物理强度产生颜色变化、再现焦散 (caustics) 或者色溢 (color bleeding) 等物理现象。

作者认为卡通着色所应用的

而通过路径追踪的方法，则可以将任意一维纹理应用于场景的视觉强度，以改变材料的外观。

在对所采样的光路行进每次评估时，根据路径使用带有权重的纹理，纹理坐标和权重都是根据强度 $I$ 计算的。

目的

由 PBR 渲染方程计算出出射 Radiance，即 $L_p$ 。再依据 $L_p$ 推导出其在出射方向 $\omega_o$ 的上对应的非真实感 Radiance，即 $L_{NP}$ 。

L_{P}=L_{e}+\int_{\mathcal{S}^{2}} f\left(\omega_{i}, \omega_{o}\right) L_{i}\left(\omega_{i}\right)\left|\mathbf{n} \cdot \omega_{i}\right| d \omega_{i}

为了解出 PBR 渲染方程，通常使用蒙特卡洛积分，以任意概率密度 $p$ ，对入射方向 $\omega_i$ 进行采样。

\hat{L}_{P}=L_{e}+\frac{f\left(\omega_{i}, \omega_{o}\right) L_{i}\left(\omega_{i}\right)\left|\mathbf{n} \cdot \omega_{i}\right|}{p\left(\omega_{i}\right)}

由 PBR 渲染方程得到的出射 Radiance $L_p$ 得出非真实感的出射 Radiance $L_{NP}$ 。

首先引入定义域为 $[0,1]$ 的一维纹理 $T(u)$ ，其中 $u$ 是从 $\hat{L}_{P}$ 映射得到的。

而 $L_{NP}$ 是通过对修改后的采样进行平均获得的，因此纹理值需要根据 $\hat{L}_{P}$ 对 $L_{NP}$ 的贡献，乘以 $W(\hat{L}_{P})$ 进行加权

\begin{aligned} L_{N P} &=\int_{\mathcal{S}^{2}} W\left(\hat{L}_{P}\right) T\left(u\left(\hat{L}_{P}\right)\right) d \omega_{i} \\ & \cong \frac{W\left(\hat{L}_{P}\right)}{p\left(\omega_{i}\right)} T\left(u\left(\hat{L}_{P}\right)\right) \end{aligned}

通过色调映射函数 Tonemap Function，依据出射 Randiance $\hat{L}_{P}$ 来映射强度 $I$

I=\text { tonemap }\left(\hat{L}_{P}\right)

具体来说就是强度 $I$ 通过将 $\hat{L}_p$ 转为 $X,Y,Z$ 颜色空间，并对 $Y$ 值进行伽马校正后获得 $I$ 。

将强度范围 $[I_{min},I_{max}]$ 归一化，定义为纹理坐标 $u$ ，以求出强度 $I$ 在一维纹理上的颜色值 $T(u)$ 。

u=\left\{\begin{array}{cc} 1 & \text { if } I_{\max } \leq I \\ \frac{I-I_{\min }}{I_{\max }-I_{\min }} & \text { if } I_{\min }<I<I_{\max } \\ 0 & \text { if } I \leq I_{\min } \end{array}\right.

权重函数 $W$ 由强度 $I$ 和出射 Randiance $\hat{L}_{P}$ 通过 $\alpha∈[0,1]$ 线性插值得到，但需要为强度 I 补充一个最小值 $w_{min}$ ，防止 $I$ 过小时变黑。

\frac{W\left(\hat{L}_{P}\right)}{p\left(\omega_{i}\right)}=(1-\alpha) \max \left\{I, w_{\min }\right\}+\alpha \hat{L}_{P}

本文使用该方法与

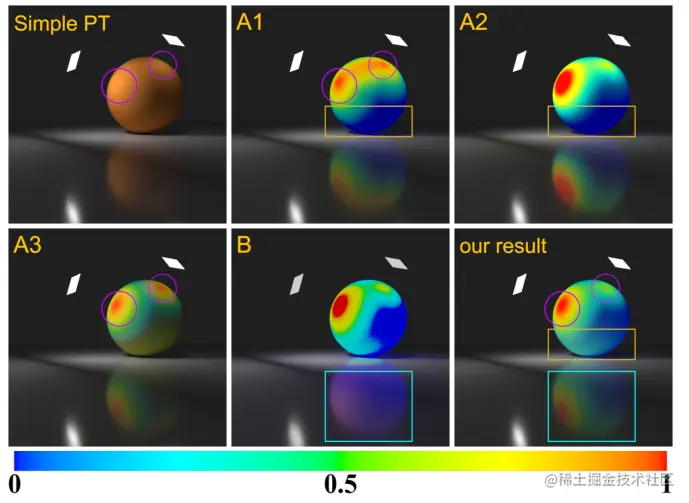
根据法线和入射方向之间的角度，来映射纹理，实现 $A1,A2,A3$

$A1$ ：通过计算 $u = \max \left\{n \cdot \omega_{i}, 0\right\}$ ，即法线和入射方向 $\omega_i$ 的余弦值，映射到一维纹理上得出。
$A2$ ：考虑了直接光照，计算直接漫反射部分 $D=f(\omega_i,\omega_o)L_i(\omega_i)(n,\omega_i)$ ，再依据法线和入射方向 $\omega_i$ 的余弦值，映射到一维纹理上。
$A3$ ：还考虑了间接光照，其中入射方向 $\omega_i$ 是沿着 BSDF 采样的，通过路径追踪的入射 Radiance 着色，依旧是依据法线和入射方向 $\omega_i$ 的余弦值，映射到一维纹理上。

$B$ 使用两个纹理输入，简单的路径追踪图像和包含球体的直接漫反射和简介反射的图像。使球体的渲染结果也是映射在一维纹理的范围内。