本文已参与「新人创作礼」活动，一起开启掘金创作之路。

深入理解OpenGL之投影矩阵推导

OpenGL流水线中的投影矩阵以及坐标变换

OpenGL中，投影矩阵在Vertex shader中使用，用于变换顶点。一般和Model, View矩阵结合成MVP矩阵后使用。Vertex shader的输出gl_Position是一个处于Clip Space中的齐次坐标。之所以叫做Clip Space，是因为OpenGL会在此空间中对图元进行裁剪（所谓图元就是三角形，线，点）。再这之后，进行透视除法，将通过clip的顶点从clip space的齐次坐标变换成一个3D坐标，这个坐标被称为归一化设备坐标(NDC: normalized device coordinates)。之所以叫归一化，因为这个坐标系的范围对于x,y,z都是从-1到+1，另外这个坐标系形成的几何体被称为规则观察体（CVV: canonical view volume)。再这之后，进行viewport transform将3D的NDC坐标转换成2D的屏幕坐标。

投影矩阵的作用，投影究竟是什么操作？

之所以在上面把经过投影之后的坐标的变换复习一遍，是因为我们需要从最终的目标出发理解投影矩阵的作用。因为如果仅仅从投影这个名词出发，是不能理解为何要变换到Clip Space再变换到NDC，然后最终变换到屏幕坐标。因为毕竟对于透视投影，将x,y坐标除以z就是从3D投影到2D，z越大，x和y越小，近大远小的效果就有了；而对于平行投影，直接将z值舍弃就完成了3D到2D的转换。OpenGL搞了那么多事情，都是为了最终能正确高效的进行渲染。 首先，在观察空间中，图元有可能在视景体内部也可能在外部，对于完全在外部的图元，没有必要进行渲染，所以需要丢弃这些图元，而完全在内部的图元需要保留；部分在内部的图元则需要进行剪裁，对于三角形，需要找出边和视景体边界的交点，将视景体内的部分生成一个或多个新的三角形图元，而在视景体外的顶点进行抛弃。但是直接在观察空间进行裁剪计算起来很麻烦，因为视景体形状和范围各不相同，需要比较复杂的计算才能完成裁剪。因此OpenGL将观察空间变换到规则观察体CVV，这样所有的坐标范围都是-1到+1，就比较容易计算了。需要指出的是，实际进行剪裁不是在CVV中，而是在裁剪空间(Clip Space)中。CVV中的NDC坐标范围是-1到+1，而Clip space中的x,y,z坐标满足$-W_c<=X_c<=W_c$, $-W_c<=Y_c<=W_c$, $-W_c<=Z_c<=W_c$，ClipSpace的齐次坐标经过透视除法将$X_c,Y_c,Z_c$都除以$W_c$就转换到了CVV中的NDC三维坐标。对于透视投影，我们将会看到，$W_c$的值是$-Z_e$，$(X_c,Y_c,Z_c)$除以$-Z_e$后得到了投影后的坐标，因此除以Wc被称为透视除法。 其次，对于投影来说，从3D转换到2D减少了一个维度，屏幕坐标只需要x,y值。但是为了进行深度测试以及裁剪，需要保留Z值。而且在后面的光栅化阶段，需要对顶点进行插值，得到中间的像素，除了对x,y插值，z也要插值。所以除了要保留Z值，还要保证插值后Z值的正确性。 再次，对于透视投影，还需要让生成的x,y坐标和z坐标成反比，以达到近大远小的效果。 所以，要完成以上这些目标，投影矩阵就需要多考虑一些事情，实际上有些图形学教材上例举的投影矩阵比OpenGL的简单一些，比如只是把x,y坐标按透视效果投影到投影面（OpenGL实际是投影到CVV），而投影前的z值没有保留；或者在此基础上保留了z值且插值后的z值是透视正确的，但是没转换到Clip Space，即对x,y坐标没有进行范围的映射。这些矩阵往往只是出于教学目的，OpenGL投影矩阵可以说是这些矩阵的超集。

小结一下，OpenGL坐标转换的过程： 【模型坐标 ----> [Vertex Shader] ---> 裁剪坐标 ---->[透视除法]---->NDC--->[Viewport变换]---->窗口坐标】 1-1）ModelView矩阵将模型顶点从模型坐标变换到View Space。 1-2）投影矩阵变换View space的顶点，得到的是Clip Space中的裁剪坐标（齐次坐标）。 2）在Clip Space中进行剪裁 3）进行透视除法，得到的是CVV中的NDC坐标 4）进行viewport变换，得到屏幕坐标。进行depthRange变换，得到定点数深度值。 5）光栅化阶段对顶点的屏幕坐标和深度值进行插值，得到图元所覆盖的像素（片段）的坐标和深度。 其中1-1,1-2在vertex shader中经常合并成MVP矩阵。而本文要讨论的投影矩阵就是将顶点从View space变换到Clip space。 展开一点讨论：上面的模型空间，视图空间，NDC都是3D坐标空间，尽管计算时顶点使用齐次坐标表示，但顶点的w值为1，直接提取x,y,z即得到3D坐标。而裁剪空间很特殊，其中的点也用齐次坐标表示，但w值通常不为1。(例如通过透视投影变换得到的裁剪空间坐标，w值为-Ze)。这样的一个裁剪空间不能简单的提取x,y,z得到一个对应的3D坐标空间，为了得到3D坐标，需要除以w，而除以w得到的就是NDC这个3D坐标空间。一般没法用图示表示裁剪空间，他真的不是一个立方体，因为它就不是3D空间。其实模型空间，视图空间从数学上说也是齐次坐标空间，因为你运算的时候使用的都是齐次坐标表示的顶点。只不过由于w为1，所以这些齐次点对应的3D点构成了3D空间的模型，视图空间。而裁剪空间也是一个齐次坐标空间，它对应的3D空间就是NDC，所以不精确的你也可以说裁剪空间是个立方体。

OpenGL的一些重要约定

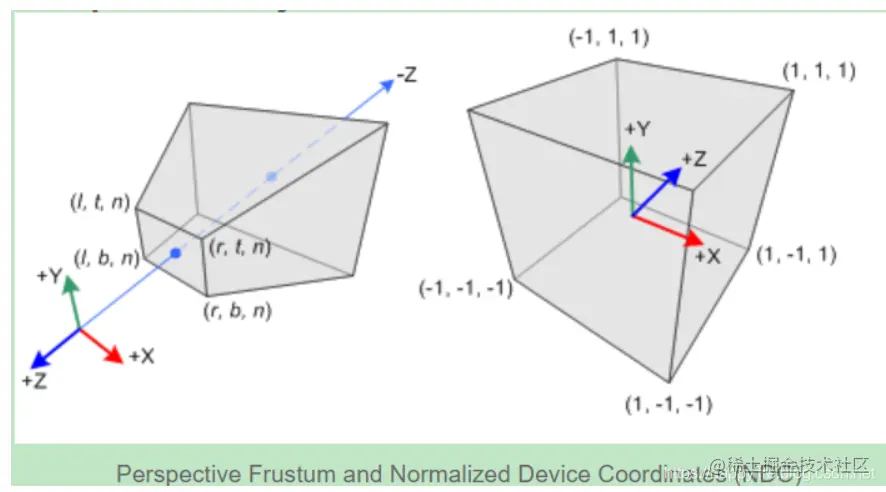
理解了投影究竟是干什么的，我们就可以开始推导投影矩阵了。但在这之前先让我们明确OpenGL的一些重要约定。 在投影之前，顶点处于View Space观察空间中，对于OpenGL，观察空间是+x向右，+y向上，+z向屏幕外的一个右手坐标系，观察方向沿着-z轴，即看向屏幕内部。也就是说如果我们没有模型和视图变换，vertex shader中指定顶点坐标默认使用的坐标系就是这样的一个右手坐标系。 通过投影（以及透视除法），顶点被变换到CVV中，在OpenGL中，CVV是一个坐标范围从$(-1,-1,-1)$到$(1,1,1)$的轴对齐立方体。而且重要的是，OpenGL的CVV是左手坐标系。这其实也好理解，因为OpenGL的视景体中，near plane被映射到NDC的$z=-1$平面，far plane被映射到$z=1$平面，而near pane离眼睛更近，因此NDC的+z轴就是指向屏幕内（+x, +y方向和观察空间相同），因此可以看出观察空间是右手坐标系，CVV(NDC)是左手坐标系。

两种投影矩阵

没错，我们要分别推导透视投影矩阵和平行投影矩阵。这两种投影使用的视景体的形状不同。对于透视投影采用frustum(平截头体），而平行投影采用一个轴对齐六面体。但是两种投影都是要变换（映射）到相同的CVV中。

推导OpenGL透视投影矩阵

目标：将视图坐标系中的顶点$P_e=(X_e,Y_e,Z_e)$变换到NDC坐标系中的顶点$Pn=(X_n,Y_n,Z_n)$，其中投影矩阵完成从$P_e$到裁剪空间顶点$P_c=(X_c,Y_c,Z_c,W_c)$的变换，然后$P_c$进行透视除法得到$P_n$。

结合上面的讨论，我们使用以下惯例和约定：

• 视图坐标系使用右手坐标系，NDC使用左手坐标系。NDC范围为$-1<= x <=1, -1<= y <=1, -1<= z <=1$
• 透视投影的视景体(frustum)由六个参数定义，对应了OpenGL的传统函数glFrustum(left, right, bottom, top, nearVal, farVal)。其中$left，right，bottom，top$为frustum的四个边平面在近视截面上所截出的矩形区域的$左边x=left，右边x=right，底边y=bottom和顶边y=top$。$nearVal和farVal$则为距离观察点的最近和最远距离，这两个是距离值必须为正（而由于观察空间中视线是看向负Z轴的，因此近远剪裁面的坐标为$z=-nearVal$和$z=-farVal$)。为了书写方便，下面这六个参数简写为$l，r，b，t，n，f$。
• NDC和屏幕的对应关系为：$x=1$的点在屏幕右边， $x=-1$在左边；$y=1$在顶部，$y=-1$在底部；$z=-1$的点距离观察者最近，$z=1$的点距离观察者最远。 约定很重要，因为约定不一样，推导出的矩阵不一样，比如n和f，OpenGL的约定为不含符号的正数距离值，而有些文章推导时n和f是包含符号的坐标值。再如OpenGL约定 $z=-n$ 映射到$z=-1$; $z=-f$映射到$z=1$，而有些图形学教材是将$n$映射到$z=1$, $f$映射到$z=-1$，这样矩阵的第三行符号就是反的。

推导过程

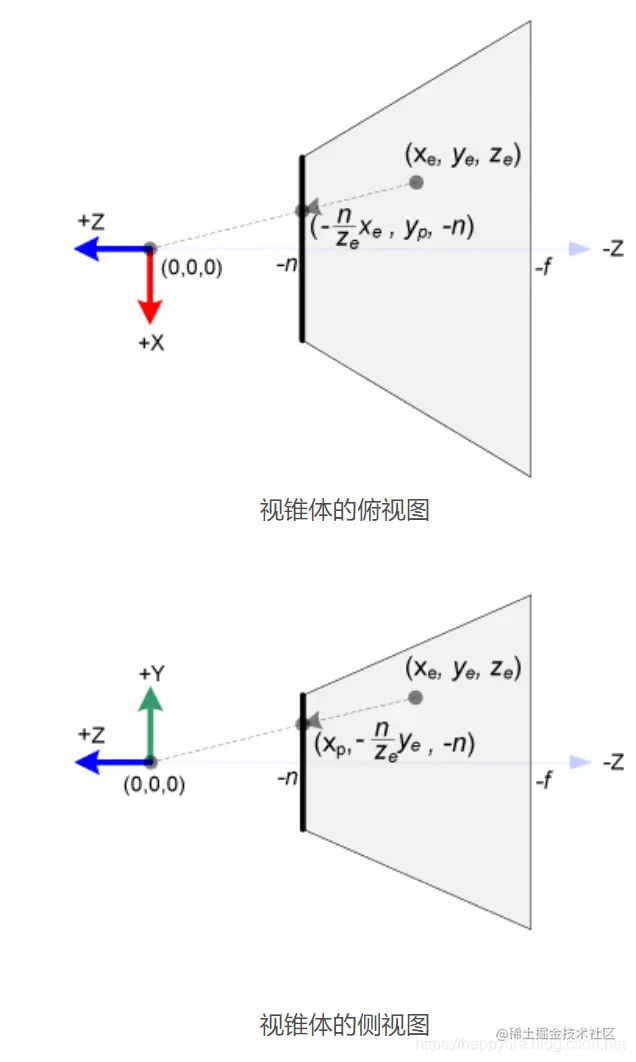首先，在视图空间中，我们以近裁剪面为投影面，计算视图空间中的一个点$(X_e,Y_e,Z_e)$在投影面上的坐标$(X_p,Y_p,Z_p)$，从俯视图可看出，根据相似三角形的比例关系： $\frac{X_p}{X_e} = \frac{Z_p}{Z_e}$，而$Z_p=-n$ 因此 $\frac{X_p}{X_e} = \frac{-n}{Z_e}$ $X_p = \frac{-nX_e}{Z_e}=\frac{nX_e}{-Z_e}$ 同样，根据侧视图，可计算得到 $Y_p = \frac{nY_e}{-Z_e}$ 即 $P_e=(X_e,Y_e,Z_e)$被投影到$P_p=( \frac{nX_e}{-Z_e}, \frac{nY_e}{-Z_e}, -n)$。注意投影后的z坐标总是$-n$，但是我们想在投影后仍然保留投影前z坐标的信息以便进行深度测试等工作。如果我们直接保留$Z_e$行不行呢？即$P_p=( \frac{nX_e}{-Z_e}, \frac{nY_e}{-Z_e}, Z_e)$。看上去没毛病，但是这是不行的。因为投影之后的光栅化阶段，需要在屏幕空间对顶点属性进行插值，以得到每个像素的深度值和其他属性如纹理坐标光照亮度等。而光栅化时在屏幕空间从点A到点B均匀的遍历像素，并根据像素到AB的距离对Z坐标进行线性插值，得到在屏幕空间均匀分布的Z值，可是每个像素逆投射回视图空间就会发现，这些像素在视图空间对应的Z值并不是均匀分布。具体请参考图形学基础之透视校正插值。实际上，光栅化时应该对Z坐标的倒数进行插值，因此需要建立关于1/Z的映射函数：$Z_p = \frac{A}{Z_e}+B$。综上所述，投影后得到的顶点为：

$P_p = (\frac{nX_e}{-Z_e}, \frac{nY_e}{-Z_e}, \frac{A}{Z_e}+B)$

而投影面上（近视截面）的顶点满足 $l \leq X_p \leq r$和 $b \leq Y_p \leq t$ 如上所说，视锥体通过投影矩阵（以及透视除法）最终变换为CVV，即$(X_p,Y_p,Z_p)$变换为NDC坐标$(X_n,Y_n,Z_n)$。而$X_n,Y_n,Z_n$的范围都是$[-1,1]$。首先我们处理x,y坐标，将$X_p,Y_p$映射到$X_n,Y_n$，即将$[l,n]$和$[b,t]$映射到$[-1,1]$的范围，这通过简单的线性函数就可以实现：

$X_n = \frac{2(Xp-l)}{r-l}-1$

$Y_n = \frac{2(Yp-b)}{t-b}-1$

代入上面关于$X_p,Y_p$的表达式：

$X_n = \frac{2(\frac{nX_e}{-Z_e}-l)}{r-l}-1 = \frac{2n}{r-l}(\frac{X_e}{-Z_e})-\frac{2l}{r-l}-1$

$X_n = \frac{2n}{r-l}(\frac{X_e}{-Z_e})-\frac{r+l}{r-l}$

同样可得

$Y_n=\frac{2n}{t-b}(\frac{Y_e}{-Z_e})-\frac{t+b}{t-b}$

这就得到了从视图坐标的xy到NDC坐标的xy的映射关系，下面找一下z坐标的映射关系$Z_n=f(Z_e)$，即视图空间Z坐标和NDC的Z坐标的函数。 由于我们将视图空间投影后的z坐标设置为$\frac{A}{Z_e}+B$的形式，而从投影坐标到NDC坐标是线性映射，因此可将NDC坐标$Z_n$也记为$\frac{A}{Z_e}+B$，只是相对于$Z_p$其A,B值不同。 已知视图空间z坐标$Z_e$的范围是$[-f,-n]$，对应了NDC中的z坐标范围$[-1,1]$，且$-n$映射到$-1$，$-f$映射到$1$，因此将$-n,-f$分别代入$Zn=\frac{A}{Ze}+B$得：

$-1 = \frac{A}{-n}+B$

$1 = \frac{A}{-f}+B$

可解出A,B为：

$A=\frac{2nf}{f-n}$

$B=\frac{f+n}{f-n}$

将A,B代入$Zn=\frac{A}{Ze}+B$的表达式后，即可得到$Z_e和Z_n$的关系式：

$Z_n=\frac{\frac{2nf}{f-n}}{Ze}+\frac{f+n}{f-n}$，即：

$Z_n = \frac{-2nf}{f-n}(\frac{1}{-Z_e})+\frac{f+n}{f-n}$

至此，我们已经得到了视图空间坐标$(X_e,Y_e,Z_e)$到NDC坐标$(Z_n,Y_n,Z_n)$的函数：

$X_n = \frac{2n}{r-l}(\frac{X_e}{-Z_e})-\frac{r+l}{r-l}$

$Y_n=\frac{2n}{t-b}(\frac{Y_e}{-Z_e})-\frac{t+b}{t-b}$

$Z_n = \frac{-2nf}{f-n}(\frac{1}{-Z_e})+\frac{f+n}{f-n}$

上文说过，从视图坐标到NDC坐标的变换分为两个过程，即先通过投影矩阵变换得到裁剪空间的齐次坐标，然后经过透视除法得到NDC坐标。我们已经得到了NDC坐标$(X_n,Y_n,Z_n)$，为了得到投影矩阵，需要得到裁剪空间的齐次坐标$(X_c,Y_c,Z_c,W_c)$。由于$X_n = \frac{X_c}{W_c}$, $Y_n = \frac{Y_c}{W_c}$, $Z_n = \frac{Z_c}{W_c}$,且上面的$X_n,Y_n,Z_n$的表达式中，都有$-\frac{1}{Z_e}$，显然可以令$W_c=-Z_e$，$X_n,Y_n,Z_n$分别乘以$-Z_e$得到$(X_c,Y_c,Z_c,W_c)$为：

$X_c = \frac{2n}{r-l}X_e+\frac{r+l}{r-l}Z_e$

$Y_c=\frac{2n}{t-b}Y_e+\frac{t+b}{t-b}Z_e$

$Z_c = -\frac{f+n}{f-n}Z_e-\frac{2nf}{f-n}$

$W_c=-Z_e$

以上都是关于$P_e=(X_e,Y_e,Z_e)$的线性函数，可以用矩阵表示为：

即得到了OpenGL的透视投影矩阵

关于Z值插值的一点补充

上文说到，为了对$\frac{1}{Z_e}$进行插值，我们将$Z_n$定义成$\frac{A}{Z_e}+B$的形式，然后在光栅化时经过glDepthRange的映射，将$[-1,1]$的$Z_n$映射为$[0,1]$的Z值，这个Z值被写到Z Buffer中。按理说插值Z应该就是用这个将写入Z Buffer的Z值了。但是我在某本书上看到，使用clip space的W值的倒数进行插值。clip space顶点是vertex shader的输出，其顶点的W值就是$-Z_e$，因此感觉也是挺科学的。具体什么情况，等我弄清楚了再补充。

gluPerspective风格的透视投影矩阵

OpenGL固定流水线的传统函数

void gluPerspective(	GLdouble fovy,
 	GLdouble aspect,
 	GLdouble zNear,
 	GLdouble zFar);

这其实是另外一种定义frustum视截体的方式，不同的是这种方式定义的视截体的中心在Z轴，也就是说，glFrustum矩阵中当$l=-r, b=-t$时的情况。 fovy为视截体在yz平面上的夹角，aspect为裁剪面的宽高比。因为左右上下对称，因此可知对于glFrustum矩阵中的$l,r,b,t$,$l,b$为负值，$r,t$为正值，因此可计算得到：

$tan(fovy/2) = \frac{t}{n}$

$t = n*tan(fovy/2)$

$b=-t = -n*tan(fovy/2)$

$r = aspect * t = n*aspect*tan(fovy/2)$

$l = -r = -n*aspect*tan(fovy/2)$

将$l,r,b,t$代入上面的glFrustum矩阵中，可得gluPerspective矩阵：

推导OpenGL平行投影矩阵

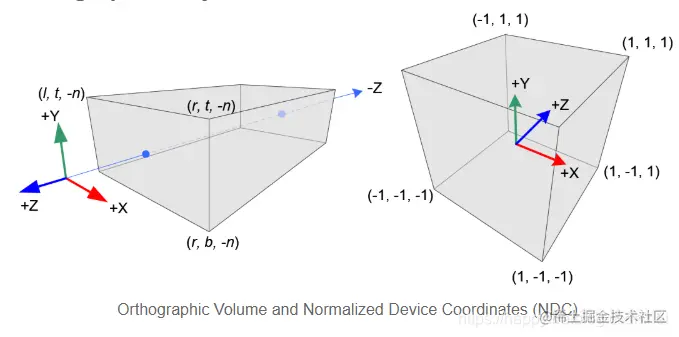如图所示，平行投影的视景体是一个轴对齐六面体，由于没有透视效果，我们只需要将视景体映射到NDC。

目标：将平行投影视图坐标系中的顶点$P_e=(X_e,Y_e,Z_e)$变换到NDC坐标系中的顶点$P_n=(X_n,Y_n,Z_n)$。

约定：

NDC的约定同透视投影，视景体的定义同传统OpenGL函数$glOrtho(left, right, top, bottom. near, far)$。前4个参数分别定义了视景体的左右上下四个面。near, far是近裁剪面和远裁剪面相对于视点的距离，但是和透视投影不同，near, far不一定是正数。如果near或far小于0，则表示位于视点后面（视点位于$(0,0,0)$）。同样为了书写方便，这六个参数简写为$l, r, t, b, n, f$。这样$(r,t,-n)$表示的是近裁剪面的右上角。

推导过程

如上所述，由于平行投影的视景体是一个轴对称六面体，而NDC是一个立方体，也是轴对称的。因此只需要简单的线性映射，即可将视景体中的顶点$P_e=(X_e,Y_e,Z_e)$变换到NDC中的顶点$P_n=(X_n,Y_n,Z_n)$。这只需要先将六面体的长宽高缩放到2，然后将中心点移动到立方体中心即可。 以X坐标为例，我们需要将$X_e$映射到$X_n$，其实这和上面透视投影将$X_p$映射到$X_n$是一样的，但是之前没有具体推导，一笔带过了。这儿稍微详细推导一下： 由于$X_e$的范围是$[l,r]$，$X_n$的范围是$[-1,1]$，因此通过 $\frac{1-(-1)}{r-l}.X_e$即可把$X_e$缩放到$[-1,1]$，然后再进行一个偏移将中心点移动到原点，假设偏移量为$B$,则可得：

$X_n = \frac{1-(-1)}{r-l}X_e+B$

为了计算出$B$，我们将$X_e=r和X_n=1$带入上式

$1 = \frac{2}{r-l}r+B$，可得

$B=-\frac{r+l}{r-l}$，将其代入上式，可得：

$X_n = \frac{2}{r-l}X_e-\frac{r+l}{r-l}$

同样可得

$Y_n = \frac{2}{t-b}Y_e-\frac{t+b}{t-b}$

$Z_n$的推导过程一样，只是由于$n,f$是距离值，因此其坐标表示为$-n,-f$，不失一般性在上图所示的情况下, $-f映射到1，-n映射到-1$，因此:

$Z_n = \frac{1-(-1)}{-f-(-n)}Z_e+B$

代人$Z_n=1, Z_e=-f$

$1 = \frac{2}{n-f}(-f)+B$,得

$B = \frac{2f}{n-f}+1=\frac{n+f}{n-f}$,因此：

$Z_n = \frac{2}{n-f}Z_e+\frac{n+f}{n-f}$

$Z_n = \frac{-2}{f-n}Z_e-\frac{f+n}{f-n}$

由此，我们得到了$P_e$到$P_n$的线性映射关系，我们实际需要的是$P_e$到$P_c$的线性关系，因为投影矩阵变换后得到的是Clip Space的顶点。但对于平行投影，w值没有意义，因此可以任意指定，这样我们指定w=1，即可直接将$P_c$用$P_n$表示，最终我们得到如下表达式：

$X_c = \frac{2}{r-l}X_e-\frac{r+l}{r-l}$

$Y_c= \frac{2}{t-b}Y_e-\frac{t+b}{t-b}$

$Z_c = \frac{-2}{f-n}Z_e-\frac{f+n}{f-n}$

$W_c= 1$

以上都是关于$P_e=(X_e,Y_e,Z_e)$的线性函数，可以用矩阵表示为：

即得到了OpenGL的平行投影矩阵

补充

最近学习了GAMES101课程，闫令琪老师讲解了图形学约定下投影矩阵的推导，非常值得一看： www.bilibili.com/video/BV1X7… 其中的约定和OpenGL稍微有些不同，一是OpenGL中NDC空间是左手坐标系，而闫老师推导的是右手坐标系，即和视图坐标系一致。二是关于n和f，OpenGL是距离值，而闫老师使用的是坐标值。 推导的过程非常好，比如平行投影矩阵，只是先将frustum平移到原点，然后坐一个缩放，直接将两个矩阵相乘就得到投影矩阵。由于约定的不同，在闫老师的矩阵中将n和f取反，并且将z乘以-1，最终得到的矩阵和OpenGL就是一样的了。