本文内容皆引用于知乎用户 Monica的小甜甜

• 【论文复现】The Power of Box Filters - 知乎 (zhihu.com)

The Power of Box Filters: Real-time Approximation to Large Convolution Kernel by Box-filtered Image Pyramid

SIGGRAPH Asia 2019 Technical Briefs

介绍

在空间范围内进行滤波本质是对一个着色点与他周围着色点进行一些处理，最关键的就是如何获取该着色点周围着色点的信息。和传统的高斯滤波直接对周围点进行采样不同，本文提出了一个新方法，即从 $mipmap$ 里获取周围点信息用于滤波，显然采样率就大大减少了。

例如，对于一个 $1024\times1024$ 分辨率的纹理进行采样，$mipmap$ 的层级仅有 $10$ 级，即需要 $10$ 次采样。而 $mipmap$ 的生成可以直接通过硬件加速生成：在一些图形 API 中，图形驱动程序已经实现了盒型滤波器的 $mipmap$ 生成，并做了专门的优化，因此盒型滤波器的实现成本很低。

方法

采样公式

高斯滤波采样公式

对于一个着色点 $x$ 想要进行高斯滤波，首先要取该着色点周围 $R\times R$ 方形区域里面的像素然后在乘以高斯滤波函数。

$G(x,y)$ ：二维的高斯滤波函数。由于高斯滤波有个很好的特性：可以先在 $x$ 方向进行滤波，然后再在 $y$ 方向滤波。因此实际过程中通常用于一维的高斯滤波函数。

$t(x,y)$ ：对着色点进行采样的函数。采样时只是单纯的后处理，即对一张纹理进行处理，因此没有z方向。

盒型滤波采样公式

$p_{down} (L)$ ：着色点 $x$ 在第 $L$ 层（当前层）的 $mipmap$ 纹理颜色，该纹理采样是对等待滤波的纹理进行采样。

$w(L)$ ：盒型滤波的权重，该值是根据高斯滤波所推导得出，在后面介绍如何推导。

$m$ ：$mipmap$ 的最大层数理论上为无穷大。

论文中对上述公式进行了变形，给出了递归求法：

$p(x,L)$：着色点 $x$ 在第 $L$ 层的纹理颜色。

$\alpha(L)$ ：每层采样过程的混合权重 。

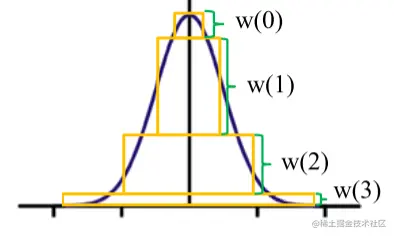
权重推导

对于一个着色点 $p$ ，对其应用盒型滤波的结果应该与高斯滤波是相同的。但对于盒型滤波，由于 $mipmap$ 的金字塔式生成，不同层级的贡献肯定是不同的。

$t_{box}(l)$ 为采样第 $l$ 层 $mipmap$ 的加权采样函数。

$B(l,x,y)$ ：第 $l$ 层 $mipmap$ 的权重。

又因为 $mipmap$ 由每层的四个像素求平均值以生成下一层的像素，因此每层的权重都是上一层的四分之一。然后将边界条件转为为一个同时包含 $x,y,l$ 的边界条件，虽然该边界条件更加准确的做法应该根据式 $(6)$ 的边界条件所围成的面积来计算，但为了方便后续的计算贴合一维高斯滤波函数，可以近似成式 $(7)$ 的形势，该近似对结果的影响非常小：

$N$ ：盒子的尺寸，由 $mipmap$ 的层级 $l$ 所决定的，即 $N=2^l * 2^l$ 。

由上式可以看出采样点的坐标 $(x,y)$ 与采样的层级 $l$ 存在的不等式关系。

将以上公式代回式 $(4)$ 的盒型滤波采样公式：

和高斯滤波采样公式相比，显然可以看出盒型滤波函数和高斯滤波函数的关系。再将式 $(7)$ 求得的边界条件带入界，即可得到和 $mipmap$ 的层级 $L$ 有关的高斯滤波函数，同时可以看出对边界条件的近似的目的就是为了方便高斯函数的计算：

假设 $w(l)4^{-l}$ 的原函数为 $g(l)$ ，即 $g'(l)=w(l)4^{-l}$ ，由牛顿-莱布尼兹公式和式 $(9)$ 可得 ：

由于层级越大，盒型滤波的权重越小。故式 $(10)$ 的极限结果应为 $0$。因此可得高斯滤波函数与盒型滤波函数的关系为：

由 $g'(l)=w(l)4^{-l}$ 或对式 $(9)$ 求导皆可得出权重 $w(l)$ 与层级 $l$ 的关系式及其原函数，再由权重 $w(l)$ 及其原函数可以得出第 $L$ 层的混合权重 $\alpha(L)$ 。

代码实现

GLSL代码实现

#version 430 core
#define PI 3.141592654
in  vec2 v2f_TexCoords;
out vec4 Color_;

uniform sampler2D u_SourceTexture;
uniform sampler2D u_CoarserTexture;
uniform vec2	g_focus = vec2(0);
uniform	float	g_sigma = 5.0;
uniform int	g_level = 0;

求混合参数：float MipGaussianBlendWeight(vec2 tex)

1. 首先依据纹理坐标生成高斯函数的标准差 $\sigma$ 和方差 $\sigma^2$ 。

float sigma = g_sigma;
if (uint(g_focus.x) != 0xffffffff)
{
    const vec2 r = (2.0 * tex - 1.0) - g_focus; //(0，1)^2 to (-1,1)^2
    sigma *= dot(r, r);//length of vector r
}
const float sigma2 = sigma * sigma;

2. 由 $\alpha (L)$ 的公式先求出分子部分： ${16^{L} \ln 4}$ 。

const float numerator = (1 << (g_level << 2)) * log(4.0);

3. 求出 $\alpha (L)$ 公式的分母部分： $2 \pi \sigma^{2}\left(4^{L}+2 \pi \sigma^{2}\right)$ 。

const float c = 2.0 * PI * sigma2;
const float denominator = c * ((1 << (g_level << 1)) + c);

4. 返回混合权重 $\alpha (L)$ ，并确保 $\alpha (L)$ 的范围在 $(0,1)$ 。

return clamp(numerator / denominator,0,1);

主函数：void main()

1. 只生成到第 10 层，到第10层后结束递归。

if(g_level == 10)
{
    Color_ = textureLod(u_CoarserTexture, v2f_TexCoords,10).rgba;
    return ;
}

2. 获取第 $L$ 层的混合权重 $\alpha (L)$ 。

float alpha = MipGaussianBlendWeight(v2f_TexCoords);

3. 获取当前层和下一层的 $mipmap$ 。

vec3 color_source = textureLod(u_SourceTexture, v2f_TexCoords,g_level + 1).rgb;
vec3 color_coarser = textureLod(u_CoarserTexture, v2f_TexCoords,g_level).rgb;

4. 由公式 $(1-\alpha(L)) p(x, L+1)+\alpha(L) p_{\text {down }}(x, L)$ 求出纹理颜色值。

Color_ = vec4((1 - alpha) * color_source + alpha * color_coarser, 1.0f);