参与11月更文挑战的第11天，活动详情查看：2021最后一次更文挑战

为什么需要激活函数呢？

用下边这个神经网络分析一下：

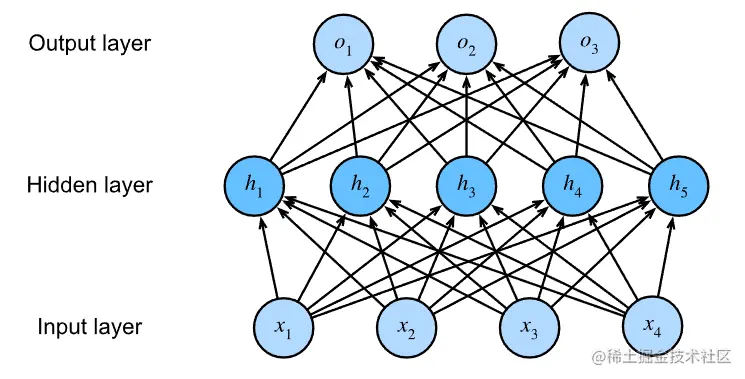
对于上图： 我们知道其中 $X^{4 \times 1} \quad H^{5 \times 1} \quad O^{7 \times 1}$

其中各层之间的计算：

将上边两个计算公式合并：

再看看其矩阵运算：

$[w_{2}]_{3 \times 5} \cdot [w_{1}]_{5 \times 4} =[w]_{3 \times 4}$

$[w_{2}]_{2 \times 5} \cdot [b_{1}]_{5 \times 1} =[b_{1^{\prime}}]_{3 \times 1}$

$[b_{1^{\prime}}]_{3 \times 1}+[b_{2}]_{3 \times 1} =[b]_{3 \times 1}$

再把算出来的矩阵带回合并计算的公式里边，就又变成了$O=wX+b$。这样的话这个多层神经网络就完全没有存在的意义了，既然能合并，那直接写成一层不香吗？香！但是多层模型又有一些单层做不到的事情，那如何保留多层模型使之不能被简单地合并呢？那就用到了激活函数。

ReLU函数（Rectified linear unit）

公式：$\operatorname{ReLU}(x) = \max(x, 0)$

$\sigma(x)= \begin{cases}x & \text { if } x>0 \\ 0 & \text { otherwise }\end{cases}$

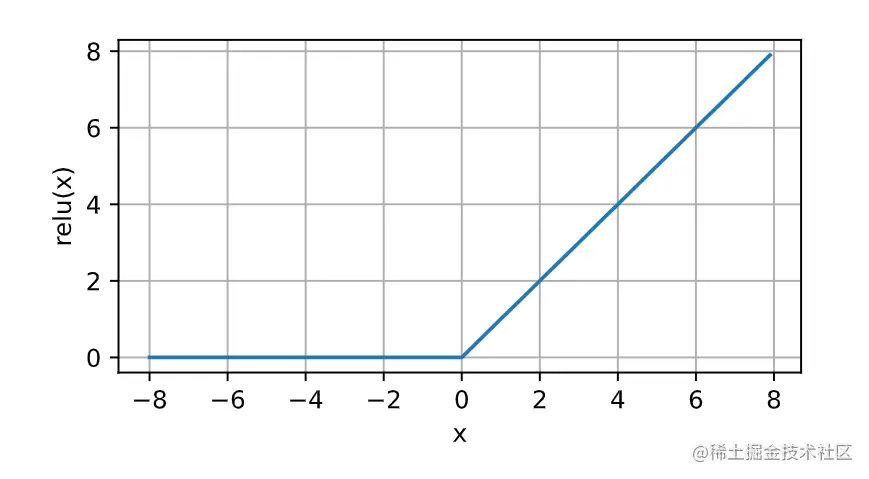
ReLU函数通过将相应的激活值设为0来仅保留正元素并丢弃所有负元素。

经过ReLU处理的函数长这样：

Sigmoid函数

然后是我学习接触到的第一个激活函数，当时听的吴恩达的课，他有详细的讲到使用sigmoid的好处，我还记了笔记，可以看这里：逻辑回归 | Logistic Regression - 掘金 (juejin.cn)

公式：$\operatorname{sigmoid}(x) = \frac{1}{1 + \exp(-x)}$

$\sigma(x)= \begin{cases}1 & \text { if } x>0 \\ 0 & \text { otherwise }\end{cases}$

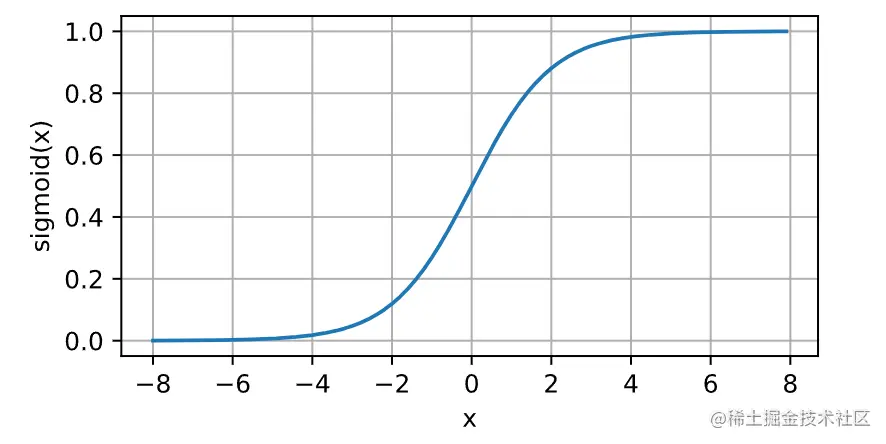
对于一个定义域在$\mathbb{R}$中的输入，sigmoid函数将输入变换为区间(0, 1)上的输出。因此，sigmoid通常称为挤压函数（squashing function）：它将范围(-inf, inf)中的任意输入压缩到区间(0, 1)中的某个值。

tanh函数

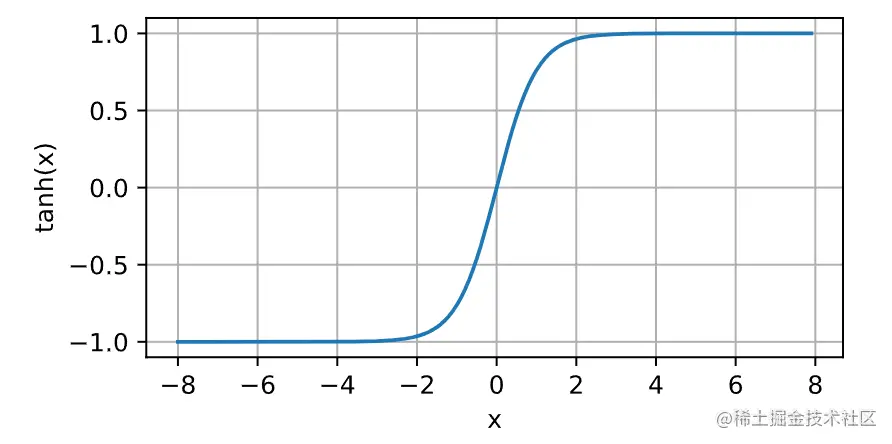
公式：$\operatorname{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}$

与sigmoid函数类似，tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上。