这是我参与8月更文挑战的第20天,活动详情查看:8月更文挑战
Logistic Regression
跟线性回归不同,在这里要预测的y是离散值。
用到的 Logistic Regression 算法是当今最流行最广泛使用的学习算法之一。
还记得监督学习和无监督学习的分类吗
Classification
Emai:Spam/ Not Spam?
Online Transactions:Fraudulent(Yes/No)?
Tumor:Malignant/ Benign
邮件:是否是垃圾邮件
网上交易:是否存在欺诈
肿瘤分类:良心恶性
记得的话就会知道上述都属于离散型监督学习。上述三个问题的共同之处:
y∈{0,1}
0:Negative Class"
1:"Positive Class"
当然并不是所有的离散型问题都非黑即白只有两个结果,也有可能是y∈{0,1,3,...,n}可数有限多个。
举个例子
从简单的二类离散开始:
从肿瘤的大小预测其是良性还是恶性:
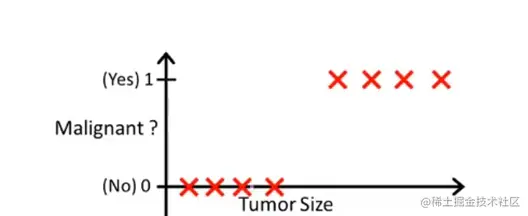
如果我们还是用线性回归的方法拟合是无法生效的。比如像这样:
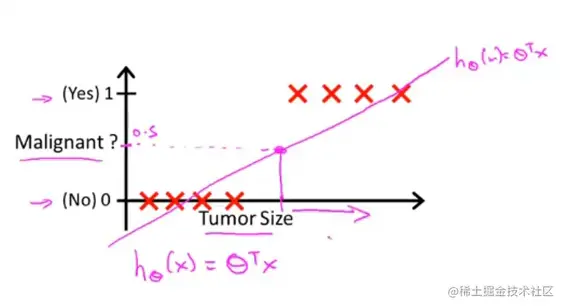
现在我们对于这条拟合直线假定h(x)>0.5为恶性,反之为良性。你可能说这不是拟合的挺好的吗。
但是如果这样呢:
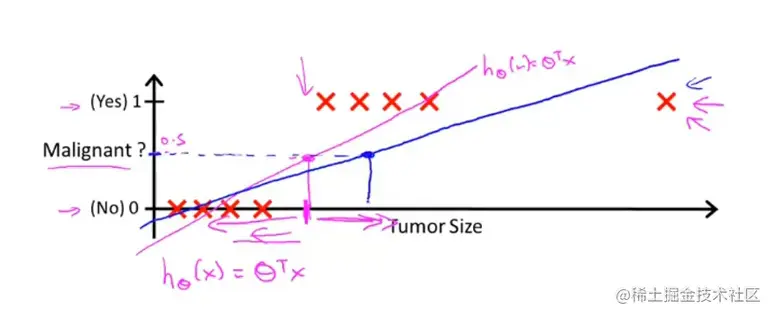
就会有很多恶心的肿瘤被判断为良性。
所以说线性回归并不适合离散型问题。
逻辑回归
那对于离散回归怎么办呢。首先我们要确保:
0≤hθ(x)≤1
这样就不会出现线性回归那样的问题。线性回归中不管你怎么拟合。只要超出一定范围总会出现h(x)>1的情况。
那要如何改良呢?
这就借助到Sigmoid function又称Logistic function:
g(z)=1+e−z1
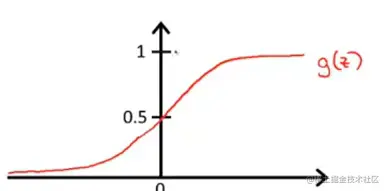
再将线性回归的公式应用到Logistic函数中后得到:
hθ(x)=g(θTx)=1+e−θTx1
现在已经知道如何将hθ(x)的值固定在0~1之间,那对于输出结果怎么描述呢?
Estimated probability that y = 1 on input x。
描述输入x对于y = 1时结论的可能性。
比如y = 1代表恶性肿瘤,用户x输入得到的结果为0.7。
你不能说“恭喜你,你得恶性肿瘤了”,而是要说“你得恶性肿瘤的概率是70%”。
正规结果用概率的方式表示就是:
hθ(x)=P(y=1∣x;θ)
上面的式子我们还可以推出hθ(x)=P(y=1∣x;θ)+hθ(x)=P(y=0∣x;θ)=1
决策边界
刚才上边说到描述结果,要说x的输入对于y=1时候的可能性。但是严格意义上来说并不是所有的都要说是对于y=1时候的可能性。
Suppose :
- predict y=1 if hθ(x)≥0.5
- predict y=0 if hθ(x)<0.5
一般来说,hθ(x)大于等于0.5就说相对于y=1的结论,小于0.5说相对于0的结论。
注意区分一下逻辑,比如x输入之后y=0.2,你不能说你有20%的几率是恶性肿瘤,而是说你有80%几率是良性肿瘤。
上边的说法还可以等价为
Suppose :
- predict y=1 if θTx≥0
- predict y=0 if θTx<0
因为上边的g(z)=1+e−z1的图像,z>0时候为正,z<0为负。而hθ(x)=g(θTx),所以可以进行如上转换。
而决策边界就是θTx=0的时候。
画个图像更直观的了解一下:
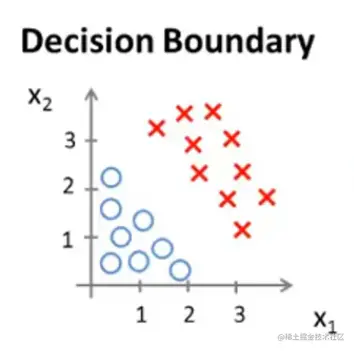
上图假设我们已经找到预测函数hθ(x)=θ0+θ1x1+θ2x2,其中θ=⎣⎡−311⎦⎤,带入就是hθ(x)=−3+x1+x2
你现在不用管预测函数是怎么出来的,文章下边会讲的
其中θTx=−3+x1+x2=0就是x1+x2=3这条直线。这条直线就是决策边界。而这条线上边的红叉叉区域就是x1+x2>3的区域,被称为y=1区域。反之下边蓝圈圈就是y=0区域。
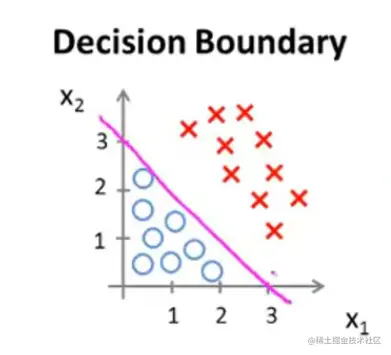
The decision boundary is a property of the hypothesis.
决边界是假设函数的一个属性,跟数据无关。也就是说虽然我们需要数据集来确定θ的取值,但是一旦确定以后,我们的决策边界就确定了,剩下的就和数据集无关了,图像上也不一定非要把数据集可视化。
现在来个更复杂的例子:
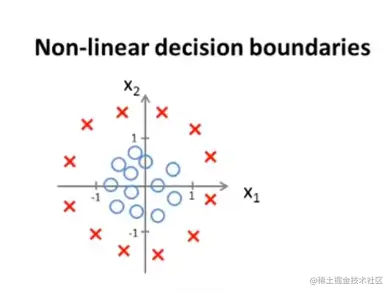
对于这个图像我们的预测函数是hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22)
,其中θ=⎣⎡−10011⎦⎤
y = 1 的时候就是x12+x22≥1
y = 0 的时候就是x12+x22<1
这个例子中决策边界就是x12+x22=1
如何拟合Logistic Regression
Training set:
{(x(1),y(1)),(x(2),y(2)),⋯,(x(m),y(m))}
m examples x∈⎣⎡x0x1…xn⎦⎤x0=1,y∈{0,1}
hθ(x)=1+e−θTx1
How to choose parameters θ ?
先说我们的训练集,是m个点。跟之前一样把x列成一个矩阵,并且加上一个x0=1,θTx=θ0X0+θ1x1+...+θnxn
那如何选择θ?
要计算θ首先要找到代价函数。
代价函数
还记得线性回归的代价函数吗?
J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2
换一种写法,用
Cost(hθ(x),y)=21(hθ(x)−y)2
Cost(hθ(x),y)代表预测函数和实际值的差,代价函数J则表示对所有训练样本和预测函数的代价求和之后取平均值。
所以线性回顾代价函数还可以写为:
J(θ)=m1∑i=1mCost(hθ(x),y)
在离散值里如果你继续使用这个代价函数,那画出图像以后结果是个非凸函数。长下边这样,也就是说你没办法顺利的找到最优解。
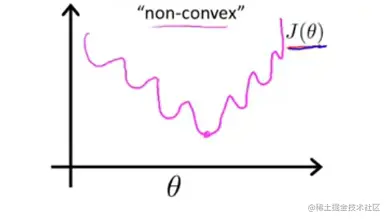
所以我们需要找一个凸函数来作为逻辑回归的代价函数:
Logistic regression cost function
Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x)) if y=1 if y=0
如果y=1图像如下:
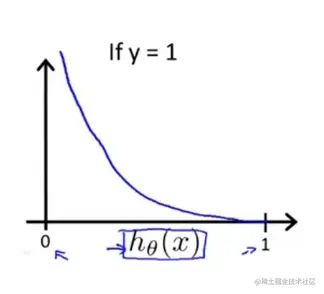
我们知道h(x)的取值范围在0~1之间,结合log图像的特点,我们就可理解上述图像是怎么出现的了。
这个函数有一些很有趣的优秀性质:
Cost=0:ify=1,hθ(x)=1
当代价函数等于0的时候,也就是我们的假设函数hθ(x)=1,即我们预测是恶性肿瘤,并且实际数据y=1,即病人确实是恶性肿瘤。也就是说代价函数0,我们预测正确。
Butashθ(x)→0,Cost→∞
但是如果我们的假设函数趋于0的时候,代价函数却趋于正无穷。
Captures intuition that if hθ(x)=0
(predict P(y=1∣x;θ)=0), but y=1, we'll penalize learning algorithm by a very large cost.
如果假设函数等于0相当于说对于y=1即病人的恶性肿瘤这件事,我们预测的概率是0。
如果放到现实生活中就相当于我们对病人说:你完全不可能是恶性肿瘤!现实中如果肿瘤确实是恶性,那医生的话就是重大医疗事故。医生要付出很大代价。但是在这个函数中只能趋于0,不会等于0。
再看看y=0的情况:
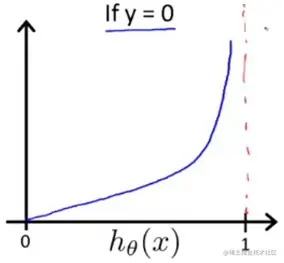
Cost=0:ify=0,hθ(x)=0
代价函数0,y=0代表病人是良性肿瘤,我们预测函数hθ(x)=0说明我们预测的肿瘤是良性,预测完全正确,所以代价函数0.
Butashθ(x)→0,Cost→∞
Captures intuition that if hθ(x)=1
(predict P(y=0∣x;θ)=1)
y=0代表病人良性肿瘤,但是我们预测函数等于1的话,说明我们预测的是恶性肿瘤,告诉病人:你不可能是良性肿瘤。在生活中万一人家是良性肿瘤,医生这句话又会造成不必要恐慌……
所以这个函数的有趣又优良之处在于不能把话说的太满。
上边已经说到代价函数了:
Logistic regression cost function
J(θ)=m1∑i=1mCost(hθ(x(i)),y(i))
Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x)) if y=1 if y=0
Note: y=0 or 1 always
现在我们将其简化:
cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
为什么简化之后就是这个式子?
直接带数进上边式子就可以了。
- y = 1:cost(hθ(x),1)=−1log(hθ(x))−(1−1)log(1−hθ(x))=−log(hθ(x))
- y = 0:cost(hθ(x),0)=0log(hθ(x))−(1−0)log(1−hθ(x))=−log(1−hθ(x))
所以就是直接将上边两个式子合并成一个式子,不需要再来判断y的取值情况分类进行了。
现在我们就可以写出逻辑回归的代价函数:
Logistic regression cost function
J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))=−m1[i=1∑my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
根据这个代价函数,我们要找到minθJ(θ),即让代价函数取得最小值的参数θ。
那就又要进行梯度下降了。
梯度下降
Gradient Descent
J(θ)=−m1[i=1∑my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
Want minθJ(θ):
Repeat {
θj:=θj−α∂θj∂J(θ)
}
(simultaneously update all θj )
对上述的J(θ)求偏导之后带入梯度下降公式,最后得到如下形式:
Gradient Descent
J(θ)=−m1[i=1∑my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
Want minθJ(θ):
Repeat {
θj:=θj−αi=1∑m(hθ(x(i))−y(i))xj(i)
(simultaneously update all θj )
emmmmm现在你有没有发现一个问题,逻辑回归的梯度下降公式和线性回归梯度下降公式看起来一模一样。
为什么加粗了看起来,因为毕竟他们的预测函数不同。
hθ(x)=θTxhθ(x)=1+e−θTx1
所以说虽然看起来一样,但实际还是天差地别。
高级优化
讲线性回归的时候我们说找最佳的θ除了使用梯度下降,还可以使用正规方程。对于逻辑回归也是如此,我们除了使用梯度下降,还可以使用别的算法。(下边列举的这三种都需要代价函数和代价函数的偏导。区别是跟梯度下降迭代部分不一样)
- Conjugate gradient
- BFGS
- L-BFGS
Advantages:
- No need to manually pick α
- Often faster than gradient descent Disadvantages:
- More complex
这三个算法相对于梯度下降,有点事不需要选择学习速率α并且比梯度下降更快。缺点是算法更为复杂。
当然更为复杂这个根本不是缺点,因为你不需要知道原理,直接用别人已经写好的就行了。吴恩达老师原话“我用了十多年了,然而我前几年才搞清楚他们的一些细节。”
想起来一个好笑的梗:贵的东西只有一个缺点那就是贵,但这不是东西的缺点,是我的缺点。
octave和MATLAB有这种库,直接用就行了。至于你使用C,C++,python之类的,那你可能要多试几个库才能找到实现比较好的。
如何应用到逻辑回归中?
theta =⎣⎡θ0θ1⋮θn⎦⎤
function [jVal, gradient] = costFunction (theta)
jVal=[ code to compute J(θ)];
gradient (1)=[ code to compute ∂θ0∂J(θ)]
gradient (2)=[ code to compute ∂θ1∂J(θ)]
...
gradient (n+1)=[ code to compute ∂θn∂J(θ)]
举个例子:
Example: θ=[θ1θ2]J(θ)=(θ1−5)2+(θ2−5)2∂θ1∂J(θ)=2(θ1−5)∂θ2∂J(θ)=2(θ2−5)
现在有一个含两个参数的实例,肉眼可见当代价函数最小(等于0)的时候两个θ都等于5。好嘛,现在是为了学算法,我们假装不知道结果。
function [j,gradient] = costFunction(theta)
%代价函数J
j = (theta(1)-5)^2 + (theta(2)-5)^2;
gradient = zeros(2,1);
%偏导
gradient(1) = 2*(theta(1)-5);
gradient(2) = 2*(theta(2)-5);
endfunction
costFunction函数有两个返回值。一个是代价函数J,一个是对J求偏导,用于存储结果的向量。
%octave中输入:
options = optimset ('GradObj','on','MaxIter','100');
initheta = zeros(2,1);
[Theta,J,Flag] = fminunc (@costFunction,initheta,options)
- optimset:进行设置,其中四个参数:
- GradObj:设置梯度目标参数
- 确认上一步设置开启
- 最大迭代次数
- 设置最大迭代次数值
- fminunc:octave的无约束最小化函数,需要传入三个参数
- 你自己写的函数,前边一定要加@
- 你预设的θ,必须是一个二维及以上的向量,如果是一个实数,该函数会失效。
- 对该函数的设置
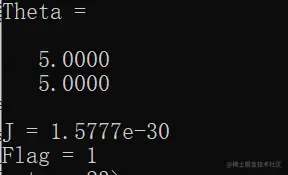
最后运行结果长这样,Theta存储最终的代价函数最小化时θ的取值。J表示代价函数最优解,Flag = true表示已经收敛。
多类分类 Multiclass classification
什么是多类分类?
比如你又一个邮件要对他自动分类为:工作、朋友、家庭、其他。

对这种分类怎么处理?
Using an idea called one-versus-all classification, we can then take this and make it work for muti-class classification, as well.
利用一对多的分类思想,我们同样可以把二类分类的思想应用在多类别分类上。
Here's how one-versus-alll classiffication works. And, this is also sometimes called one-versus-rest.
现在介绍一下敌对多分类方法(一对余):
Let's say, we have a training set
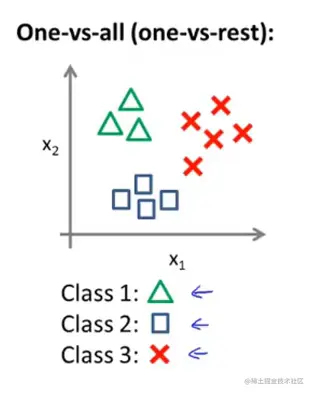
用三角表示1,方块表示2,叉表示3
现在将其改为三个独立的二元分类:
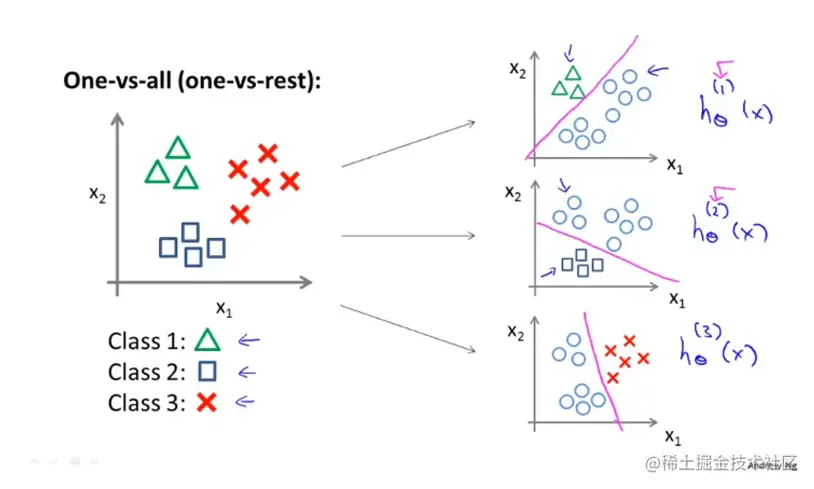
hθ(i)(x)=P(y=i∣x;θ)(i=1,2,3)
在这里表i=1的时候就是三角形做正类的时候。上述i个分类器对其中每一种情况都进行了训练。
在一对多分类中
One-vs-all
Train a logistic regression classifier hθ(i)(x) for each class i to predict the probability that y=i
On a new input x, to make a prediction, pick the class i that maximizes
imaxhθ(i)(x)
我们获得一个逻辑回归分类器,hθ(i)(x)预测i类别在y=i时候的概率。最后做出预测,我们给出一个新的输入值x,想获得预测结果,我们要做的就是在每个分类器中运行输入x,最后选择预测函数最大的类别,就是我们要预测的结果y。