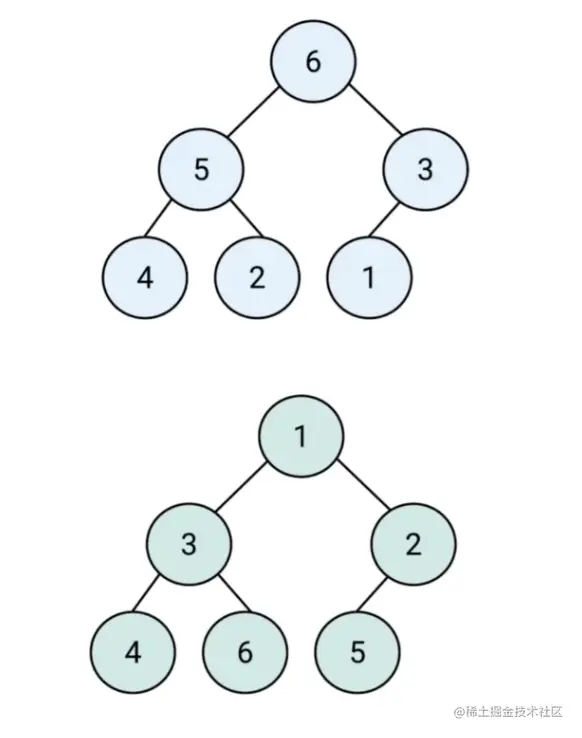
堆简介

• 堆是一个特殊的完全二叉树
• 所有的节点都大于（最大堆）或 小于等于（最小堆）它的子节点
• js中通常用数组表示堆

堆表示法和堆特点

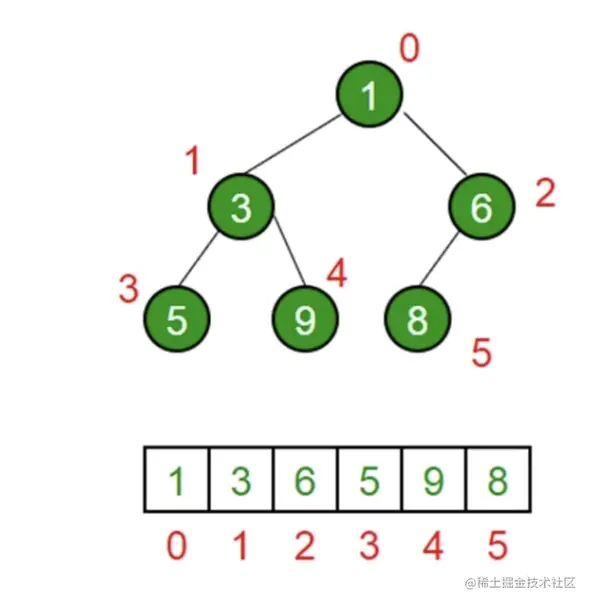
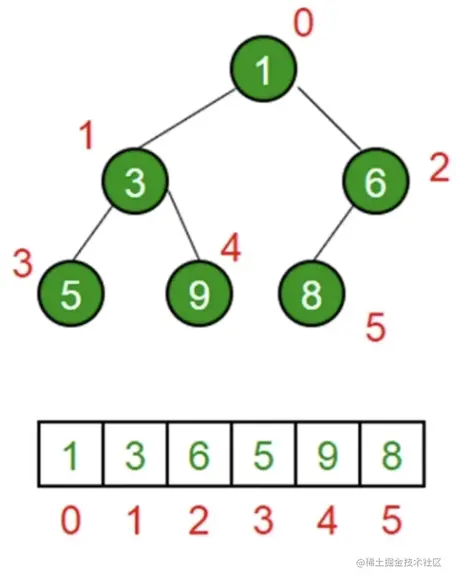
• js中通常用数组表示堆
• 左侧子节点的位置（下标）是 2 * index + 1
• 右侧子节点的位置（下标）是 2 * index + 2
• 父节点的位置(下标)是 (index -1)/2

堆的应用

• 堆能高效、快速的找出最大值和最小值， 时间复杂度O(1)
• 找出第k个最大（小）元素

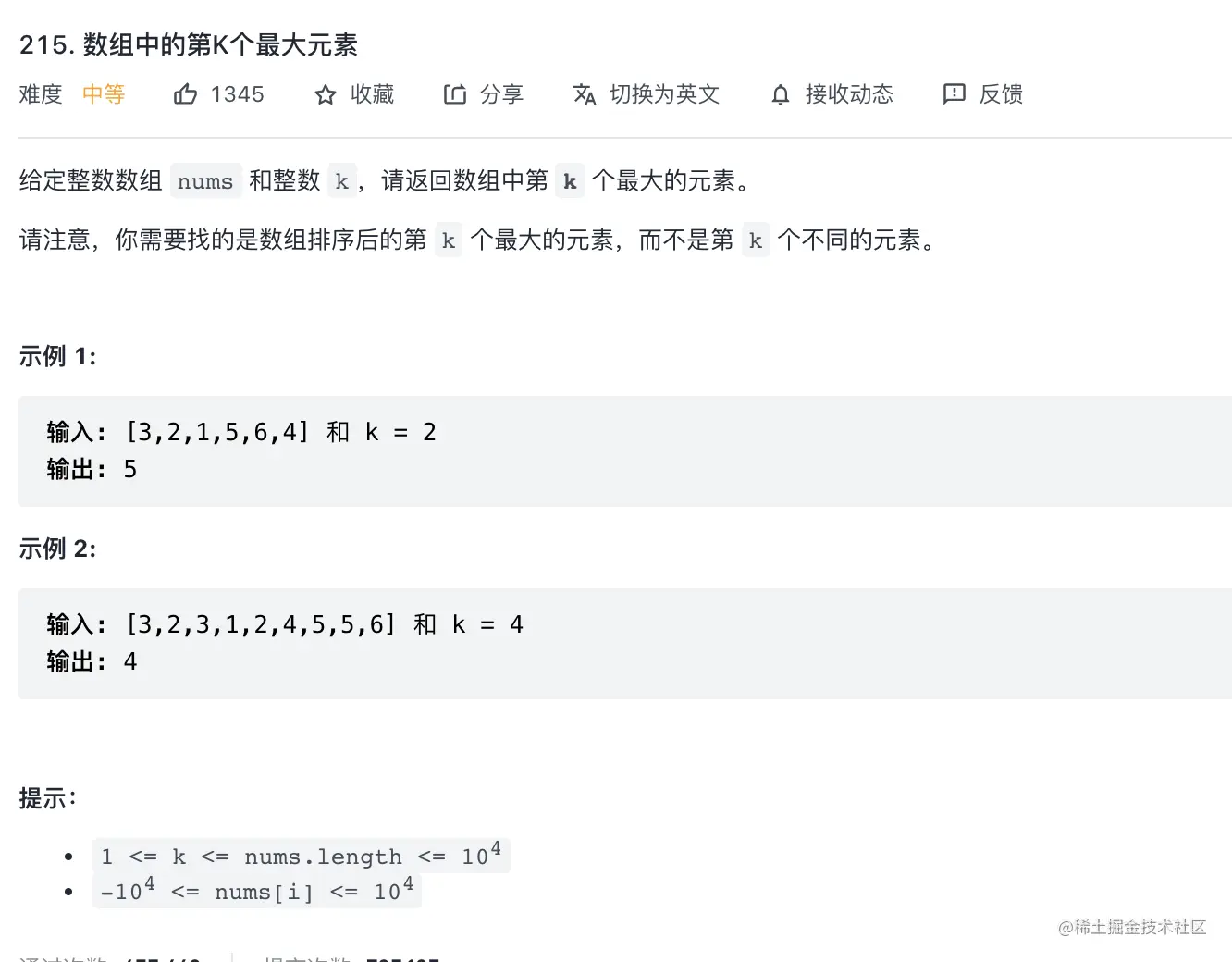
第k个最大元素

• 构建一个最小 堆，并将元素依次插入堆中
• 当堆的容量超过k，就删除堆顶
• 插入结束后，堆顶就是第k个最大元素

js 实现最小堆类

• 在类里，声明一个数组，用来装元素
• 主要方法： 插入、删除堆顶、获取堆顶、获取堆大小

插入

• 将值插入堆的底部，即数组的尾部
• 然后上移： 将这个值和它的父节点进行交换，直到父节点小于等于这个插入的值
• 大小k的堆中插入元素的时间复杂度为O(logk)

删除堆顶

• 用数组尾部元素替换堆顶（直接删除堆顶会破坏堆结构）
• 然后下移：将新的堆顶和它的子节点交换，直到子节点大于等于这个新的堆顶
• 大小为k的堆中删除堆顶的时间复杂度为O(logk)

获取堆顶和堆的大小

• 获取堆顶： 返回数组的头部
• 获取堆的大小： 返回数组的长度

class MinHeap {
  constructor() {
    this.heap = [];
  }
  swap(i1, i2) {
    const temp = this.heap[i1];
    this.heap[i1] = this.heap[i2];
    this.heap[i2] = temp;
  }
  getLeftIndex(index) {
    return index * 2 + 1;
  }
  getRightIndex(index) {
    return index * 2 + 2;
  }
  getParentIndex(index) {
    // Math.floor((index -1) / 2);
    return (index - 1) >> 1;
  }
  _shiftUp(index) {
    if (index === 0) return;
    const parentIndex = this.getParentIndex(index);
    if (this.heap[parentIndex] > this.heap[index]) {
      this.swap(parentIndex, index);
      // 上移完成索引 已经是父节点索引了
      this._shiftUp(parentIndex);
    }
  }
  //下移操作
  _shiftDown(index) {
    const leftIndex = this.getLeftIndex(index);
    const rightIndex = this.getRightIndex(index);
    if (this.heap[leftIndex] < this.heap[index]) {
      this.swap(index, leftIndex);
      this._shiftDown(leftIndex);
    }
    if (this.heap[rightIndex] < this.heap[index]) {
      this.swap(index, rightIndex);
      this._shiftDown(rightIndex);
    }
  }
  insert(value) {
    this.heap.push(value);
    this._shiftUp(this.heap.length - 1);
  }
  pop() {
    this.heap[0] = this.heap.pop();

    this._shiftDown(0);
  }
  get peek() {
    return this.heap[0];
  }
  get size() {
    return this.heap?.length;
  }
}
const h = new MinHeap();
h.insert(7);
h.insert(10);
h.insert(2);
h.pop();
console.log(h.size, "heap");

leetcode-cn.com 算法题实战

完整题目请打开 leetcode

215. 数组中的第K个最大元素

解题思路

• 看到“第k个最大元素”
• 考虑选择使用最小堆
• 构建一个最小堆，并依次把数组的值插入堆中
• 当堆的容量超过k,就删除堆顶
• 插入结束后，堆顶就是第k个最大元素

class MinHeap {
  constructor() {
    this.heap = [];
  }
  swap(i1, i2) {
    const temp = this.heap[i1];
    this.heap[i1] = this.heap[i2];
    this.heap[i2] = temp;
  }
  getLeftIndex(index) {
    return index * 2 + 1;
  }
  getRightIndex(index) {
    return index * 2 + 2;
  }
  getParentIndex(index) {
    // Math.floor((index -1) / 2);
    return (index - 1) >> 1;
  }
  _shiftUp(index) {
    if (index === 0) return;
    const parentIndex = this.getParentIndex(index);
    if (this.heap[parentIndex] > this.heap[index]) {
      this.swap(parentIndex, index);
      // 上移完成索引 已经是父节点索引了
      this._shiftUp(parentIndex);
    }
  }
  //下移操作
  _shiftDown(index) {
    const leftIndex = this.getLeftIndex(index);
    const rightIndex = this.getRightIndex(index);
    if (this.heap[leftIndex] < this.heap[index]) {
      this.swap(index, leftIndex);
      this._shiftDown(leftIndex);
    }
    if (this.heap[rightIndex] < this.heap[index]) {
      this.swap(index, rightIndex);
      this._shiftDown(rightIndex);
    }
  }
  insert(value) {
    this.heap.push(value);
    this._shiftUp(this.heap.length - 1);
  }
  pop() {
    this.heap[0] = this.heap.pop();

    this._shiftDown(0);
  }
  get peek() {
    return this.heap[0];
  }
  get size() {
    return this.heap?.length;
  }
}
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var findKthLargest = function(nums, k) {
    const h = new MinHeap();
    nums.forEach(n => {
        h.insert(n);
        if(h.size > k) {
            h.pop();
        }
    })
    return h.peek;
};

347. 前 K 个高频元素

class MinHeap {
  constructor() {
    this.heap = [];
  }
  swap(i1, i2) {
    const temp = this.heap[i1];
    this.heap[i1] = this.heap[i2];
    this.heap[i2] = temp;
  }
  getLeftIndex(index) {
    return index * 2 + 1;
  }
  getRightIndex(index) {
    return index * 2 + 2;
  }
  getParentIndex(index) {
    // Math.floor((index -1) / 2);
    return (index - 1) >> 1;
  }
  _shiftUp(index) {
    if (index === 0) return;
    const parentIndex = this.getParentIndex(index);
    if (this.heap[parentIndex] && this.heap[parentIndex].value > this.heap[index].value) {
      this.swap(parentIndex, index);
      // 上移完成索引 已经是父节点索引了
      this._shiftUp(parentIndex);
    }
  }
  //下移操作
  _shiftDown(index) {
    const leftIndex = this.getLeftIndex(index);
    const rightIndex = this.getRightIndex(index);
    if (this.heap[leftIndex] && this.heap[leftIndex].value < this.heap[index].value) {
      this.swap(index, leftIndex);
      this._shiftDown(leftIndex);
    }
    if (this.heap[rightIndex] && this.heap[rightIndex].value < this.heap[index].value) {
      this.swap(index, rightIndex);
      this._shiftDown(rightIndex);
    }
  }
  insert(value) {
    this.heap.push(value);
    this._shiftUp(this.heap.length - 1);
  }
  pop() {
    this.heap[0] = this.heap.pop();

    this._shiftDown(0);
  }
  get peek() {
    return this.heap[0];
  }
  get size() {
    return this.heap?.length;
  }
}
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var topKFrequent = function(nums, k) {
    const map = new Map();
    nums?.forEach(n => {
        map.set(n, map.has(n) ? map.get(n) + 1 : 1)
    })
    const h = new MinHeap();
    map.forEach((value,key) => {
        h.insert({value, key});
        if(h.size > k) {
            h.pop();
        }
    })
    return h.heap.map(a => a.key);
};

下一站 排序算法