[算法&数据结构]排序算法--堆排序(Java版)

堆排序

分为大根堆和小根堆，其中升序排列使用大根堆，降序排列使用小根堆。

使用到的数据结构：完全二叉树

注：完全二叉树是依次排列节点的二叉树；

完美二叉树：叶子节点都在同一层的完全二叉树；

堆排序：核心问题就是初始化大根堆，还有交换，调整大根堆的过程。

时间复杂度：O(nlogn)

算法流程：

1. 调整大根堆
2. 置换根结点：将树根元素和最末尾元素置换，确定最大值位置
3. 调整新根结点位置：将新置换的树根结点调整到合适位置，保持大根堆属性
4. 重复2,3步骤，直到遍历完整个二叉树

构建大根堆算法示意图如下：

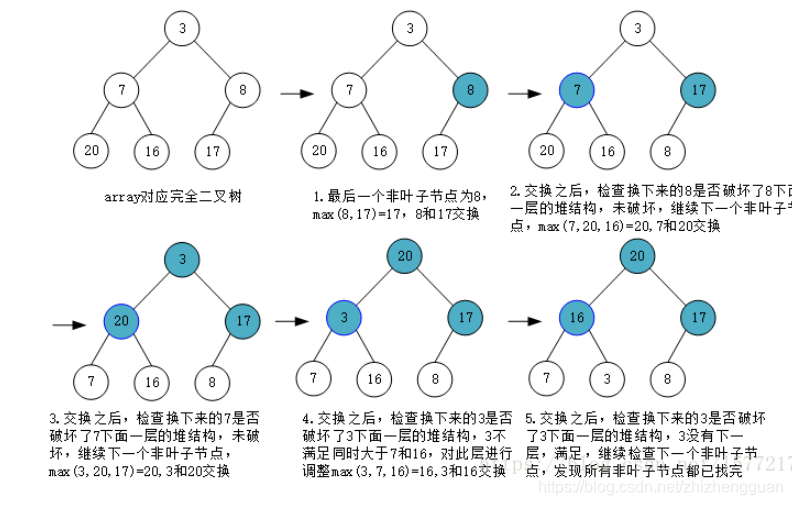
实现代码如下：

/***
 * 堆排序
 * 使用二叉树模式
 * 堆是一种完全二叉树，大根堆，是每轮迭代之后，根节点是最大数，和最末尾的叶子节点进行置换。
 * 堆排序的平均时间复杂度为 Ο(nlogn)。
 */
public class HeapSort {
    public static void main(String[] args) {
        // 初始化随机数组
        int[] data = new int[8];
        for (int i = 0; i < 8; i++){
            data[i] = new Random().nextInt(20) + 1;
        }
        // 进行堆排序(顺序)
        HeapSort.heapSord(data);
    }

    // 堆排序主流程
    public static int[] heapSord(int[] data){
        // 当前需维护堆属性的队列长度
        int len = data.length - 1;

        /**
         * 步骤一：构建大根堆
         * 从最后一个非叶子结点开始遍历，调整符合大根堆属性（叶子结点不需要比对）
         * */
        int end = len / 2 - 1;   // 最后一个非叶子结点
        for (int i = end ; i >= 0 ; i--){
            heapAdjust(data,len,i);
        }

        /**
         * 步骤二：置换最大值，调整大根堆
         * */
        for(int i = data.length - 1; i > 0 ; i --){
            // 第一个元素(最大值)置换为最末尾值
            int tmp_value = data[0];
            data[0] = data[i];
            data[i] = tmp_value;
            // 待比对数组长度减小1(最末尾的元素已经确定)
            len --;
            heapAdjust(data,len,0);

        }
        return data;
    }

    /**
     * 调整堆中元素的具体位置
     * int[] data：原始数据
     * int len：待调整的数组总长度
     * int index：待调整元素下标
     * */
    private static void heapAdjust(int[] data,int len,int index){
        // 判断当前结点和左右子节点中最大元素的下标
        int tmp_index = max(data,len,index);
         /**
         * 递归函数结束条件:当前结点最大，不需要做调整
         * */
        if (tmp_index == index){
            return;
        }

        // 交换最大值
        int tmp_value = data[index];
        data[index] = data[tmp_index];
        data[tmp_index] = tmp_value;
        // 递归调整到最终结果
        heapAdjust(data,len,tmp_index);
    }
    // 获取当前index结点，和左右结点中，最大元素下标
    private static int max(int[] data,int len,int index){
        int max = index;
        // 左结点下标
        int left = index * 2 + 1;
        // 右结点下标
        int right = index * 2 + 2;
        // 需确保左右子节点均存在
        if (left < len && data[left] > data[max]){
            max = left;
        }

        if (right < len && data[right] > data[max]){
            max = right;
        }
        return max;
    }
}