GGX重要性采样 - 闪之剑圣 - 博客园 (cnblogs.com)
PBR（基于物理的渲染）学习笔记2 - 木的树 - 博客园 (cnblogs.com)
反射方程
镜面反射部分
简化 分割求和近似法
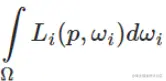预滤波环境贴图
- 用一个点取范围的点,然后平均来模糊这个点,然后就获得新的图,在球面上做的filtter
- 只考虑正半球所有方向的(与点的法线的点乘是正的半球)
- 用蒙特卡洛的方式解决积分,满足任何分布的pdf,数值上的近似,但需要大量的数据才能接近期望
- 一般有sampling 一般不能用在实时渲染中,一般都避免sampling(采样)
重要性采样
- 镜面反射的方向,spcular lobal,
- 已知公式
- 转换球坐标系的概率密度函数
// Based on http://blog.selfshadow.com/publications/s2013-shading-course/karis/s2013_pbs_epic_slides.pdf
// 将一个二维采样序列转换成三维空间中的采样方向
vec3 importanceSample_GGX(vec2 Xi, float roughness, vec3 normal)
{
// 基于粗糙度将二维点映射到半球 球与极坐标
float alpha = roughness * roughness;
float phi = 2.0 * PI * Xi.x + random(normal.xz) * 0.1;
float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (alpha*alpha - 1.0) * Xi.y));
float sinTheta = sqrt(1.0 - cosTheta * cosTheta);
vec3 H = vec3(sinTheta * cos(phi), sinTheta * sin(phi), cosTheta);
// 切线空间
vec3 up = abs(normal.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
vec3 tangentX = normalize(cross(up, normal));
vec3 tangentY = normalize(cross(normal, tangentX));
// 转换到世界空间
return normalize(tangentX * H.x + tangentY * H.y + normal * H.z);
}
GGX 法线分布函数
float D_GGX(float dotNH, float roughness)
{
float alpha = roughness * roughness;
float alpha2 = alpha * alpha;
float denom = dotNH * dotNH * (alpha2 - 1.0) + 1.0;
return (alpha2)/(PI * denom*denom);
}
蒙特卡洛与pdf
- 蒙特卡洛积分最关键的就是找出一个合适的概率密度函数
- pdf 代表概率密度函数 (probability density function)，它的含义是特定样本在整个样本集上发生的概率。
float pdf = D_GGX(dotNH, roughness) * dotNH / (4.0 * dotVH) + 0.0001;
float omegaS = 1.0 / (float(consts.numSamples) * pdf);
原文
#version 450
layout (location = 0) in vec3 inPos;
layout (location = 0) out vec4 outColor;
layout (binding = 0) uniform samplerCube samplerEnv;
layout(push_constant) uniform PushConsts {
layout (offset = 64) float roughness;
layout (offset = 68) uint numSamples;
} consts;
const float PI = 3.1415926536;
// Based omn http://byteblacksmith.com/improvements-to-the-canonical-one-liner-glsl-rand-for-opengl-es-2-0/
float random(vec2 co)
{
float a = 12.9898;
float b = 78.233;
float c = 43758.5453;
float dt= dot(co.xy ,vec2(a,b));
float sn= mod(dt,3.14);
return fract(sin(sn) * c);
}
vec2 hammersley2d(uint i, uint N)
{
// Radical inverse based on http://holger.dammertz.org/stuff/notes_HammersleyOnHemisphere.html
uint bits = (i << 16u) | (i >> 16u);
bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
float rdi = float(bits) * 2.3283064365386963e-10;
return vec2(float(i) /float(N), rdi);
}
// Based on http://blog.selfshadow.com/publications/s2013-shading-course/karis/s2013_pbs_epic_slides.pdf
vec3 importanceSample_GGX(vec2 Xi, float roughness, vec3 normal)
{
// 基于粗糙度将二维点映射到半球
float alpha = roughness * roughness;
float phi = 2.0 * PI * Xi.x + random(normal.xz) * 0.1;
float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (alpha*alpha - 1.0) * Xi.y));
float sinTheta = sqrt(1.0 - cosTheta * cosTheta);
vec3 H = vec3(sinTheta * cos(phi), sinTheta * sin(phi), cosTheta);
// 切线空间
vec3 up = abs(normal.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
vec3 tangentX = normalize(cross(up, normal));
vec3 tangentY = normalize(cross(normal, tangentX));
// 转换到世界空间
return normalize(tangentX * H.x + tangentY * H.y + normal * H.z);
}
// Normal Distribution function
float D_GGX(float dotNH, float roughness)
{
float alpha = roughness * roughness;
float alpha2 = alpha * alpha;
float denom = dotNH * dotNH * (alpha2 - 1.0) + 1.0;
return (alpha2)/(PI * denom*denom);
}
vec3 prefilterEnvMap(vec3 R, float roughness)
{
vec3 N = R;
vec3 V = R;
vec3 color = vec3(0.0);
float totalWeight = 0.0;
float envMapDim = float(textureSize(samplerEnv, 0).s);
for(uint i = 0u; i < consts.numSamples; i++) {
vec2 Xi = hammersley2d(i, consts.numSamples);
vec3 H = importanceSample_GGX(Xi, roughness, N);// 将一个二维采样序列转换成三维空间中的采样方向
vec3 L = 2.0 * dot(V, H) * H - V; //L是反射
float dotNL = clamp(dot(N, L), 0.0, 1.0);
if(dotNL > 0.0) {
// Filtering based on https://placeholderart.wordpress.com/2015/07/28/implementation-notes-runtime-environment-map-filtering-for-image-based-lighting/
float dotNH = clamp(dot(N, H), 0.0, 1.0);
float dotVH = clamp(dot(V, H), 0.0, 1.0);
// 概率分布函数
float pdf = D_GGX(dotNH, roughness) * dotNH / (4.0 * dotVH) + 0.0001;
float omegaS = 1.0 / (float(consts.numSamples) * pdf);
// 所有立方体面之间的立体角为1像素
float omegaP = 4.0 * PI / (6.0 * envMapDim * envMapDim);
//通过+1来实现更好的效果
float mipLevel = roughness == 0.0 ? 0.0 : max(0.5 * log2(omegaS / omegaP) + 1.0, 0.0f);
color += textureLod(samplerEnv, L, mipLevel).rgb * dotNL; //反射的L对应的位置
totalWeight += dotNL;
}
}
return (color / totalWeight); //加权平均
}
void main()
{
vec3 N = normalize(inPos);
outColor = vec4(prefilterEnvMap(N, consts.roughness), 1.0);
}
