三角化算法-耳切法

徐行404
2,971 阅读3分钟

什么是三角化

将一个平面或曲面图形分割成若干个三角形的过程。

为什么需要三角化

为什么要进行三角剖分，它的研究动机在哪里，又是为了解决什么实际问题提出来的？ - 知乎 www.zhihu.com/question/25…

qastack.cn/gamedev/951…

三角化算法

三角化常见算法有两种：耳切法和德劳内三角化。

基础知识复习

叉乘

  • 计算公式

    给定向量

    a⃗=(x1,y1,z1),b⃗=(x2,y2,z2),\vec{\mathbf{a}} = (x_1, y_1, z_1),\\ \vec{\mathbf{b}} = (x_2, y_2, z_2),

    那么叉乘公式为，

    c⃗=(y1⋅z2−y2⋅z1)i⃗−(x1⋅z2−x2⋅z1)j⃗+(x1⋅y2−x2⋅y1)k⃗\vec{\mathbf{c}} = (y_1\cdot z_2 - y_2 \cdot z_1)\vec{\mathbf{i}} - (x_1 \cdot z_2 - x_2 \cdot z_1)\vec{\mathbf{j}} + (x_1 \cdot y_2 - x_2 \cdot y_1)\vec{\mathbf{k}}

    其中，

    i⃗={1,0,0},j⃗={0,1,0},k⃗={0,0,1}\vec{\mathbf{i}} = \{1, 0, 0\},\\ \vec{\mathbf{j}} = \{0, 1, 0\},\\ \vec{\mathbf{k}} = \{0, 0, 1\}

  • 右手法则

一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系是满足右手定则的，当右手的四指从a⃗\vec{\mathbf{a}}以不超过180度的转角转向b⃗\vec{\mathbf{b}}时，竖起的大拇指指向是c⃗\vec{\mathbf{c}}的方向。

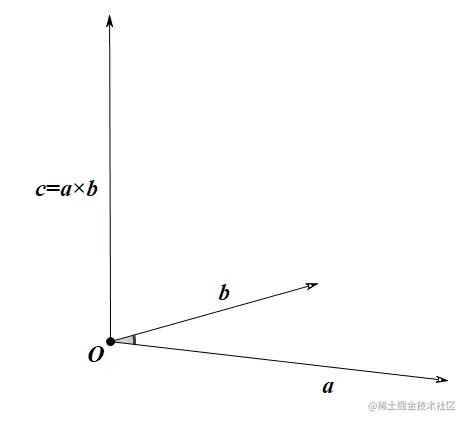
image.png

通过右手法则，其实可以发现叉乘的一个性质，可以用来判断向量a⃗\vec{\mathbf{a}}是在b⃗\vec{\mathbf{b}}的顺时针还是逆时针方向。具体如下：

  1. 如果a⃗×b⃗>0\vec{\mathbf{a}} \times \vec{\mathbf{b}} \gt 0， 则a⃗\vec{\mathbf{a}}在 b⃗\vec{\mathbf{b}}的顺时针方向；
  2. 如果a⃗×b⃗<0\vec{\mathbf{a}} \times \vec{\mathbf{b}} \lt 0， 则a⃗\vec{\mathbf{a}}在 b⃗\vec{\mathbf{b}}的逆时针方向。

判断一系列点是顺时针还是逆时针

（此处讨论前提是给定点列表要么是顺时针，要么是逆时针，不讨论既不是顺时针也不是逆时针的情况）。 方法：对每条边计算(x2−x1)(y2+y1)(x2-x1)(y2+y1)，相加看正负号，如果为正，则是顺时针。 证明： www.element84.com/blog/determ…

判断一个点是否在一个三角形内

设三角形<a,b,c>和点p。如果点p在三角形外，则在pa, pb, bc三条边中，必然有一条边同时在另外两条边的同一侧，如果在三角形内则没有这种情况。那么结合前文提到的叉乘性质，可以用如下方法来做判断： 假设给定三角形<a,b,c> (顶点按逆时针排列），以及一个点p，那么：

p  is inside the triangle  <a,b,c>  ⟺  pa⃗×pb⃗≥0  &  pb⃗×pc⃗≥0  &  pc⃗×pa⃗≥0p \;\text{is inside the triangle}\; <a,b,c> \iff \vec{\mathbf{pa}} \times \vec{\mathbf{pb}} \ge 0 \;\&\; \vec{\mathbf{pb}} \times \vec{\mathbf{pc}} \ge 0 \;\&\; \vec{\mathbf{pc}} \times \vec{\mathbf{pa}} \ge 0

耳切法（Ear Clipping）

一般情况

一个多边形的耳朵是指,一个多边形中连续的三个点, Vi0,Vi1,Vi2V_{i_0}, V_{i_1}, V_{i_2}，如果：

  1. Vi1V_{i_1}是个凸顶点（convex vertex)，且
  2. 线段Vi0Vi1V_{i_0}V_{i_1}在多边形内，且
  3. 多边形中没有其他顶点落在三角形<Vi0,Vi1,Vi2><V_{i_0}, V_{i_1}, V_{i_2}>内，

则称Vi0,Vi1,Vi2V_{i_0}, V_{i_1}, V_{i_2}是该多边形的一个耳朵，Vi1V_{i_1}叫做耳尖。

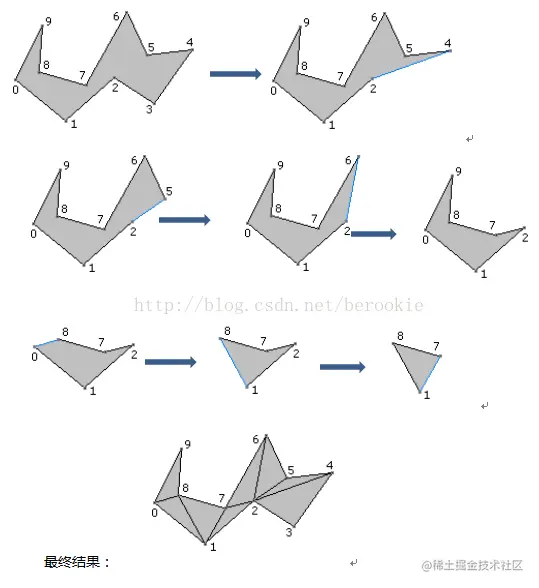
对于一个三角形而言，包含一个耳朵。对于一个边数大于三的多边形而言，至少有两个不重叠的耳朵【2】。基于此，就有了耳切法。 既然对于多边形（边大于4）而言，至少有两个耳朵，那么可以不断地迭代找到其中一个耳朵，然后移除耳朵的耳尖，再继续迭代查找，直到只剩下一个耳朵（三个点）。

举个例子。

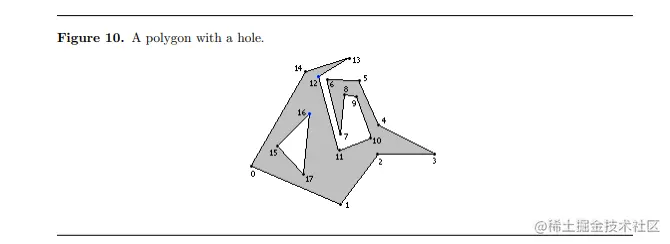
image.png

包含一个洞的简单多边形

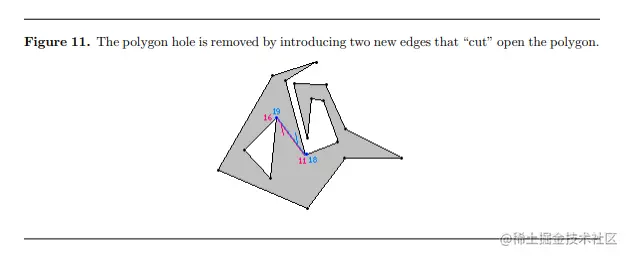
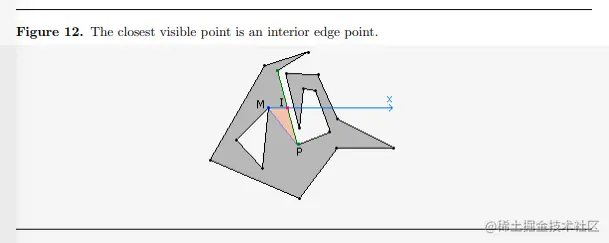
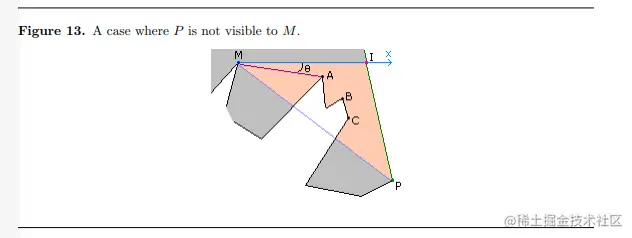
image.png

image.png

查找相互可见的顶点

image.png image.png 算法总结如下:

  1. 寻找内部多边形x周最大值的顶点M
  2. 沿X轴正方向，寻找最近的相交边<Vi,Vi1><V_i,V_{i_1}>,让其焦点设置为I，构成X轴方向对M的最近可见点
  3. 如果I是一个外部顶点，则M和I相互可见，算法执行结束
  4. 如果I只是边上的一个点，寻找端点中x值中大的一个，设置为P
  5. 寻找位于P内的其他外多边形的可连接顶点。如果所有的顶点都在<M,I,P><M,I,P>之外，则M与P相互可见，结束算法；
  6. 如果有至少一个点位于三角形<M,I,P>内部，则寻找其中的一个顶点，计算其与x轴(1,0)的夹角，夹角最小的顶点R与M构成相互可见边，算法结束
  7. 在这个算法中，有可能有多个顶点同事具有最小的角度，这种情况下，寻找距离M最近的一个点即可

嵌套洞的多边形

对于层层嵌套的多边形，可以构造一棵树，树的根节点是最外层的多边形，其孩子节点是第二层的多边形。依次类推。树构造完成后，用bfs遍历处理即可。

引用

【1】www.geometrictools.com/Documentati…

【2】G.H. Meisters, Polygons have ears, Amer. Math. Monthly, vol. 82, pp. 648-651, 1975

avatar
文章
阅读
粉丝