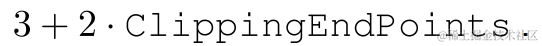Halcon 算子 fit_circle_contour_xld

作用：用圆近似XLD轮廓；

参数翻译（对应以上参数顺序）：

输入轮廓、

圆拟合算法（详细算法解释如下）、

用于计算的最大轮廓点数（MaxNumPoints >= 3，-1是所有点）、

闭合轮廓端点之间的最大距离（轮廓两头的距离MaxClosureDist >= 0.0）、

拟合过程忽略的点（轮廓首尾ClippingEndPoints >= 0）、

稳健加权拟合的最大迭代次数（Iterations >= 0）、

用于剔除异常值的剪切因子（ClippingFactor > 0）一般情况下:Huber算法设置为 1.0、Tukey算法设置为 2.0、

输出圆心的行坐标、输出圆心坐标的列坐标、输出圆的半径、输出起始点的角度、输出结束点的角度、输出沿边界的点序；

 

圆拟合算法（Algorithm参数）：

代数方法：

（1）、'algebraic'  这种方法使轮廓点与所得圆之间的代数距离最小；

（2）、'ahuber'     类似于“代数方法（algebraic）”,在此基础上，采用Huber方法对等高线点进行加权，以减小异常值的影响；

（3）、'atukey'      类似于“代数方法（algebraic）”，在此基础上，采用Tukey算法对轮廓点进行加权，忽略离群点;

几何方法：

（4）、'geometric'  这种方法最小化轮廓点和结果圆之间的几何距离,这种算法在距离统计上是最优的，但需要更多的计算时间，如果轮廓点被噪声严重影响，建议使用这个选项；

（5）、'geohuber'  类似于“几何方法（geometric）”,在此基础上，采用Huber方法对等高线点进行加权，以减小异常值的影响;

（6）、'geotukey'  类似于“几何方法（geometric）”,在此基础上，采用Tukey算法对轮廓点进行加权，忽略离群点；

 

描述：

（1）、fit_circle_contour_xld用圆近似XLD轮廓，它不执行对输入轮廓的分割，因此，我们必须确保每条等高线都只对应一个圆。使用如上算法，操作符为每个轮廓返回中心(行、列)坐标和半径；对于“*huber”和“*tukey”，在没有近似圆异常值的影响下，它们采用稳健的误差统计来估计轮廓点距离的标准偏差；

（2）、参数ClippingFactor(标准偏差的比例因子)控制了异常值的数量：为ClippingFactor选择的值越小，检测到的离群值就越多；

（3）、在Tukey算法中离群值是会被剔除的，而在Huber算法中，离群值只被阻尼，更准确地说，它们是线性加权的；在没有任何鲁棒加权的情况下，优化时采用距离的平方作为误差值，即最小二乘公式，在实践中，建议采用Tukey方法。

（4）、参数Iterations指定算法“algebra”、“ahuber”和“atukey”的迭代次数，对于算法'geometric'， 'geohuber'和'geotukey'，这个参数会被忽略。如果迭代次数设置为0，则算法不会对拟合圆进行迭代改进，但是会检查最初的猜测是否已经足够接近，这也取决于对异常值的处理方法选择。

（5）、为了减少计算量，可以将圆的拟合限制在轮廓点的子集内；如果MaxNumPoints的值不是-1，只有达到MaxNumPoints设置的最大点数均匀分布在轮廓上才使用。

（6）、对于圆弧，选择圆上最接近原始轮廓起始点和结束点的点作为起始点和结束点，与x轴对应的角度在StartPhi和EndPhi中返回；

（7）、XLD轮廓上，起点和终点之间的距离小于或等于MaxClosureDist设置的值的轮廓被认为是闭合的，这种情况下，用圆代替圆弧来近似它们；

由在预处理过程中可能导致轮廓的起始点和结束点出现问题，因此，可以从圆的拟合中排除轮廓开始点和结束点（设置ClippingEndPoints的值 ），虽然如此，它们仍然被用于StartPhi和EndPhi的测定；

 

注意：

         拟合圆所需轮廓点的最小数目是三个，因此，要求等高线点的个数至少要符合以下公式计算的点数：