阅读论文:2017 Real-Time Bidding by Reinforcement Learning in Display Advertising
图片和数据出自原文,为了表示方便,公式编号和文中保持一致
1 背景
将强化学习应用于展示广告场景下的实时竞价,提出了RLB(reinforcement learning to bid)算法,主要工作为
- 建立马尔可夫决策过程(MDP)框架,学习最优竞价策略
- 为了处理现实世界拍卖数量和活动预算的可伸缩性问题,利用神经网络模型来近似价值函数
- 除了直接泛化神经网络值函数外,文章提出了一种新颖的粗细集分割模型(coarse-tofine episode segmentation model)和状态映射模型(state mapping models),以克服大规模状态泛化问题
2 方法
2.1 问题定义
可以认为在展示广告中,出价是一个episodic process,对于每个episode有T个拍卖过程,每次拍卖都用高维特征向量x表示。在开始时,agent初始化预算为B,广告目标是获得尽可能多的点击。agent主要考虑3条信息。在episode中,agent根据t,b和x进行出价。
- 剩余的竞价t∈{0,...,T}
- 未用的预算b∈{0,...,B}
- 拍卖的特征x
在拍卖次数为t时,记竞价中market price的概率密度函数为m(δ,x),如果以价格δ赢得拍卖,剩余的预算更新为b−δ,在这种情况下,agent可以观察到用户的反馈(比如是否点击)和市场价格;如果竞价失败,agent没有获得任何信息。记预测的CTR(pCTR)为θ(x),作为优化的目标。 一次拍卖结束后,剩余的拍卖次数变为t-1,episode结束时,预算和拍卖次数被重置。
马尔可夫决策过程(MDP)提供了一个广泛用于建模agent-environment交互的框架,文章使用符号如下所示
| Notation | Description |
|---|
| x | 表示一次竞价的特征向量 |
| X | 整个特征向量空间 |
| px(x) | x的概率密度函数 |
| θ(x) | x在赢得拍卖的情况下,估计的点击率 |
| m(δ,x) | 给定δ和x的情况下,胜出的概率密度函数 |
| m(δ) | 给定δ的情况下,胜出的概率密度函数 |
| V(t,b,x) | 在状态为(t,b,x)情况下,期望的总回报(取最优的策略) |
| V(t,b) | 在状态为(t,b)情况下,期望的总回报(取最优的策略) |
| a(t,b,x) | 在状态为(t,b,x)情况下,最优的action |
MDP可以表示为(S,{As},{Pss′a},{Rss′a}),其中S和A表示为可能的状态和动作的集合,Pss′a为通过动作a,从状态s转移到状态s′的概率,奖励函数为r(a,s,s′)。
可以认为xt符合px(x)的独立条件分布,整个状态空间为S={0,...,T}×{0,...,B}×X。t=0即为episode的结束,(t,b,xt)是可行的动作集合为A(t,b,xt)。竞价有两种转移状态
- 竞价成功:在(t,b,xt)且t>0时,如果出价为a(δ∈{0,...,a},即a大于market price),以px(xt−1)m(δ,xt)的概率跳转到状态(t−1,b−δ,xt−1),并获得奖励θ(xt)
- 竞价失败:agent以px(xt−1)∑δ=a+1∞m(δ,xt)的概率转移到(t−1,b,xt−1)。由于拍卖程序的原因,其他所有的过渡都是不可能的
因此转移概率和奖励函数如下,记为公式(1)
μ(a,(t,b,xt),(t−1,b−δ,xt−1))=px(xt−1)m(δ,xt)
μ(a,(t,b,xt),(t−1,b,xt−1))=px(xt−1)∑δ=a+1∞m(δ,xt)
r(a,(t,b,xt),(t−1,b−δ,xt−1))=θ(xt)
r(a,(t,b,xt),(t−1,b,xt−1))=0
因此确定性策略π指从状态s∈X映射到action a∈As,比如a=π(s),对于竞价过程中的出价。在策略π下,有价值函数Vπ(s),满足贝尔曼等式(Bellman equation),并且折扣系数γ=1(因为在场景中,总点击次数是优化目标,而与点击时间无关),有如下关系
Vπ(s)=∑s′∈Sμ(π(s),s,s′)(r(π(s),s,s′)+Vπ(s′))(2)
最优的价值函数为V∗(s)=maxπVπ(s),最优的策略为
π∗(s)=a∈Asargmax{∑s′∈Sμ(a,s,s′)(r(a,s,s′)+V∗(s′))}(3)
最优策略π∗(s)为求解的目标,为了表示方便,使用V(s)表示V∗(s)。
上述建模为model-based的解决方案,用到了px(x)和m(δ,x)
2.2 问题求解
等式(3)可以使用动态规划方法解决。 根据定义,具有最优值函数V(t,b,x),其中(t,b,x)表示状态。同时,考虑没有观察到特征向量x的情况,所以另一个最优值函数是V(t,b),有如下关系V(t,b)=∫Xpx(x)V(t,b,x)dx。
根据定义V(0,b,x)=V(0,b)=0,表示没有剩余的拍卖。根据等式(1)中转移概率和奖励,有如下关系
V(t,b,x)==0≤a≤bmax{δ=0∑a∫Xm(δ,x)px(xt−1)(θ(x)+V(t−1,b−δ,xt−1))dxt−1+δ=a+1∑∞∫Xm(δ,x)px(xt−1)V(t−1,b,xt−1)dxt−1}0≤a≤bmax{δ=0∑am(δ,x)(θ(x)+V(t−1,b−δ))+δ=a+1∑∞m(δ,x)V(t−1,b)}(4)
其中等式右边第一个求和表示竞价成功,第二个求和表示竞价失败。在(t,b,x)时,最优出价为
a(t,b,x)=0≤a≤bargmax{∑δ=0am(δ,x)(θ(x)+V(t−1,b−δ))+∑δ=a+1∞m(δ,x)V(t−1,b)}(5)
其中最优竞价action a(t,b,x)包含三个因子:m(δ,x)、θ(x)和V(t−1,⋅)。V(t,b)是通过边缘化x得到的
V(t,b)=∫Xpx(x)max0≤a≤b{∑δ=0am(δ,x)(θ(x)+V(t−1,b−δ))
+∑δ=a+1∞m(δ,x)V(t−1,b)}dx
=max0≤a≤b{∑δ=0a∫Xpx(x)m(δ,x)θ(x)dx+∑δ=0aV(t−1,b−δ)
∫Xpx(x)m(δ,x)dx+V(t−1,b)∑δ=a+1∞∫Xpx(x)m(δ,x)dx}
=max0≤a≤b{∑δ=0a∫Xpx(x)m(δ,x)θ(x)dx+
∑δ=0am(δ)V(t−1,b−δ)+V(t−1,b)∑δ=a+1∞m(δ)}(6)
为了解决公式(6)中的积分问题,使用近似m(δ,x)≈m(δ),因此得到
∫Xpx(x)m(δ,x)θ(x)dx≈m(δ)∫Xpx(x)θ(x)dx=m(δ)θavg(7)
其中θavg为pCTRθ的期望值,可以通过历史的数据进行计算,将式(7)带入到式(6)中,可以得到如下结果
V(t,b)≈max0≤a≤b{∑δ=0am(δ)θavg+∑δ=0am(δ)V(t−1,b−δ)+
∑δ=a+1∞m(δ)V(t−1,b)}(8)
因为∑δ=0∞m(δ,x)=1,公式(5)可以写作下面形式
a(t,b,x)=0≤a≤bargmax{∑δ=0am(δ,x)(θ(x)+V(t−1,b−δ))−
∑δ=0am(δ,x)V(t−1,b)}
=0≤a≤bargmax{∑δ=0am(δ,x)(θ(x)+V(t−1,b−δ)−V(t−1,b))}
≡0≤a≤bargmax{∑δ=0am(δ,x)g(δ)}(9)
记g(δ)=θ(x)+V(t−1,b−δ)−V(t−1,b),有如下结论
- V(t−1,b)随着b增加而下降
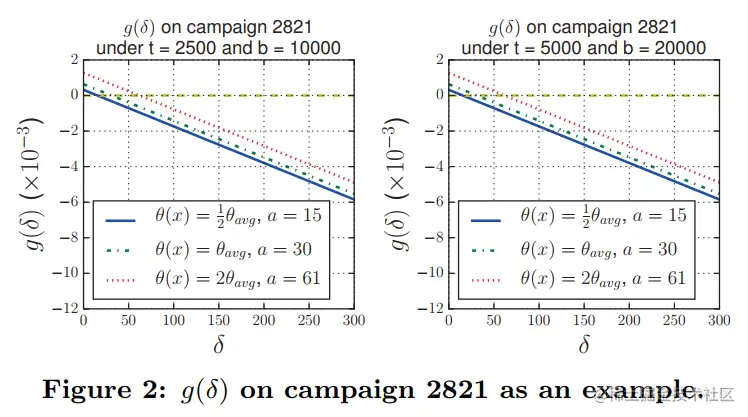
- g(δ)随着δ增加而下降
- g(0)=θ(x)≥0,m(δ,x)≥0
- 当0≤b′≤b,有g(b′)≥g(b)≥0,因此有m(δ,x)g(δ)≥0,其中0≤δ≤b,a(t,b,x)=b
- 如果g(b)<0,必定存在整数A,0≤A<b,g(A)≥0,g(A+1)<0。因此在δ<A时m(δ,x)g(δ)≥0,δ≤A时m(δ,x)g(δ)<0
出价有如下情况
a(t,b,x)={bAg(A)≥0 and g(A+1)<0 if g(b)≥0 if g(b)<0(10)
下图显示了g(δ)在数据集中的分布,在文中设置市场价格的上界δmax。
RLB(reinforcement learning to bid)算法如下

Discussion on Derived Policy
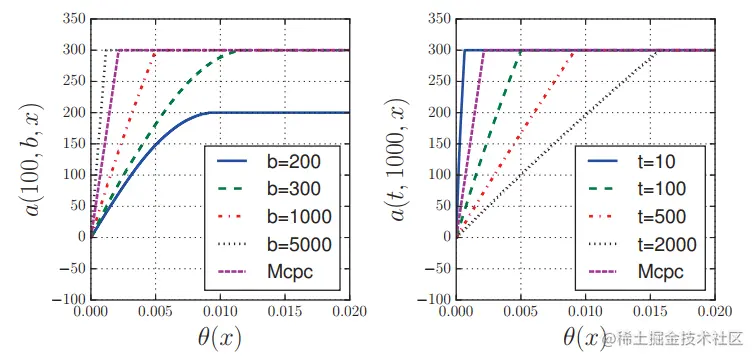
RLB根据t和b调节出价策略,如下图所示,当b很大时,出价形式为线性,当b很小时(b<300),出价形式为非线性。
Discussion on the Approximation ofV(t,b)
此处略,感觉不是很重要
2.3 处理大规模问题
算法1给出了求解最优策略的方式,但是在实际应用中存在一定的问题。在更新V(t,b)的过程中,存在两层的循环,算法时间复杂度为O(TB),空间复杂度为O(TB)。在实际应用中,T和B很大,因此计算V(t,b)费时且无法存储。
由于计算资源有限,可能无法完成整个值函数的更新。为此,提出了小数据尺度上的参数化模型,即{0,⋅⋅⋅,T0}×{0,⋅⋅⋅,B0},并推广到大数据尺度上的{0,⋅⋅⋅,T}×{0,⋅⋅⋅,B}。
对于大多数的V(t,b)会远远大于θavg,比如预算b足够大,则v(t,b)可以认为是t×θavg。因此如果直接优化V(t,b)会比较困难(意思就是V(t,b)的变化相对θavg很大)。
上述问题的解决方法为直接优化D(t,b)=V(t,b+1)−V(t,b),V(t,b)的计算如下
V(t−1,b−δ)−V(t−1,b)=−∑δ′=1δD(t−1,b−δ′)
D(t,b)的形式如下,固定t时,把D(t,b)记作Dt(b);固定b时,把D(t,b)记作Db(t)。性质有
- 在b很小时,Dt(b)波动很大
- Dt(b)随着b值增加减小
- Db(t)随着t值增加增大
- Db(t)和Dt(b)都是非线性形式的函数
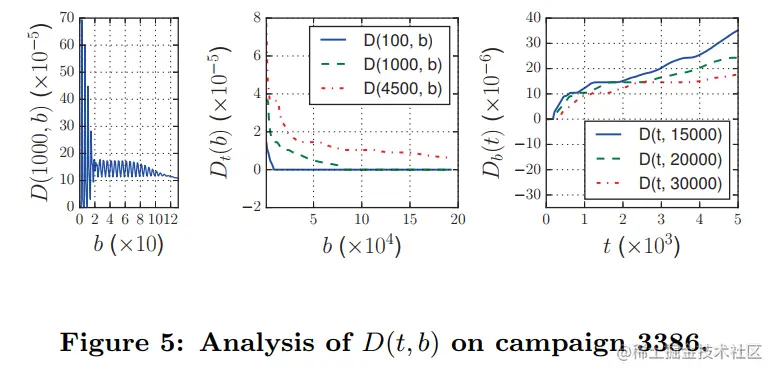
使用神经网络来拟合D(t,b),输入为t和b,输出为D(t,b),神经网络记作NN(t,b)。
Coarse-to-fine Episode Segmentation Model
由于神经网络不能保证良好的泛化能力,而且可能会发生过拟合,为了避免直接建模D(t,b)或V(t,b),文中探索了映射未见状态的可行性。即将状态t>T0和B>B0映射到t≤T0和B≤B0。与budget pacing类似,有第一种简单的隐式映射方法,可以将大episode分成几个长度为T0的小episode,在每个大episode中,将剩余的预算分配给剩余的小episode。如果agent不把预算花在小episode上,那么在大episode的其他小episode上就会有更多的预算。
State Mapping Models
由于Dt(b)随着b值增加减小,Db(t)随着t值增加增大,当t和b很大时,应该存在点{(t′,b′)},满足D(t′,b′)=D(t,b),即D(t,b)存在状态映射。a(t,b,x)随着t增加减小,随着b增加增加,因此a(t,b,x)也存在类似的映射。
从实际竞价的角度来看,当剩余拍卖数量较多且预算情况类似时,给定相同的投标请求,agent应给出相似的竞价(见图2)。文中考虑一个简单的情况,b/t表示预算条件。然后有两种线性映射形式:
- 当t>T0时,映射a(t,b,x)到a(T0,tb×T0,x)
- 当t>T0时,映射D(t,b)到D(T0,tb×T0)
记Dev(t,T0,b)=∣D(t,b)−D(T0,tb×T0)∣,如下图表示,上述映射是合理的
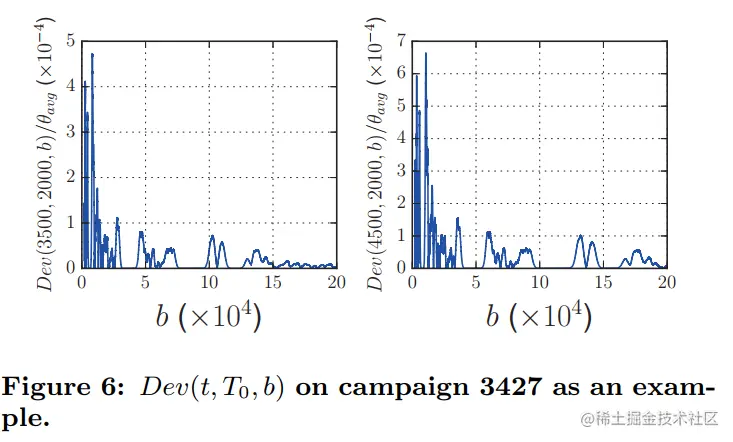
3 实验
3.1 实验设置
实验数据集介绍可见原文,评价指标为点击量,同时看CPM、eCPC等,其他实验设置参见原文。
比较方法有(有的方法需要看原文才知道具体实现,此处只简单记录)
- SS-MDP:在给出投标价格时,考虑投标情况,但忽略投标请求的特征向量。
- Mcpc:出价为aMcpc(t,b,x)=CPC×θ(x)
- Lin:线性的出价策略,根据pCTR进行出价,aLIN(t,b,x)=b0θavgθ(x)
- RLB:本文算法1提出的方法,适用于小数据规模的竞价
- RLB-NN:使用NN(t,b)来近似D(t,b)
- RLB-NN-Seg:对预算那进行划分,Bs=Br/Nr,其中Br为剩余预算,Nr为剩余的小episode,使用RLB-NN进行竞价,这种策略符合coarse-to-fine episode segmentation model。
- RLB-NN-MapD:使用NN(t,b)来近似D(t,b),并且当t>T0时,映射D(t,b)=NN(T0,tb×T0)
- RLB-NN-MapA:使用NN(t,b)来近似D(t,b),并且当t>T0时,映射a(t,b,x)到a(T0,tb×T0,x)
3.2 实验结果
Small-Scale Evaluation
在T=1000和不同预算下,实验结果如下图所示
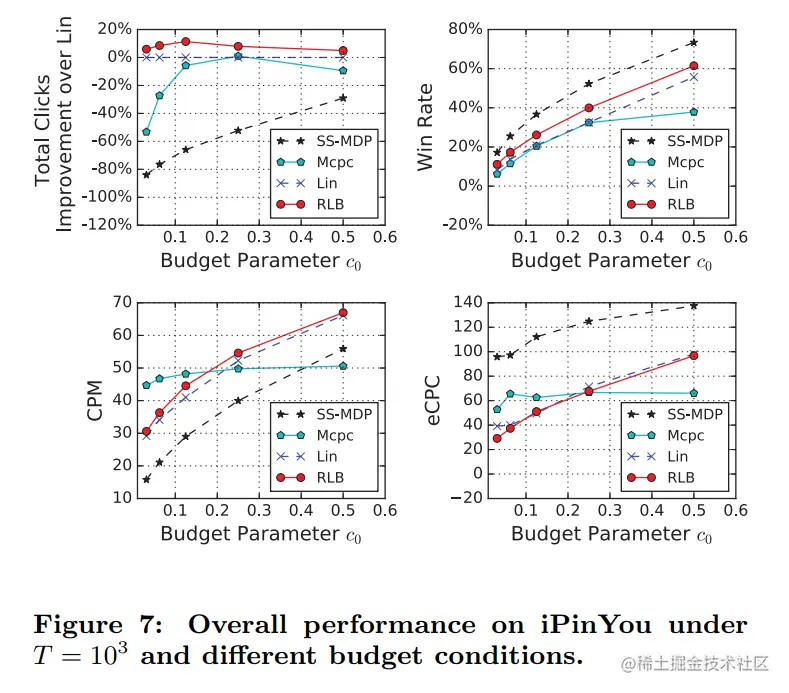
结论有
- 提出的模型RLB在各种预算条件下都表现最佳,验证了所提算法对获得点击量优化的有效性。
- LIN表现次之,是业界广泛使用的一种投标策略
- 与RLB和Lin相比,Mcpc不会在预算条件变化时调整策略。因此,当c0>1/4时,它的性能非常好,但在非常有限的预算条件下表现不佳
- SS-MDP的性能最差,因为它不知道每个投标请求的特征信息,这说明了RTB显示广告的优势
比较win rate,结论有
- 在各种预算条件下,SS-MDP始终保持最高的胜率。其原因是SS-MDP对每个投标请求的考虑是均等的,因此其优化目标与印象数是等价的
- 与CPM和eCPC相比,Lin和RLB非常接近。相对于Lin, RLB可以通过CPM和eCPC产生更高的点击量,因为RLB 根据市场情况有效地花费了预算,而Lin没有意识到这一点
在不同预算下实验结果如表所示
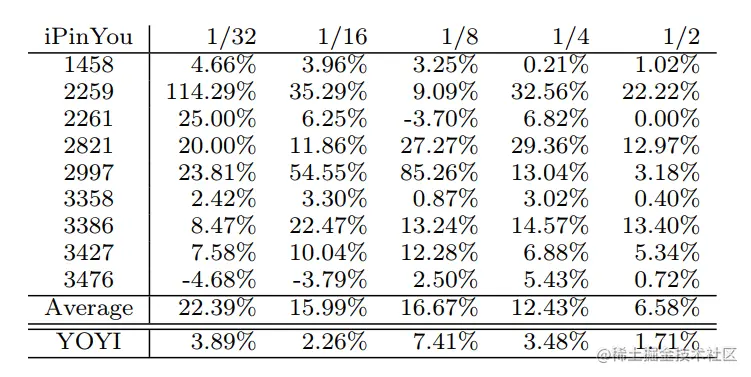
结论有
取预算为1/5,不同T下实验结果如下图所示
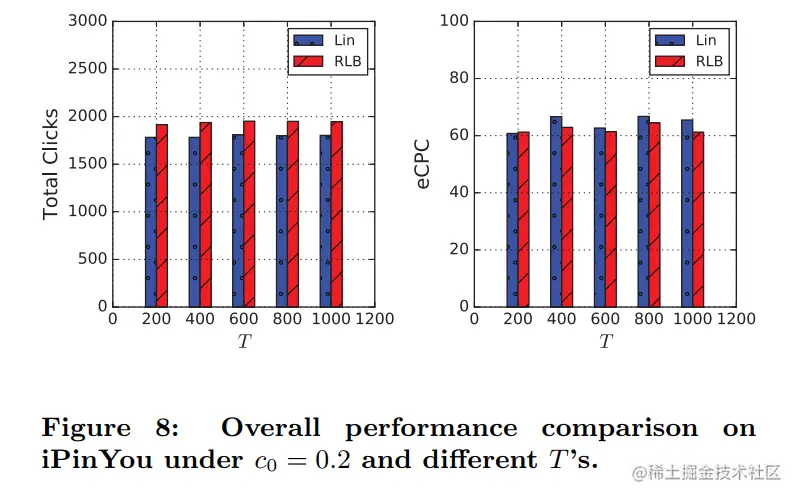
结论如下
- 与Lin相比,RLB在eCPC相似的情况下可以获得更多的点击量
下表比较了CTR估计结果和竞价的结果,当CTR估计较差时(AUC < 70%),与Mcpc和Lin相比,SS-MDP在点击上是相当好的。相比之下,当CTR估计器的性能提高时,其他使用CTR估计器的方法比SS-MDP获得更多的点击量。
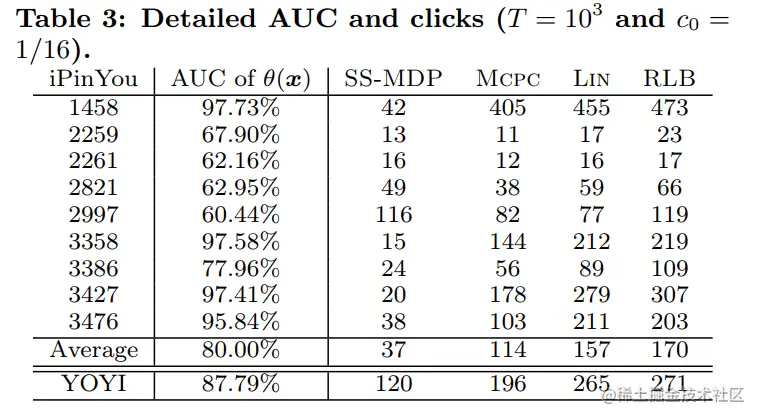
Large-Scale Evaluation
先设置为T0=10,000,B0=CPMtrain×10−3×T0×1/2,运行算法1。接着设置为T=100,000,B=CPMtrain×10−3×T0×c0,使用神经网络训练得到NN(t,b)。
下表显示了神经网络在不同数据集上的结果,可以看到RMSE相对θavg小,即使用神经网络在(t,b)∈{0,...,T0}×{0,...,B0}近似时效果较好。

在T=100,000是,实验结果如下
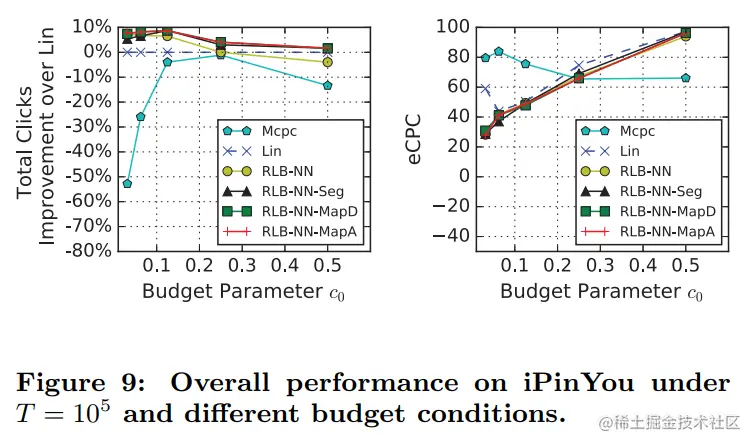
结论有
- Mcpc的性能与在小规模情况下观察到的类似
- 在总点击量方面,RLB-NN在c0 = 1/32、1/16、1/8下表现优于Lin,在c0 = 1/2下表现不如Lin,表明神经网络的泛化能力仅在小尺度下是令人满意的,在大尺度下RLB-NN效果不好
- 与RLB-NN相比,RLBNN-Seg、RLB-NN-MapD和RLB-NN-MapA三种复杂算法在各种预算条件下都具有更强的鲁棒性,优于Lin算法。它们不依赖于近似模型的泛化能力,因此性能更稳定。结果表明,它们是大规模问题的有效解决方案
- 在eCPC算法中,除Mcpc之外的所有模型都非常接近,从而使所提出的RLB算法更符合实际
ONLINE DEPLOYMENT AND A/B TEST
线上实验结果如下图所示
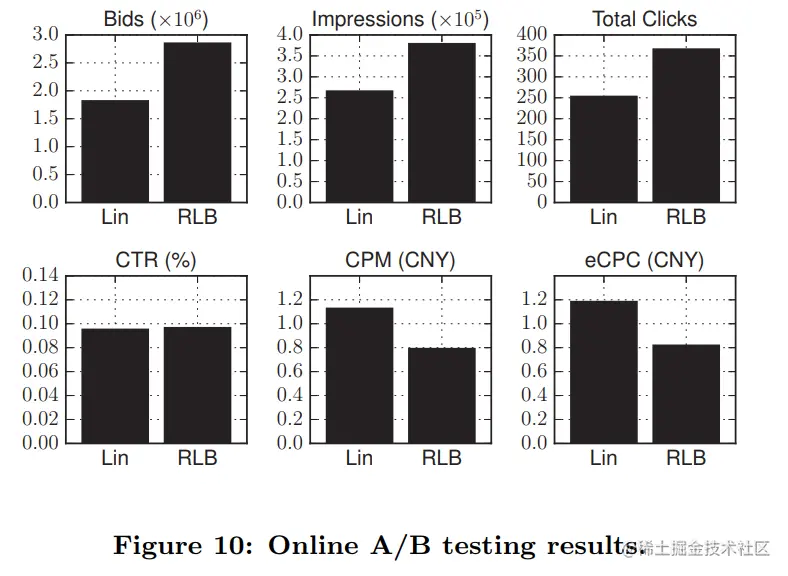
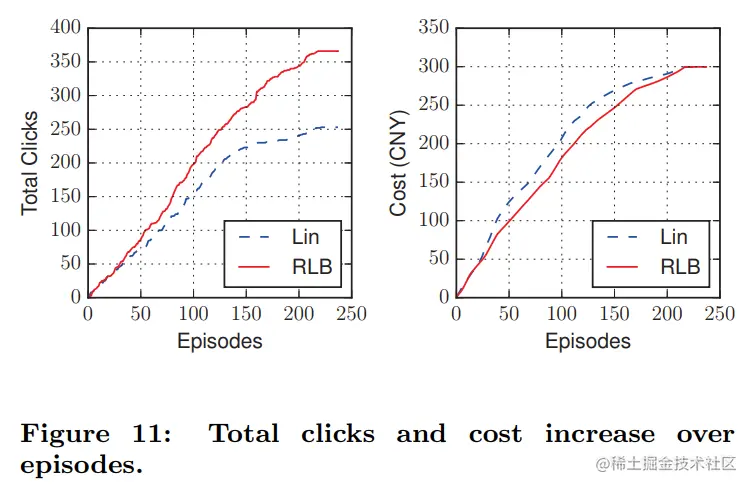
结论有
- 在相同的成本下,RLB的eCPC比Lin更低,从而获得了更多的总点击量,RLB更加有效率
- RLB提供了比Lin更好的计划:获得的点击量和花费的预算在不同时间内平均增长
- 通过更好的规划,RLB获得的CPM比Lin更低,产生了更多的出价和赢得更多的曝光
- 在低成本的情况下,RLB的CPM较低,达到了一个较好的结果,CTR与Lin相比,性能更优越
4 总结
文中的公式较多,看过强化学习后才能比较好理解文中推导。全文推导十分清晰,建议仔细阅读原文(公式太多笔记有点乱)。
本文正在参与「掘金 2021 春招闯关活动」, 点击查看 活动详情