论文阅读 (011): Optimal Real-Time Bidding for Display Advertising | 技术点评

Shentao
1,499 阅读9分钟

阅读论文：2014 Optimal Real-Time Bidding for Display Advertising

该论文是Weinan Zhang在2016年发表的Bid-aware Gradient Descent for Unbiased Learning with Censored Data in Display Advertising之前的工作，两者有较大的关联

1 背景

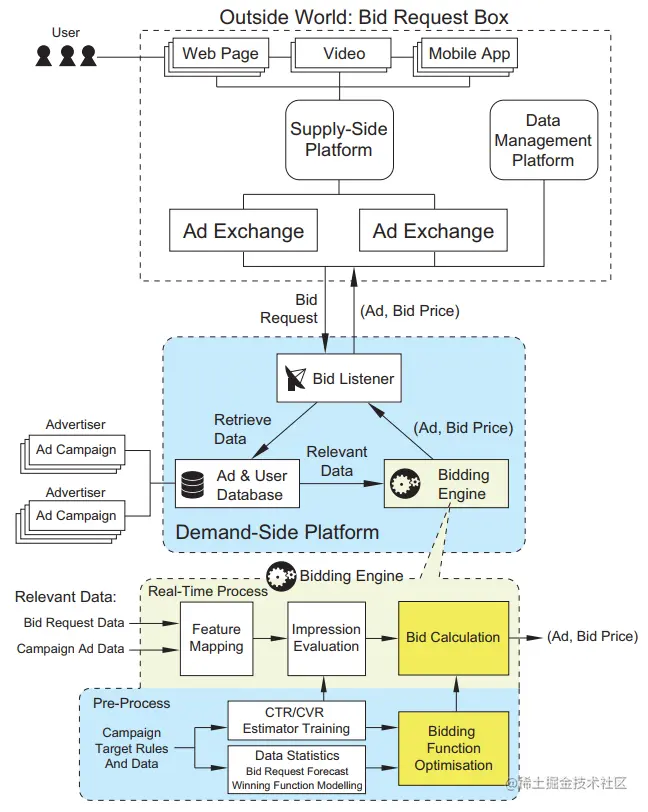
上图展示了DSP在实时竞价系统中的角色，在系统中，一个用户访问页面时，产生了一次曝光，SSP向DSP发送竞价的请求；接着DSP会计算对本次曝光的出价，并且返回给Ad Exchange；最后胜者会收到通知，将其广告进行曝光。系统中Bidding Engine给出实时的竞价。

实时竞价的意义在于

  • 允许每次展示交易可扩展包括剩余部分在内的大量可用广告库存（可以做到精细化出价和预算控制）
  • 广告购买时着眼于用户数据而非上下文数据（受众定向更加准确）

文章的贡献有

  • 提出了一种新颖的优化框架，以便在实时出价展示广告中找到最佳出价策略
  • 根据数据构建的拍卖胜出函数，从框架中得出的最佳出价函数，并且该出价函数是对每次曝光KPI( Key Performance Indicator)是凸的

2 最优实时竞价

2.1 问题定义

对文中使用变量做定义，定义如下

符号描述
x\boldsymbol{x}广告请求，使用特征来表示（从广告本身中提取的特征、与展示相关的特征）
px(x)p_x(\boldsymbol{x})x的概率分布，这里应该指的是在请求数据中x的分布
θ(x)\theta(\boldsymbol{x})预测广告胜出时的KPI，常用的有：CTR，CVR
pθ(θ)p_{\theta}(\theta) KPI θ\theta 的概率密度函数
B广告预算
NTN_T在预算的有效期内估计的广告竞价请求数量
b(θ(x),x)b (\theta (\boldsymbol{x}), \boldsymbol{x})竞价函数b，进行简化：b(θ(x),x)≡b(θ(x))b(\theta(\boldsymbol{x}), \boldsymbol{x}) \equiv b(\theta(\boldsymbol{x}))
w(b(θ(x)),x)w(b(\theta(\boldsymbol{x})), \boldsymbol{x})在给定出价b(θ(x))b(\theta(\boldsymbol{x}))时的胜出概率，同样进行简化：w(b(θ(x)),x)≡w(b(θ(x)))w(b(\theta(\boldsymbol{x})), \boldsymbol{x}) \equiv w(b(\theta(\boldsymbol{x})))

问题是设计一个最优的投标策略，在预算限制的条件下最大化KPI。文章将点击次数作为优化的目标，优化函数如下

b()ORTB=arg⁡max⁡ b() NT∫xθ(x)w(b(θ(x),x),x)px(x)dx subject to NT∫xb(θ(x),x)w(b(θ(x),x),x)px(x)dx≤B\begin{aligned} b()_{\mathrm{ORTB}} & = \underset{\text { b() }}{\arg \max } N_{T} \int_{\boldsymbol{x}} \theta(\boldsymbol{x}) w(b(\theta(\boldsymbol{x}), \boldsymbol{x}), \boldsymbol{x}) p_{x}(\boldsymbol{x}) d \boldsymbol{x} \\ & \text { subject to } N_{T} \int_{\boldsymbol{x}} b(\theta(\boldsymbol{x}), \boldsymbol{x}) w(b(\theta(\boldsymbol{x}), \boldsymbol{x}), \boldsymbol{x}) p_{x}(\boldsymbol{x}) d \boldsymbol{x} \leq B \end{aligned}

因为将优化目标表示为了积分形式，所以用到了pθ(θ)p_{\theta}(\theta) ，其中θ(x)\theta(\boldsymbol{x})和w(b(θ(x)),x)w(b(\theta(\boldsymbol{x})), \boldsymbol{x})相乘表示为对一次竞价的点击概率，优化中约束为在预算有效期内胜出后出价不能超过B。

在对b(θ(x),x)b (\theta (\boldsymbol{x}), \boldsymbol{x})和w(b(θ(x)),x)w(b(\theta(\boldsymbol{x})), \boldsymbol{x})做适当的简化后，优化问题如下

b()ORTB=arg⁡max⁡b()NT∫xθ(x)w(b(θ(x)))px(x)dx subject to NT∫xb(θ(x))w(b(θ(x)))px(x)dx≤B\begin{aligned} b()_{\mathrm{ORTB}}=\underset{b()}{\arg \max } & N_{T} \int_{\boldsymbol{x}} \theta(\boldsymbol{x}) w(b(\theta(\boldsymbol{x}))) p_{x}(\boldsymbol{x}) d \boldsymbol{x} \\ \text { subject to } & N_{T} \int_{\boldsymbol{x}} b(\theta(\boldsymbol{x})) w(b(\theta(\boldsymbol{x}))) p_{x}(\boldsymbol{x}) d \boldsymbol{x} \leq B \end{aligned}

使用等式pθ(θ(x))=px(x)∥∇θ(x)∥p_{\theta}(\theta(\boldsymbol{x}))=\frac{p_{x}(\boldsymbol{x})}{\|\nabla \theta(\boldsymbol{x})\|}对上述式子进行替换，将关于x的积分形式表示为关于θ\theta的积分形式，优化问题如下

b()ORTB=arg⁡max⁡b()NT∫θθw(b(θ))pθ(θ)dθ subject to NT∫θb(θ)w(b(θ))pθ(θ)dθ≤B\begin{aligned} b()_{\mathrm{ORTB}} &=\underset{b()}{\arg \max } N_{T} \int_{\theta} \theta w(b(\theta)) p_{\theta}(\theta) d \theta \\ & \text { subject to } N_{T} \int_{\theta} b(\theta) w(b(\theta)) p_{\theta}(\theta) d \theta \leq B \end{aligned}

2.2 问题求解

2.1中优化问题的拉格朗日形式如下

L(b(θ),λ)=∫θθw(b(θ))pθ(θ)dθ−λ∫θb(θ)w(b(θ))pθ(θ)dθ+λBNT\mathcal{L}(b(\theta), \lambda)= \int_{\theta} \theta w(b(\theta)) p_{\theta}(\theta) d \theta - \lambda \int_{\theta} b(\theta) w(b(\theta)) p_{\theta}(\theta) d \theta+\frac{\lambda B}{N_{T}}

根据变分法，b(θ)b(\theta)的欧拉-拉格朗日条件为

θpθ(θ)∂w(b(θ))∂b(θ)−λpθ(θ)[w(b(θ))+b(θ)∂w(b(θ))∂b(θ)]=0\theta p_{\theta}(\theta) \frac{\partial w(b(\theta))}{\partial b(\theta)}-\lambda p_{\theta}(\theta)\left[w(b(\theta))+b(\theta) \frac{\partial w(b(\theta))}{\partial b(\theta)}\right]=0

λw(b(θ))=[θ−λb(θ)]∂w(b(θ))∂b(θ)\lambda w(b(\theta))=[\theta-\lambda b(\theta)] \frac{\partial w(b(\theta))}{\partial b(\theta)}

其中b(θ)b(\theta)和概率分布pθ(θ)p_{\theta}(\theta)无关，仅取决于w(b(θ))w(b(\theta))。

不同的获胜函数(winning function)会产生不同的最优出价函数。这里我们给出了两个典型的、拟合真实世界数据曲线的获胜函数，并推导出各出价函数的最优出价函数形式。

Winning & Bidding Function 1

在出价低的时候，提高出价会较大提升获胜概率，在出价高的时候，提高出价对获胜概率的提升较小，因此定义获胜函数

w(b(θ))=b(θ)c+b(θ)w(b(\theta))=\frac{b(\theta)}{c+b(\theta)}

其中c为常数，对于不同的c，获胜概率如Figure 2(a)所示。

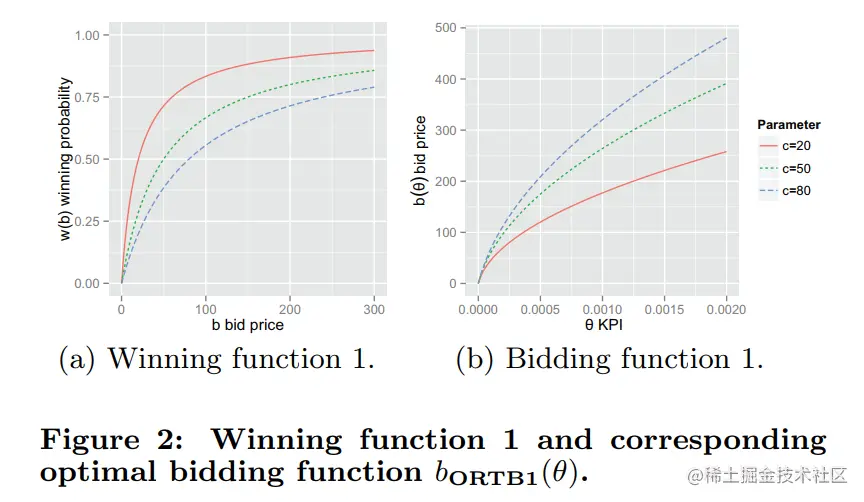
把获胜函数带入b(θ)b(\theta)的欧拉-拉格朗日条件表示的两个式子，最终可以得到

bORTB1(θ)=cλθ+c2−cb_{\mathrm{ORTB} 1}(\theta)=\sqrt{\frac{c}{\lambda} \theta+c^{2}}-c

即最优出价函数和θ\theta, λ\lambda, cc相关，λ\lambda的求解在后面会提到，固定λ\lambda，最优出价和θ\theta的关系如图Figure 2(b)所示。

Winning & Bidding Function 2

对于某些具有竞争性目标的广告系列，目标发布商/SSP设置了较高的底价，当出价价格约为0时，获胜的概率不会迅速增加；只有在买价大于某个非零值之后，获胜概率才开始急剧增加。这种情况通常发生在引人注目的广告位中。要获得此功能，对其稍加改动，并提出另一种获胜函数

w(b(θ))=b2(θ)c2+b2(θ)w(b(\theta))=\frac{b^{2}(\theta)}{c^{2}+b^{2}(\theta)}

其中c为常数，对于不同的c，获胜概率如Figure 3(a)所示。

可以推导得到最优出价函数为

bORTB2(θ)=b_{\mathrm{ORTB} 2}(\theta)= c⋅[(θ+c2λ2+θ2cλ)13−(cλθ+c2λ2+θ2)13]\quad c \cdot\left[\left(\frac{\theta+\sqrt{c^{2} \lambda^{2}+\theta^{2}}}{c \lambda}\right)^{\frac{1}{3}}-\left(\frac{c \lambda}{\theta+\sqrt{c^{2} \lambda^{2}+\theta^{2}}}\right)^{\frac{1}{3}}\right]

固定λ\lambda最优出价和θ\theta的关系如图Figure 3(b)所示。

关于最优出价函数的讨论

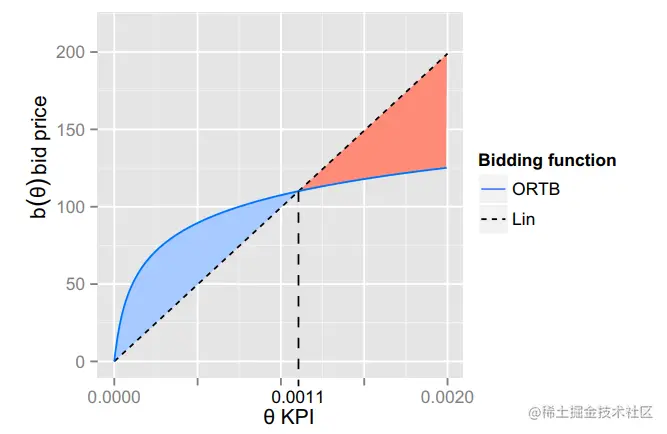
如下图所示，和线性的出价函数相比，在θ\theta小于0.0011时，文章中提出的最优出价函数给出了更高的出价；在θ\theta大于0.0011时，文章中提出的最优出价函数给出了更低的出价，主要特点有

  • 给更低价值的曝光给出更高的出价，获取更多的点击机会
  • 当获胜概率超过一定值时，提高出价并不会给获胜概率带来很大的提升，因此对于θ\theta高于一定值时，不给出过高的出价
  • 由于获胜相对于出价价格的凹凸性，ORTB策略（本文策略）将获得更大的获胜概率，而CPM只会增加一点点

λ\lambda求解

λ\lambda无法直接求得解析解，可以通过点击的日志数据求得数值解，有性质：当λ\lambda减少时，∫θb(θ)w(b(θ))pθ(θ)dθ\int_{\theta} b(\theta) w(b(\theta)) p_{\theta}(\theta) d \theta单调上升（解释看原文）。

具体求解方法在论文：Bid-aware Gradient Descent for Unbiased Learning with Censored Data in Display Advertising中有提到，可参考笔记：论文阅读 (010)。

3 实验准备

数据集介绍略，可以看原文。数据集中winning rate的展示如下，即随着出价价格提高，获胜概率提升；在出价过高时，获胜概率趋近于1，和文章提出的两种获胜函数在形式上一致。同时文章还讨论了特征和胜出价格的关系，结论就是胜出价格和特征无关，因此存在关系w(b(θ(x)),x)≡w(b(θ(x)))w(b(\theta(\boldsymbol{x})), \boldsymbol{x}) \equiv w(b(\theta(\boldsymbol{x})))，即胜出概率只和出价高低相关。

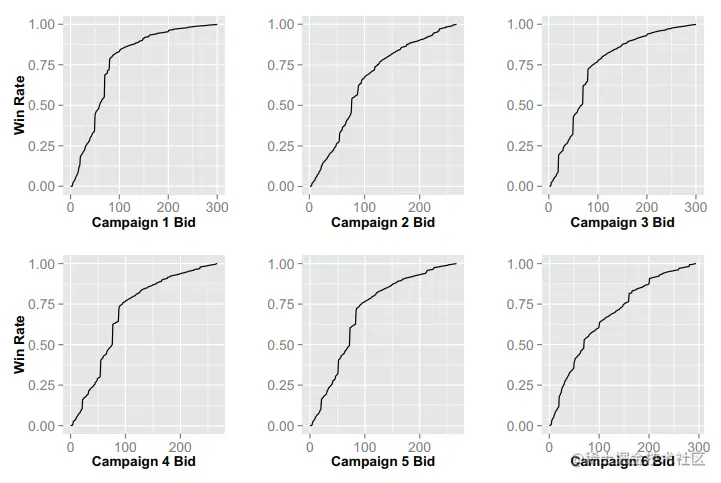
训练方法略，就是常规操作，此处记录测试的策略。评价流程如下图所示，只对竞价胜出的请求计算评价指标，但是无法获取竞价胜出后广告是否被点击和转化（这里文章用了别人的相关工作来解决，但是没有详细阐述）。为了测试不同预算约束下的性能，对于每个campaign，我们使用测试日志中原始总成本的1/64、1/32、1/16、1/8、1/4和1/2作为预算进行评价测试。

对比的方法有

  • Constant bidding (Const)：统一一个价格进行竞价，需要调节的是出价
  • Random bidding (Rand)：在一个范围内随意出价，需要调节的是价格范围的下界和上界
  • Bidding below max eCPC (Mcpc)：出价价格为max eCPC x pCTR。使用消耗费用/点击数目，计算每个campagin的max eCPC
  • Linear-form bidding of pCTR (Lin)：出价的方式为bLin⁡(θ)=b0θθ0b_{\operatorname{Lin}}(\theta)=b_{0} \frac{\theta}{\theta_{0}}，θ0\theta_{0}为目标条件下平均的CTR，b0b_{0}为基础的出价，需要调节b0b_{0}的值。
  • Optimal real-time bidding (ORTB1 and ORTB2)：本文提出的方法，c是通过拟合获胜概率得到，λ使用训练数据计算得到

以上方法的特点如下所示

4 线下实验

回答以下问题

  • 非线性竞价函数是否优于最先进的线性竞价函数，即ORTB1和ORTB2是否比Lin好
  • ORTB竞价的特点是什么？参数对ORTB效果有什么影响？预算情况对ORTB竞价有什么影响

出价策略对比

上述算法的对比效果如下图所示

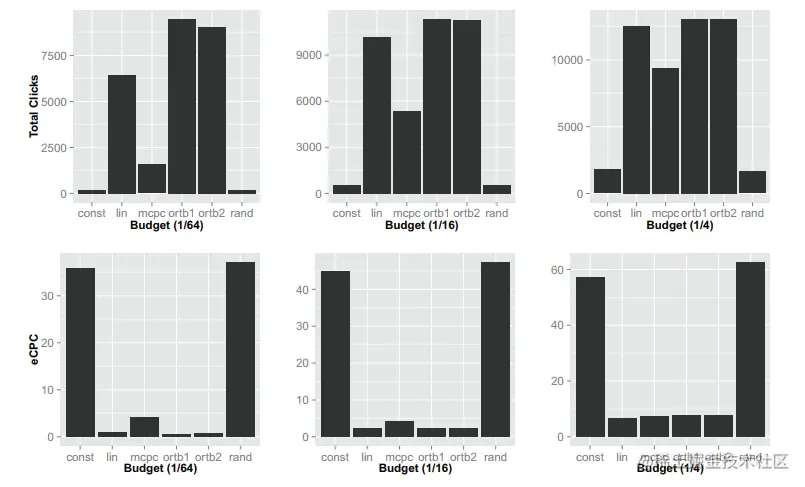
结论有

  • 在不同的预算下，ORTB1和ORTB2出价策略在点击数量上都有更好的效果，即说明非线性的竞价函数有效
  • 除了ORTB外，Lin效果最好，是目前在DSP被广泛使用的策略
  • Mcpc无法对不同的预算进行调节，当预算较低时，Mcpc的出价还是max eCPC x pCTR
  • Rand和Const的表现较差
  • 从eCPC看，Rand和Const会对于点击给出过高的出价

预算对出价策略影响

在不同的预算限制下，比较不同出价策略的效果，结果如Figure 10(a)所示

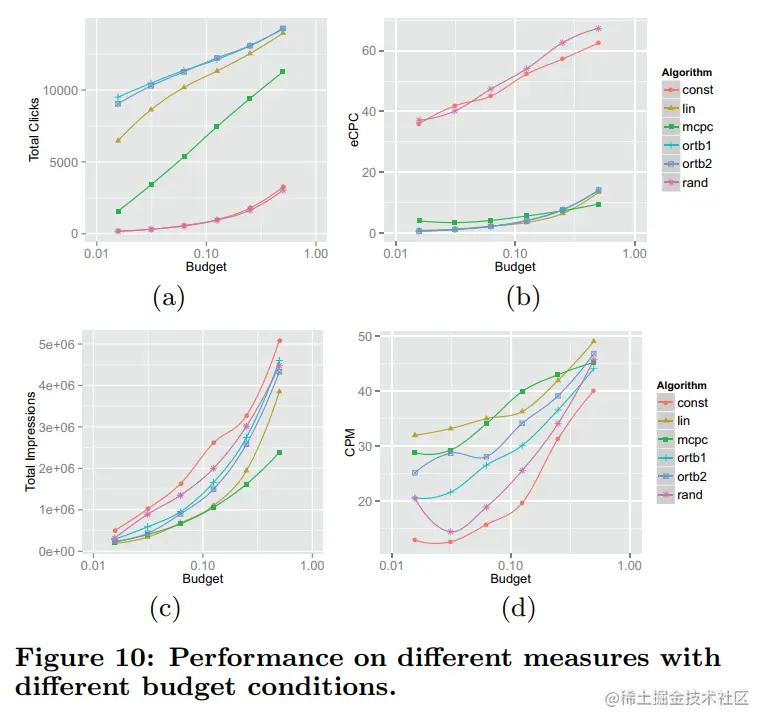
结论有

  • 当预算很低时（比如图中1/64），ORTB相对Lin在click上的提升很大（超过45%），这说明ORTB的出价策略在预算较低时表现很好，也验证了会给低价值的流量给出相对较高的出价
  • 当预算较大时，相对Lin的提升效果较小，即当预算充足的时候，会吧大部分预算从低价值流量移动到高价值的流量

点击和曝光对比

在图Figure 10(a)和Figure 10(b)中进行对比，有如下结论

  • 点击和eCPC都随着预算增加而增加，即当预算较低时，会在点价值的流量下进行出价，预算较高时，会在高价值的流量上出价
  • Mcpc对于出价不敏感，即eCPC相对来说变化很小
  • 当预算低时（小于等于1/16），ORTB和Lin的eCPC比Mcpc的eCPC小，预算高时（大于1/16），ORTB和Lin的eCPC比Mcpc的eCPC大

从Figure 10(c)和Figure 10(d)中可以看到，ORTB得到最高的点击的同时，也获得了相对较高的曝光，因为优化目标中同时优化的点击和曝光（即分别对应θ{\theta}和w(b(θ))w(b(\theta))）。

参数调整

对ORTB1和ORTB2，需要调整λ\lambda，在不同预算的情况下，λ\lambda和点击的关系如下图所示，在预算较低时，最优的λ\lambda较大，预算较高时，最优的λ\lambda较小，即预算较低时，出价会较低。

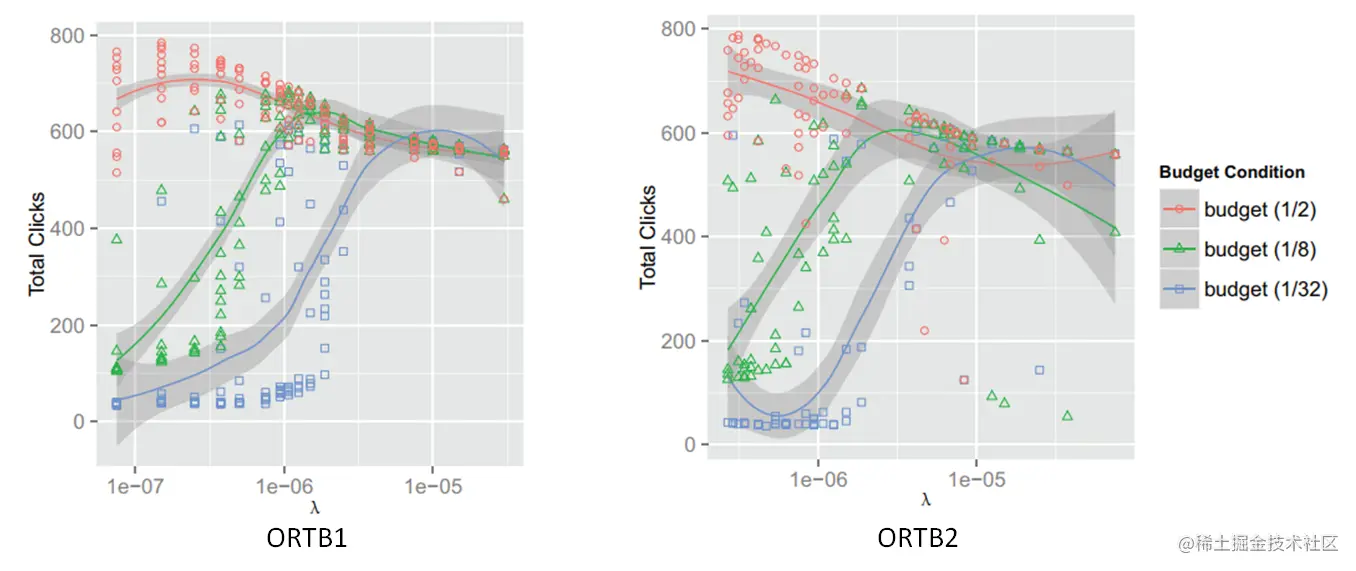
其他KPI指标

同时考虑点击和曝光，设置KPI如下

KPI=#\mathrm{KPI}=\# click +k⋅#+k \cdot \# conversion.

在文中实验时设置k=5k=5，优化时pKPI = pCTR + k.pCVR。实验结果如下图所示

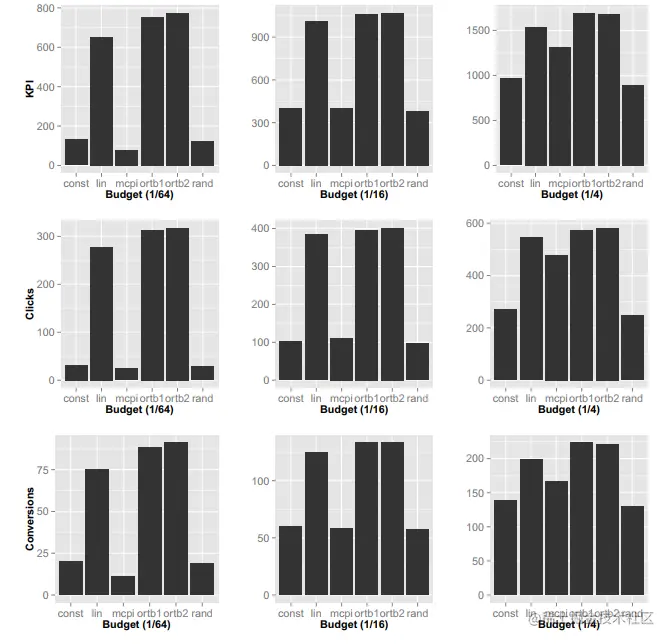
主要结论有

  • ORTB相对其他出价策略效果更好
  • 在预算限制为1/64的情况下，ORTB2比ORTB1效果更好，原因是winning function 2比winning function 1更适合上述的KPI优化目标

5 线上实验

线上实验时添加White策略（对符合特征和规则的广告出高价），实验结果如下图所示

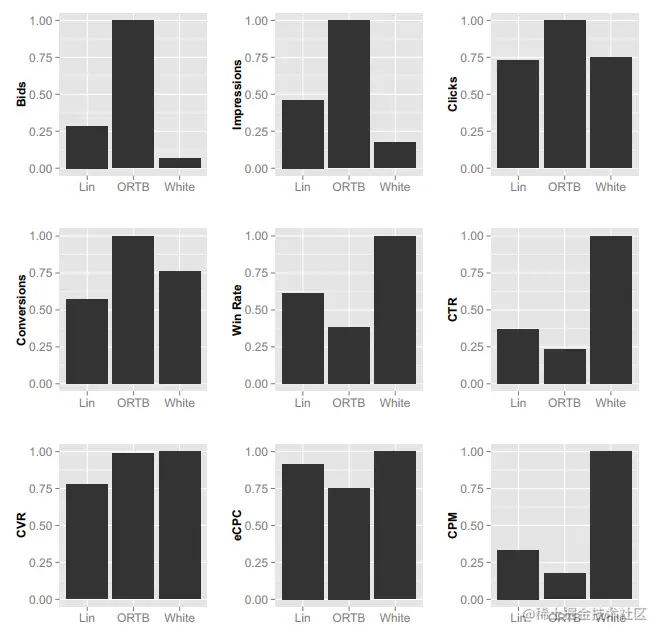
结论如下

  • ORTB比其他两种策略产生了更多的出价，得到了更多的曝光、点击、转化。同时ORTB取得了更低的eCPC，说明出价策略有效
  • ORTB获得了更低的CPM，原因时ORTB将较多的预算分配到低价值的流量
  • 由于低CPM和pCTR，ORTB拥有最低的拍卖中标率和点击率
  • White和ORTB出价策略相反，导致其中标数量低，CPM高

6 讨论

  1. 优化目标为：θw(b(θ))\theta w(b(\theta))，即考虑了胜出概率和点击率，那么如果胜出概率很高但是点击率低，是不是会导致最终转化数量低，这样的优化目标合理吗？

7 参考资料

  1. 【论文笔记】002 Optimal RealTime Bidding for Display Advertising

本文正在参与「掘金 2021 春招闯关活动」, 点击查看 活动详情

avatar
文章
阅读
粉丝