阅读论文：2011 Real-Time Bidding Algorithms for Performance-Based Display Ad Allocation

文章不是很好理解，因此笔记存在较多遗漏的地方。

背景

文章考虑了基于效果的展示广告分配问题。目标是将广告主（需求方）与广告展示次数（供应方）进行匹配，以使发布商角度（我理解是媒体）的总收入（也称为收益）最大化，同时满足主要由广告系列预算和供应清单带来的约束。主要贡献有以下几点

1. 提出了一种实时竞价算法，实现细粒度的曝光估值(如使用实时转换数据定位用户)，并根据实时约束快照(如预算消费水平)调整基于价值的竞价。
2. 在理论上证明了在线性规划(LP)原对偶公式下，简单实时竞价算法以对偶问题的最优解作为输入，确实是原对偶问题的在线求解方法。
3. 开发和验证两种实时出价调整方法，以适应市场的非平稳性质。

为什么要研究在线竞价，而不是离线的竞价，原因如下（以下为原文翻译，不知道理解的准不准确）

1. 离线全局优化只能在可观的曝光粒度级别上解决。例如，在当前针对一个大型展示广告网络的效果优化公式中，展示次数是在广告系列放置级别分配的，决策变量约为1M，约束条件约为0.5M。就估值而言，此粒度的每个节点内的展示均被视为同质的，因此无法利用更细粒度的展示数据。这些展示级别的机会中有一些是有区别的，例如用户的历史行为（只考虑广告位，没有实时考虑点击广告的用户）。
2. 即使某些限制是固有的，例如广告级别的预算限制和展示位置级别的流量，总之，随着广告主和发行商数量的增加，离线优化仍将变得很棘手。
3. 由于离线优化只能创建静态分配方案，因此缺乏一种自然的方式来适应市场动态。特别当从中得出中标的分布（出价情况）发生变化并且结果是竞选目标过高或过低时，离线算法就没有相应的调整机制。

文中几个相关概念

曝光价值

广告主（竞争者）在广告位上将广告曝光一次的价格，以CPC结算为：$eCPI = CTR \times CPC$，即点击率x点击价值。

点击率

即广告主投放的广告曝光时的点击率，计算方式为：$CTR = p(click|campaign, impression)$。

实时出价调整

根据当前竞争程度、约束满足情况对出价进行调整，调整方式为：$bid = eCPI - \alpha$。当bidding landscape变得竞争激烈时，调低$alpha$，甚至把$\alpha$调整为负数，以获取曝光机会。

问题建模

在线出价的目的是为了让总的收益最大，考虑约束有：

• 需求方面的约束(例如预算限制)，本文根据曝光传递目标(impression delivery goal)给出的
• 供给方约束，一次曝光只能分配给一个广告主

问题描述如下

• i表示n次曝光中的第i次，j表示m个广告主中的第j个
• $p_{ij}$表示第j个广告主获得第i次曝光时的CTR值，$q_j$表示第j个广告主的CPC出价，因此相应的eCPI表示为$v_{ij} = p_{ij}q_j$
• $g_j$是广告主j的impression delivery goal
• $x_{ij}$是决策变量，$x_{ij} = 1$表示将第i次曝光分配给广告主j，$x_{ij} = 0$表示不将第i次曝光分配给广告主j。

优化问题的原始表示如下，求解参数为$m\times n$个。

$\begin{array}{ll}\max _{x} & \sum_{i, j} v_{i j} x_{i j} \\ \text { s.t. } & \forall j, \sum_{i} x_{i j} \leq g_{j} \\ & \forall i, \sum_{j} x_{i j} \leq 1 \\ & x_{i j} \geq 0\end{array}$

对偶问题表示如下，求解参数为$m+n$个。

$\min _{\alpha, \beta} \sum_{j} g_{j} \alpha_{j}+\sum_{i} \beta_{i}$

s.t. $\forall i, j, \alpha_{j}+\beta_{i} \geq v_{i j}$

$\alpha_{j}, \beta_{i} \geq 0$

对偶问题中变量的直观解释

• $\alpha_j$为广告主j获得额外目标曝光的经济价值（例如，通过增加预算，文中也理解为最小利润）
• $\beta_i$为媒体获得额外曝光i的经济价值（例如，吸引更多访问者）

从上面建模后，问题有

1. 如何以在线方式从对偶的最优解中得出对原始问题的最优解
2. 如何解释曝光数到达分布的非平稳性质（没理解这是什么问题）

实时出价算法

在线出价算法如下，考虑每次曝光i到达时，需要进行实时的出价，即求解$x_{ij},\forall j$。在原问题中，需要求解m个变量$x_{ij},\forall j$，变量满足一个约束$\sum_j x_{ij} \leq 1$，在对偶问题中，需要求解一个变量$\beta_i$，变量满足m个约束条件$\alpha_j + \beta_i \geq v_{ij} \forall j$。

在线算法使用互补松弛度定理来分配变量，从而保持离线最优状态。

• 对于曝光i和广告主j的价值为$v_{ij}$，从而出价为$v_{ij} - \alpha_j$，最大出价的广告主获得曝光的机会，goal-achieved campaigns的广告主退出出价
• $\beta_i$是用来记录曝光i的经济价值的，对拍卖并不重要
• $\alpha_j = UpdateAlpha(\alpha_j)$表示根据目标完成的程度和出价环境对$\alpha_j$进行调整。在平稳印象到达假设下，它简化为一个恒等函数(Under a stationary impression arrival assumption, it reduces to an identity function)
• 从竞价的角度来看，$\alpha_j$表示广告主需要最小的利润，因此可以理解为可以最多可以出价为$v_{ij} - \alpha_j$；$\beta_i$应与售卖曝光i的媒体要求的底价成正比

上述算法在平稳α假设下，建立了该基本在线竞价算法的离线最优性

文中定理2

通过上述算法，给定最佳出价调整$\alpha_j, \forall j$，采用以下设计的首次拍卖(first-price auction)，可确保离线优化。

1. 对于每次曝光i，广告主j出价为$v_{ij} - \alpha_j$
2. 只有活跃的广告主可以参与竞价，即满足条件：$\sum_{i^{'}j}x_{i^{'}j} < g_j$
3. 曝光分配只分配给最高的出价并且最高出价为正数，即$v_{ij} - a_j > 0$

分别对上述进行证明（此处参考了参考资料1）

1. 如果最高出价$v_{ij^{*}} - \alpha_{j^{*}}>0$，则曝光i一定会分配。假如不进行分配，则原问题中$\sum_j x_{ij} < 1$，根据线性松弛定理，可得$\beta_i = 0$，由对偶约束中$\alpha_{j^{*}} + \beta_i \geq v_{ij^{*}}$可知，$\alpha_{j^{*}} \geq v_{ij^{*}}$即$\alpha_{j^{*}} - v_{ij^{*}} \geq 0$，与$v_{ij^{*}} - \alpha_{j^{*}}>0$矛盾
2. 曝光i一定会分配给广告主$j^{*}$，假如分配给广告主$j^{'}$，则$x_{ij^{'}}=1$。根据互补松弛定理，得到$\alpha_{j^{'}} + \beta_i = v_{ij^{'}}$。如果$j^{*}\neq j^{'}$，则存在$v_{ij^{*}} - \alpha_{j^{*}} > v_{ij^{'}} - \alpha_{j^{'}} = \beta_i$，$v_{ij^{*}} > \alpha_{j^{*}} + \beta_i$，与约束$\alpha_{j^{*}} + \beta_i \geq v_{ij^{*}}$矛盾
3. 如果最高出价$v_{ij^{*}} - \alpha_{j^{*}} < 0$，则曝光i不进行分配。如果将i分配给j，则$x_{ij} = 1$，根据互补松弛定理$\alpha_{j^{*}} + \beta_i = v_{ij^{*}}$，其中$\beta_i \geq 0$，所有$a_{ij} \leq v{ij}$，与$v_{ij^{*}} - \alpha_{j^{*}} < 0$矛盾
4. $v_{ij^{*}} - \alpha_{j^{*}} = 0$，则存在多个最优解

出价调整

上述算法假设曝光的分布是固定的，即有足够的数据情况下可以学习最优的出价调整$\alpha_j$。然而市场是动态的，因此曝光是不稳定的，$\alpha_j$是一个时变的值，非平稳条件违反互补松弛条件，需要对$\alpha_j$进行调整。文章先用历史数据导出的对偶的离线最优解初始化$\alpha_j$，然后通过控制理论或统计方法在线更新$\alpha_j$以适应供给侧动态和需求侧约束满足水平。

控制理论出价调整

使用PI控制器进行调整，记t时刻期望和观测的出价获胜概率分别为$r_j(t)$，$r^{'}_j(t)$，误差为$e_j(t) = r_j(t) - r^{'}_j(t)$，调整方式为：$\alpha_{j}(t+1) \leftarrow \alpha_{j}(t)-k_{1} e_{j}(t)-k_{2} \int_{0}^{t} e_{j}(\tau) d \tau$。其中$k_1$为比例增益，$k_2$为积分增益，$t\in[1, 2, ..., T]$，其中t为极小的时间间隔数目，T为时间间隔个数。

另外一种为waterlevel-based更新，调整方式为：$\alpha_{j}(t+1) \leftarrow \alpha_{j}(t) \exp \left(\gamma\left(x_{j}(t) / g_{j}-1 / T\right)\right), \forall j$。其中$x_{j}(t)$表示在第t个时间间隔中，用户$j$获得曝光的次数，$\gamma$用于调节对于误差响应的速度，误差为$x_{j}(t) / g_{j}-1 / T$。

waterlevel-based更新有较好的链式性质，可以写作

$\alpha_{j}(t+1)=\alpha_{j}(t) \exp \left(\gamma\left(x_{j}(t) / g_{j}-1 / T\right)\right)$

$\quad=\alpha_{j}(t-1) \exp \left(\gamma\left(\sum_{\tau=t-1}^{t} x_{j}(\tau) / g_{j}-2 / T\right)\right)$

$\quad=\ldots$

$\quad=\alpha_{j}(1) \exp \left(\gamma\left(\sum_{\tau=1}^{t} x_{j}(\tau) / g_{j}-t / T\right)\right)$

统计方法出价调整

此处方法没看懂，仅作记录

当出价为$b_{ij} = v_{ij} - \alpha_j$时，胜出概率为：$p\left(w \leq b_{i j}\right)=\int_{-\infty}^{b_{i j}} f(w ; \theta) d w=F\left(b_{i j} ; \theta\right)$。其中$w \sim \mathcal{P}(\theta)$，$\theta$为模型参数

出价调整方式为：$\alpha_{j}(t+1) \leftarrow \alpha_{j}(t)-\gamma\left(F^{-1}\left(r_{j}(t)\right)-F^{-1}\left(r_{j}^{\prime}(t)\right)\right), \forall j$。其中$r_j(t)$，$r^{'}_j(t)$分别为期望和观测的出价获胜概率，$\gamma$用于调节对于误差响应的速度。

更实际的出价方式

上述出价算法为最基本算法形式，建立了在平稳曝光到达假设下的最优性。在LP的基本公式中，约束被编码为曝光传递目标(impression delivery goal)，曝光被单独评估和分配。这部分建立了更为一般的优化目标和约束形式，如下所示

1. i表示n次曝光组中的第i次，曝光组被认为无法区分，即CTR一致，例如同一个展示位置
2. $g_j$表示广告主j的预算
3. $h_i$表示媒体组i可以被展示的次数
4. $x_{ij}$表示将媒体组i分配给广告主j
5. $w_i$表示第i组的每次展示（流量获得）成本，例如，维克雷拍卖(Vickrey auction)中的第二个价格

原始线性规划问题表示如下

$\begin{array}{ll}\max _{x} & \sum_{i, j}\left(v_{i j}-w_{i}\right) x_{i j} \\ \text { s.t. } & \forall j, \sum_{i} v_{i j} x_{i j} \leq g_{j} \\ & \forall i, \sum_{j} x_{i j} \leq h_{i} \\ & x_{i j} \geq 0\end{array}$

对偶问题表示如下

$\min _{\alpha, \beta} \sum_{j} g_{j} \alpha_{j}+\sum_{i} h_{i} \beta_{i}$

s.t. $\forall i, j, \quad v_{i j} \alpha_{j}+\beta_{i} \geq v_{i j}-w_{i}$

$\quad \alpha_{j}, \beta_{i} \geq 0$

和基本的形式一致，解法如下

1. 每个广告主j根据来自第i组的曝光进行竞价，金额为$v_{ij}(1-\alpha_j)$，出价调整项$\alpha_j$为广告活动所需的最低利润率（利润除以收入）
2. 只有活跃的广告主可以参与竞价，满足条件$\sum_{i}v_{ij}x_{ij} < g_j$
3. 仅当最高出价大于费用$w_i$时才分配展示，成本项wi是恒定的

实验

回答了3个问题

1. 在给定最优竞价调整$\alpha_j$的情况下，在线竞价算法是否可以获得线下收益最优?
2. 不同出价调整方法的效果如何？是否可以逼近最优值？控制性质怎么样？
3. $\alpha_j$的初始值选取方式有多大意义?

实验中方法具体实现建议读原文，细节有点多，此处不做记录

评价指标有

Revenue lift $=\frac{y^{\prime}}{y}=\frac{\sum_{t, i, j} x_{i j}^{\prime}(t) p_{i j} q_{j}}{\sum_{t, i, j} c_{i j}(t) q_{j}}$

$\mathrm{CTR} \operatorname{lift}=\frac{\mathrm{CTR}^{\prime}}{\mathrm{CTR}}=\frac{\sum_{t, i, j} x_{i j}^{\prime}(t) p_{i j} / \sum_{t, i, j} x_{i j}^{\prime}(t)}{\sum_{t, i, j} c_{i j}(t) / \sum_{t, i, j} x_{i j}(t)}$

其中$p_{ij}$为empirical CTR，$q_j$为出价，因此Revenue lift表示为收益相对实际的提升，CTR lift表示为点击率相对实际数据提升。

在线和离线对比

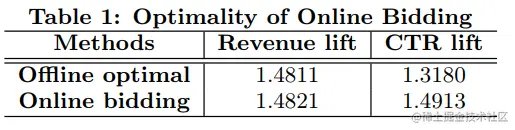
离线比在线结果还好，理由如下

1. 批处理曝光中分配了共享相同的复合键（t; i; j）来节省计算量，这可能违反库存约束
2. 在线算法只会为曝光分配正的中标出价，而可能会忽略不可获利的曝光，离线算法没有考虑此约束调整，因此存在负的出价

控制出价策略对比

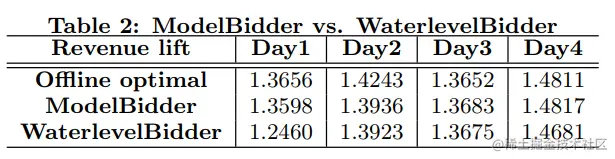
结论有

1. 所有的出价调整策略都较好地逼近了离线最优，在离线效果的90%以上
2. model-based的调整比waterlevel-based效果好

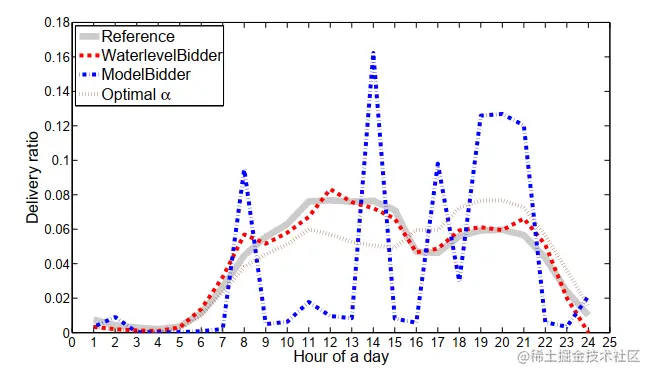
定义以下指标

• 每小时投放比例(hourly delivery ratio)：每小时获胜曝光占日投放目标的百分比
• 每小时参考比例(hourly reference ratio)：每小时曝光到达量占每日总曝光数的百分比

稳定的控制策略应该使得投放比例接近参考比例，实验结果如图所示。waterlevel-based具有出色的稳定性，因为它可以直接针对参考值测量误差，而model-based则表现出更大的振荡。另一方面，使用静态最优$\alpha_j$对参考没有反应。

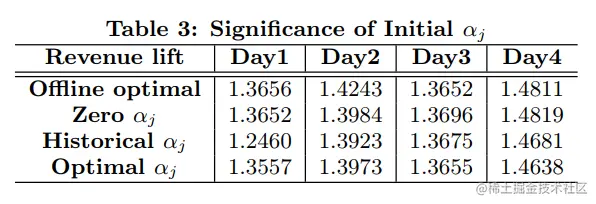
初始$\alpha_j$选取

比较三种选取策略

1. 初始$\alpha_j$为0
2. 初始$\alpha_j$为历史最优$\alpha_j$
3. 初始$\alpha_j$为离线最优$\alpha_j$

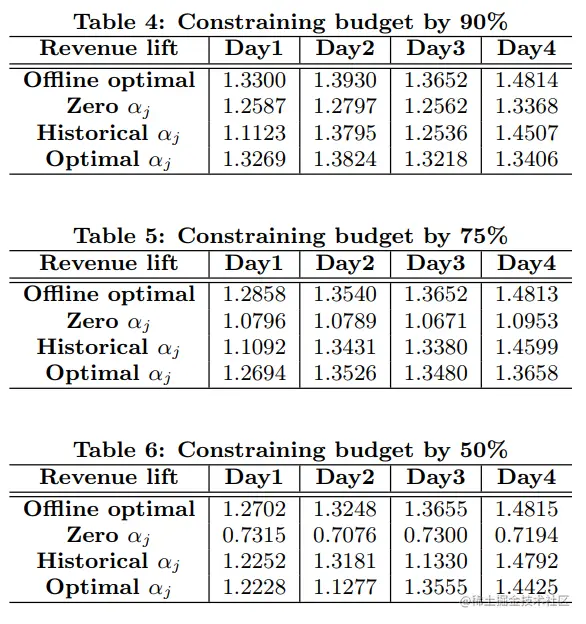
实验结果如下，初始$\alpha_j$采样不同策略时，效果相近，作者给出的解释是：

We argue that this may be an artifact of offline simulation, where only offline data pre-filtered by the current production system could be obtained.The actual impression allocation in the data has already gone through constraint enforcement by the current delivery system that produces the data; and as a consequence, the delivery goal for the online bidding simulation will not be constraining enough to make αj

使用不同的预算约束，实验结果如下，随着预算减少，使用0初始化$\alpha_j$的效果变差，通过历史或离线初始化$\alpha_j$则保持了较好的效果。

讨论

目前读的最难受的论文ORZ，全文读下来有较多的疑问，此处做记录

1. 统计方法出价调整具体怎么实现？

2. 在更时的出价形式中，曝光粒度变为了媒体组，这么做的意义是什么？

看似回答是

As one wishes to valuate impressions at a very fine-grained level, the primal will soon become intractable (recall the cream-skimming problem). We propose a dual-based approach as follows.

3. 在线出价不是最优解，但是比离线效果更好，是不是可以通过添加约束条件获得更好的离线效果

参考资料

1. [广告-机制策略-流量分配]收入最大化的流量分配策略