分治

• 找到重复性 大问题细分成子问题
• 子问题的结果进行合并

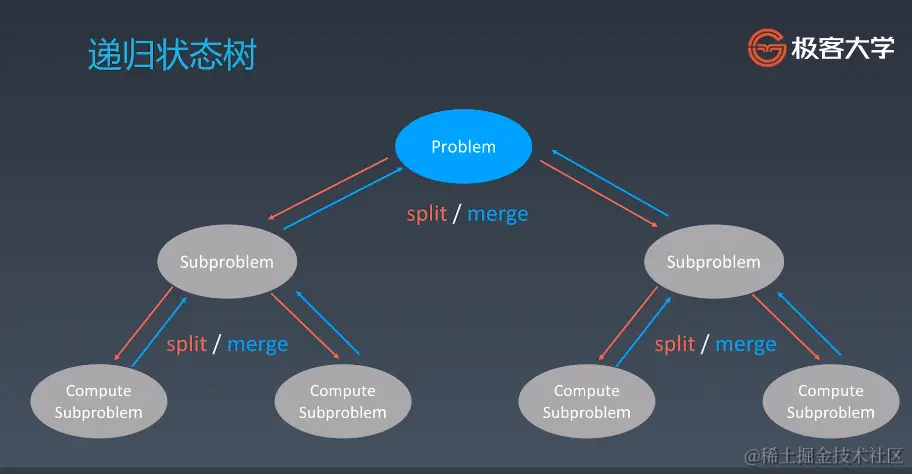
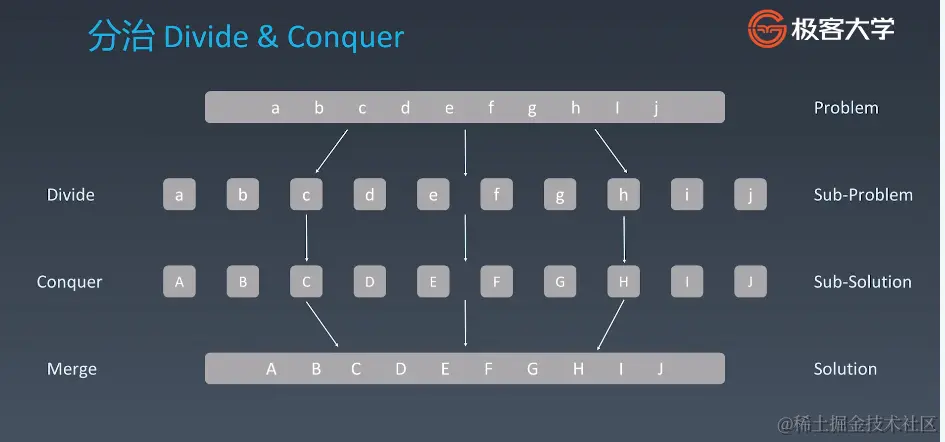
示例

代码模板

• 问题解决 终止条件
• 处理当前逻辑 如何分成子问题(比较重要)
• 下探到下一层 解决细分的子问题、合并子问题的结果 组装到一起
• 清除当前层的变量 将不是本地局部的变量恢复原样

# Python
def divide_conquer(problem, param1, param2, ...): 

  # recursion terminator 
  # 问题解决 终止条件
  if problem is None: 
	print_result 
	return 

  # prepare data 
  # 处理当前逻辑 如何分成子问题
  data = prepare_data(problem) 
  subproblems = split_problem(problem, data) 

  # 下探到下一层 解决细分的子问题
  # conquer subproblems 
  subresult1 = self.divide_conquer(subproblems[0], p1, ...) 
  subresult2 = self.divide_conquer(subproblems[1], p1, ...) 
  subresult3 = self.divide_conquer(subproblems[2], p1, ...) 
  …

  # process and generate the final result 
  result = process_result(subresult1, subresult2, subresult3, …)
	
  # revert the current level states

50. Pow(x, n)

class Solution:
    """
    思路:
        1. 暴力破解 循环N次 数字*N次 进行累乘

        2. 分治 log(N)
            - 转换成子问题
                - terminator
                - process(split problem )
                - dril down(sub problem)、 merge(sub result)
                - reverse states

            一分为二
                subproblem: subresult = pow(x, n/2)

                merge:
                 奇数 if n % 2 == 1 : subresult * subresult * x
                 偶数 else  subresult * subresult


    """

    def myPow(self, x, n):
        """

        :param x:
        :param n:
        :return:
        """

        def quick_pow(N):

            # 终止条件
            if N == 0:
                return 1.0

            # 细分成子任务
            half = quick_pow(N // 2)

            # 合并结果

            if N % 2 == 1:
                # 奇数次幂
                return half * half * x
            else:
                # 偶数次幂
                return half * half

        if n < 0:
            return 1/quick_pow(-n)
        else:
            return quick_pow(n)

回溯

• 采用试错的思想 尝试分步去解决问题
  • 在分步的过程中 如果得不到答案 将取消前面的计算
  • 再通过其他的可能分步解答 尝试寻找答案
• 使用递归方法
• 八皇后 数独问题