写在前面：在UPM领域中，该篇2018年的算法算是比较新的，相比于之前的 KHMC 和 TKO 两篇算法，该算法能够在早期运算过程中快速提高阈值，这在密集型数据集中的表现是十分有利。

THUI算法

样例

• 各项的TWU：

  

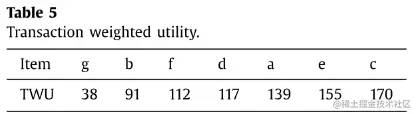
• 数据集：

  

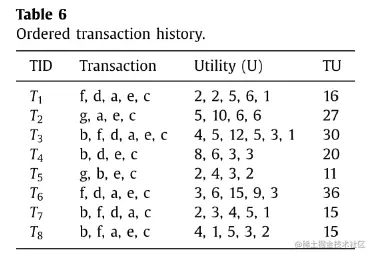
• 各项排序：

  $$c \succ e \succ a \succ d \succ f \succ b \succ g$$

定义

该章节和之前的 top-$k$ 算法没有区别，具体可以参考EHIN, EFIM等几篇算法的描述

Leaf itemset utility (LIU) data structure

LIU 是一个三角矩阵，由多组连续的项组成，$(x_{\rm i} \dots x_{\rm j})$ 意味着一组项从 $x_{\rm i}, x_{\rm i+1}, x_{\rm i+2} \dots$ 直到 $x_{\rm j}$，而且这些项都是有序排列的。每一列表示以当前元素作为当前序列中的最后一个元素（即 $x_{\rm j}$），每一行的元素作为当前序列中的第一个元素（即 $x_{\rm i}$），可以对照参考下图示例（计算 $T_1$ 后的 LIU）：

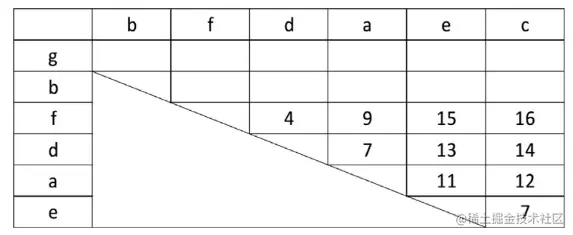
策略

LIU strategy

在实际代码中，采用的是HashMap来实现该结构，因为该矩阵只是存储一串连续序列的效用值信息，所以真正需要的内存并不大。（是不是和KHMC算法的EUCS很相似？？？）

Threshold raising strategies

• RIU

  老方法了，利用一元项集进行阈值提升

• RUC

  RIU 的plus版，利用多元项集进行阈值提升，在FHM算法中有详细介绍

• LIU-E

  在生成_LIU_矩阵之后，利用优先队列（PQ_LIU）存储那些不低于初试阈值的项的效用值，有如下公式： $PQ\_LIU = \{LIU(x, y)|LIU(x, y) \ge \delta \}$。当队列中存储到k个元素时，把第k个元素的效用值作为新的阈值【因为优先队列内置排序功能，而且选择第k个意味着前面的k-1个元素的效用值都大于现在选择的阈值】

• LIU-LB

  该方法利用LIU矩阵的连续项集信息，来估计其它相关项集的下边界值，有以下性质：

  1. 累积效用属性（Cumulative utility property）对任意 $X,Y$ 是不相交的项集，有 $U(X) + U(Y) \ge U(X \cup Y)$ 证明如下：

     $$U(X) + U(Y) = \sum_{(X \cup Y) \subseteq T_{\rm j}}U(X, T_{\rm j}) + \sum_{(X \cup Y) \not \subseteq T_{\rm j} \cap X \subseteq T_{\rm j}}U(X, T_{\rm j}) \\ + \sum_{(X \cup Y) \subseteq T_{\rm j}}U(Y, T_{\rm j}) + \sum_{(X \cup Y) \not \subseteq T_{\rm j} \cap Y \subseteq T_{\rm j}}U(Y, T_{\rm j}) \\ U(X \cup Y) = \sum_{(X \cup Y) \subseteq T_{\rm j}}U(X) + \sum_{(X \cup Y) \subseteq T_{\rm j}}U(Y)$$

  2. 低效用边界属性（Utility lower bound property）存在低效用边界项集 $Y$，对任意项集 $X$ 有如下公式

     $$ULB(Y) = U(X \cup Y) - U(X) = U(X \cup Y) - \sum_{x_{\rm i} \in X}U(x_{\rm i})$$

  3. LIU-Lower Bound（LIU-LB）设 $PQ\_ALL = \{PQ\_LIU \cup PQ\_LB\_LIU \}$，当 $PQ\_ALL$ 的长度超过 $k$ 时，阈值提升为该列表中第 $k$ 个元素的效用值

  伪代码如下：

  

算法

THUI Algorithm

该算法在对检索空间剪枝上，采用了 TWU-prune, U-prune, LA-prune 等三种策略，这些策略都是使用现成的算法，只是工作的环节不同，在文中均有指出

Explore Search Tree

该函数和HUI-Miner的检索算法一致，同样还采用了FHM算法中的RUC策略来提升阈值

总结

该算法提出了一种新的数据结构—— Leaf Itemset Utility (LIU)，该数据结构优势在于只需要很小一部分内存就可以存储。其次，该算法还设计了一种新的效用下限估计方法—— lower bound estimation method(LIU-LB) 这是一个比较偏的角度（因为这样考虑意义不大），之前我们大多考虑的是上边界。本质上该算法是基于 utility-list 结构设计的 one-phase 算法，在性能上要好过 TKO 和 KHMC。