概述
分类->虚拟变量->逻辑回归

逻辑回归得出的表示的是苹果的的概率,
则是苹果,
则是橙子
逻辑回归:线性概率模型(Linear Probability Model,简记LPM)

- 内生性问题:扰动项μ和自变量有关系=协方差不为0,会导致回归效果差
有可能出现负数==负概率或者>1两种无意义的情况
通过连接函数F将上述式子进行改进,解决负概率和>1的问题

现在要选择一个合适的F连接函数:标准正态分布的累计密度函数or sigmoid函数

☆意义: 回归式子变为F(y)=F(x,β),F(y)的结果是一个[0,1]的数,F是sigmoid函数,现在要做的就是通过这个式子去估计参数β的值==>非线性模型使用极大似然估计方法(MLE) 对参数β进行估计(注:线性模型就可以用最小二乘法来估计参数(见前面的多元线性回归))
y=f(x,β)--->F(y)=F(x,β)--->极大似然估计--->梯度下降求解非线性最大化问题
求出β参数后,就得到了模型,现在给定自变量x,扔进去得到的就是概率


线性概率模型spss实操
为什么用spss:
- 因为不仅可以求解逻辑回归,也可以求fisher回归
- stata保存变量比较麻烦
假如自变量有定性变量:

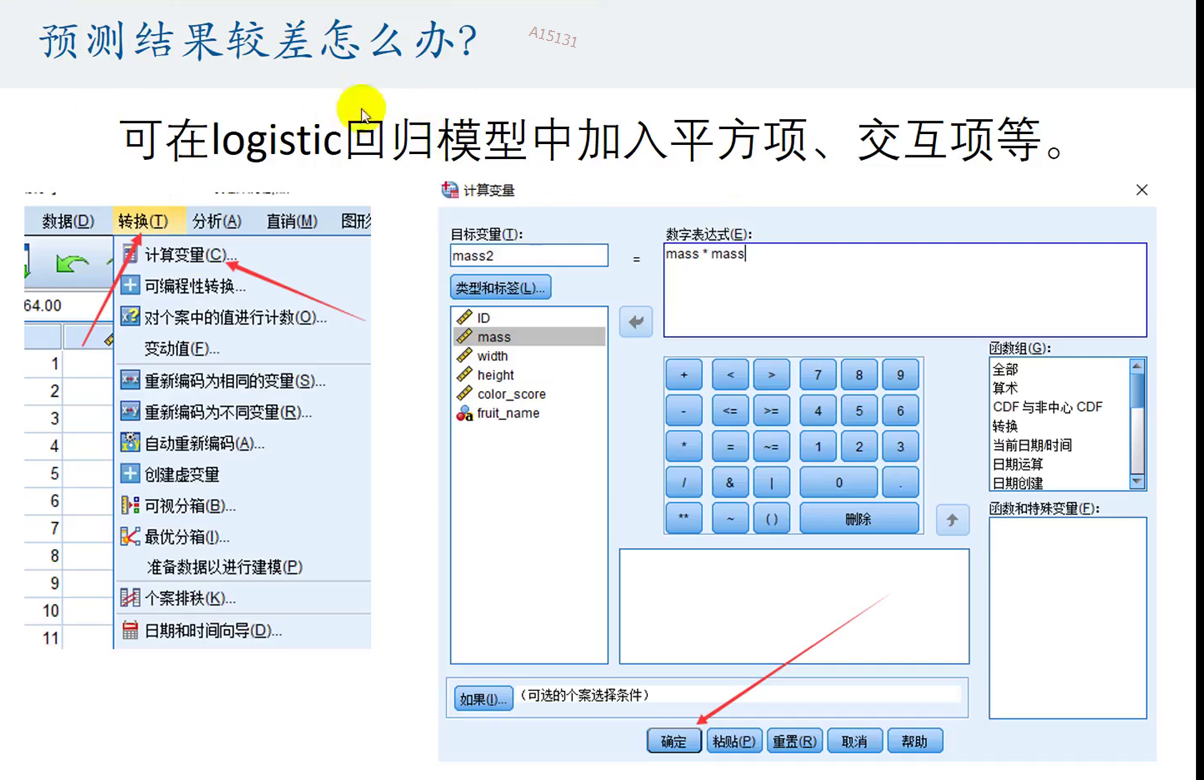
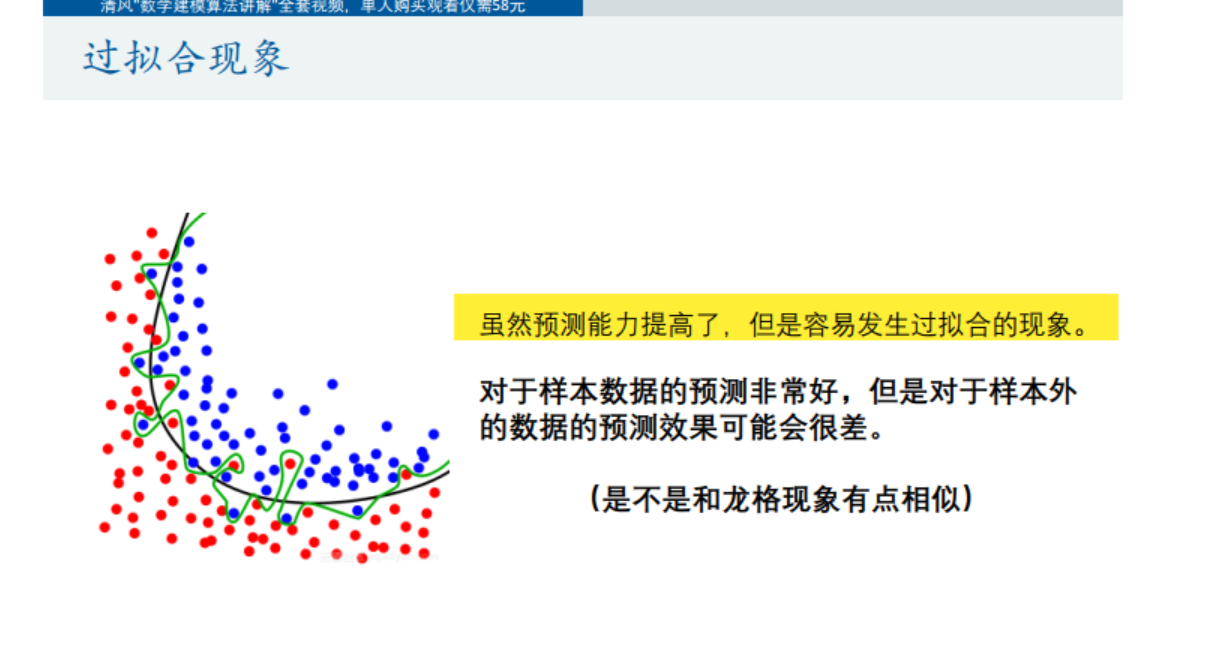
预测效果不好怎么办:加入平方项变量,交互项---->但会产生过拟合现象

Fisher线性判别分析
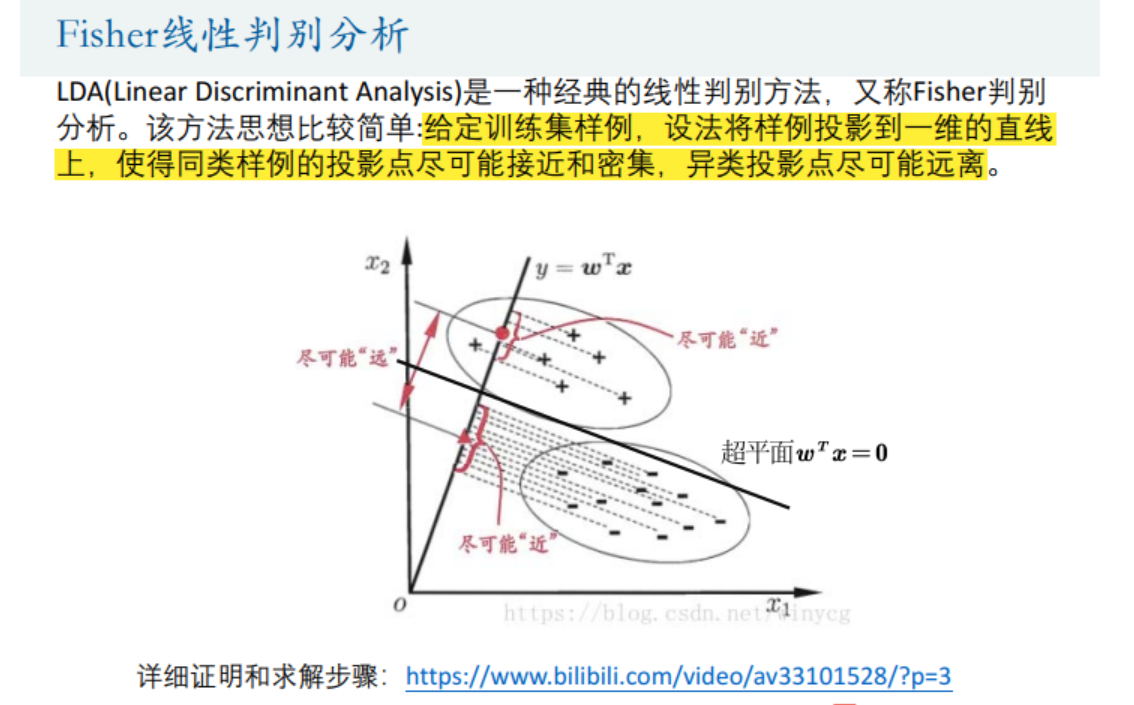
思想: 将所有的点用一个超平面分隔开<=>将每个点投影到ω这个法向量上,保证:类内小,类间大,实现了p维数据降为1维。
做法: 定义类间距离,类内距离,定义目标函数,求出目标函数的最大值对应的ω,现在给一个新的数据,只要计算
就可以判断是在超平面的哪一侧,即分类成功。
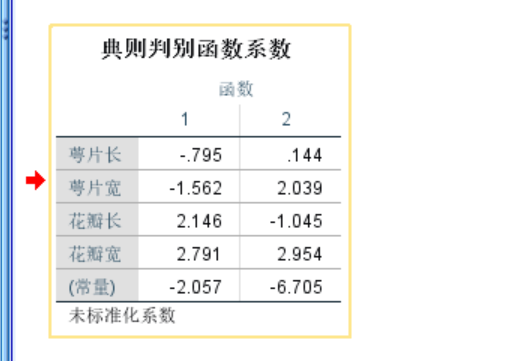
核心问题: 找到线性系数向量ω
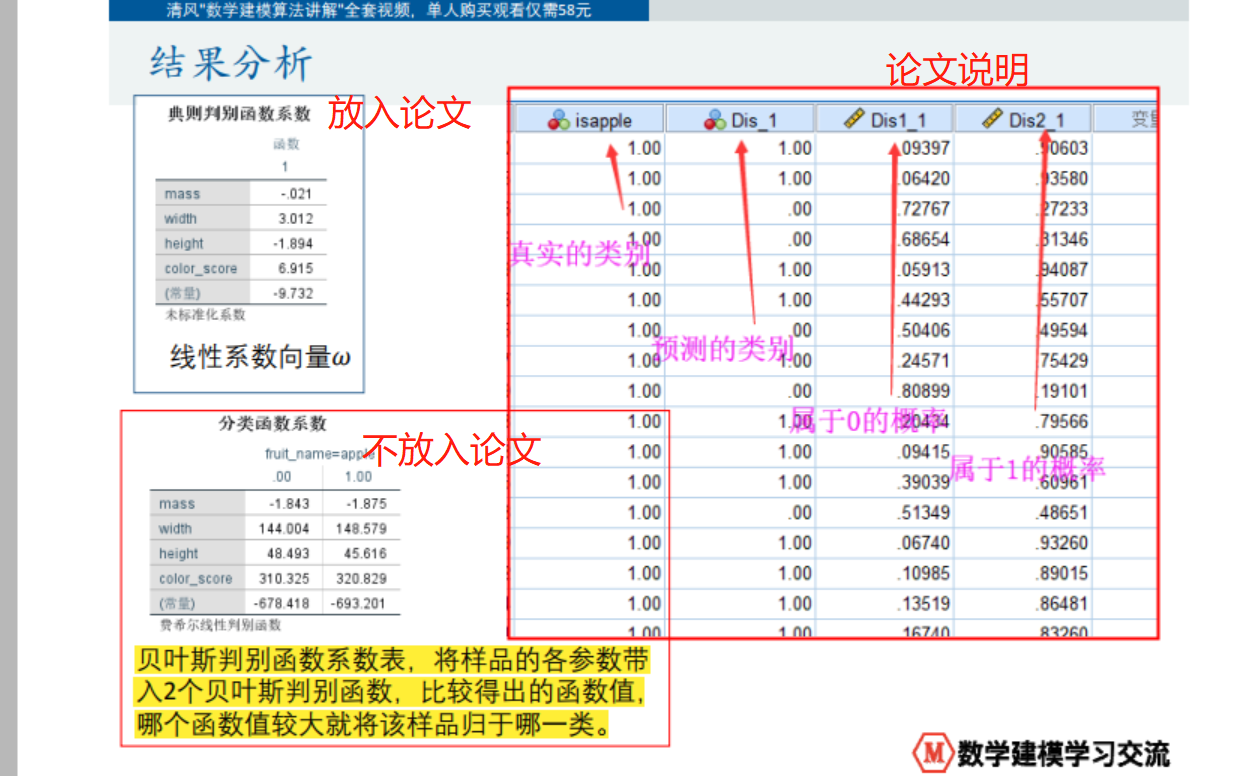
Fisher线性判别分析SPSS实操
多分类问题
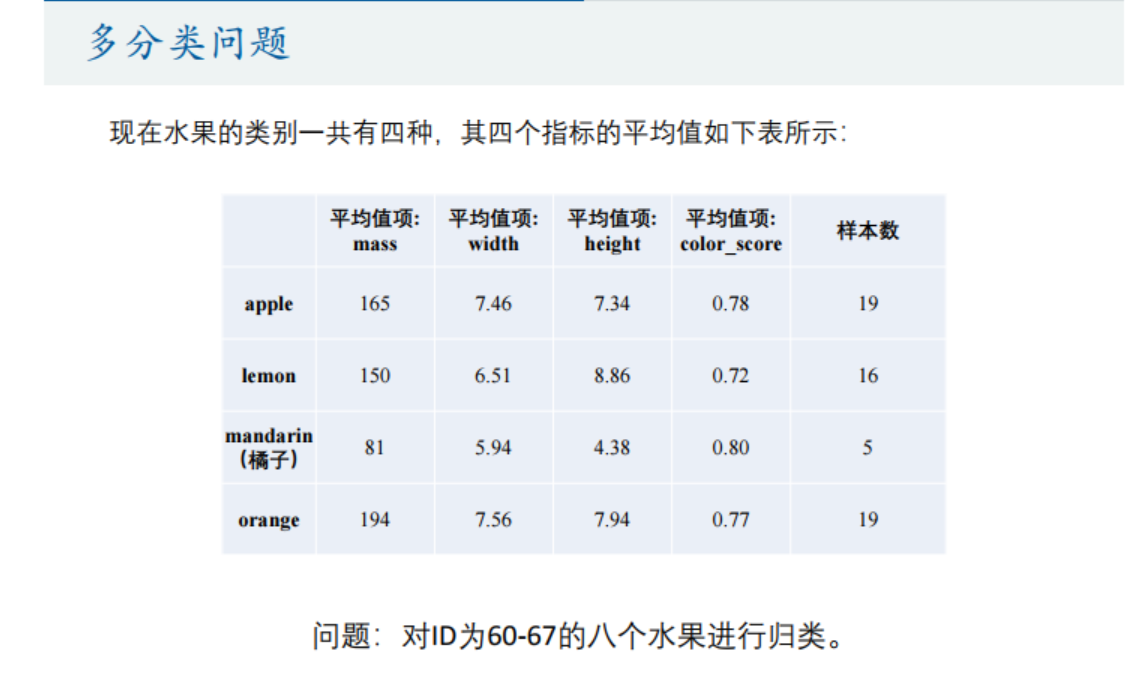
Fisher判别分析可用于多分类 :blog.csdn.net/z962013489/…
Logistic回归也可用于多分类 :将连接函数:Sigmoid函数 推广为 Softmax函数;使用多元逻辑回归,可能会存在过拟合问题->采用训练组测试组的交叉验证模型
实操过程
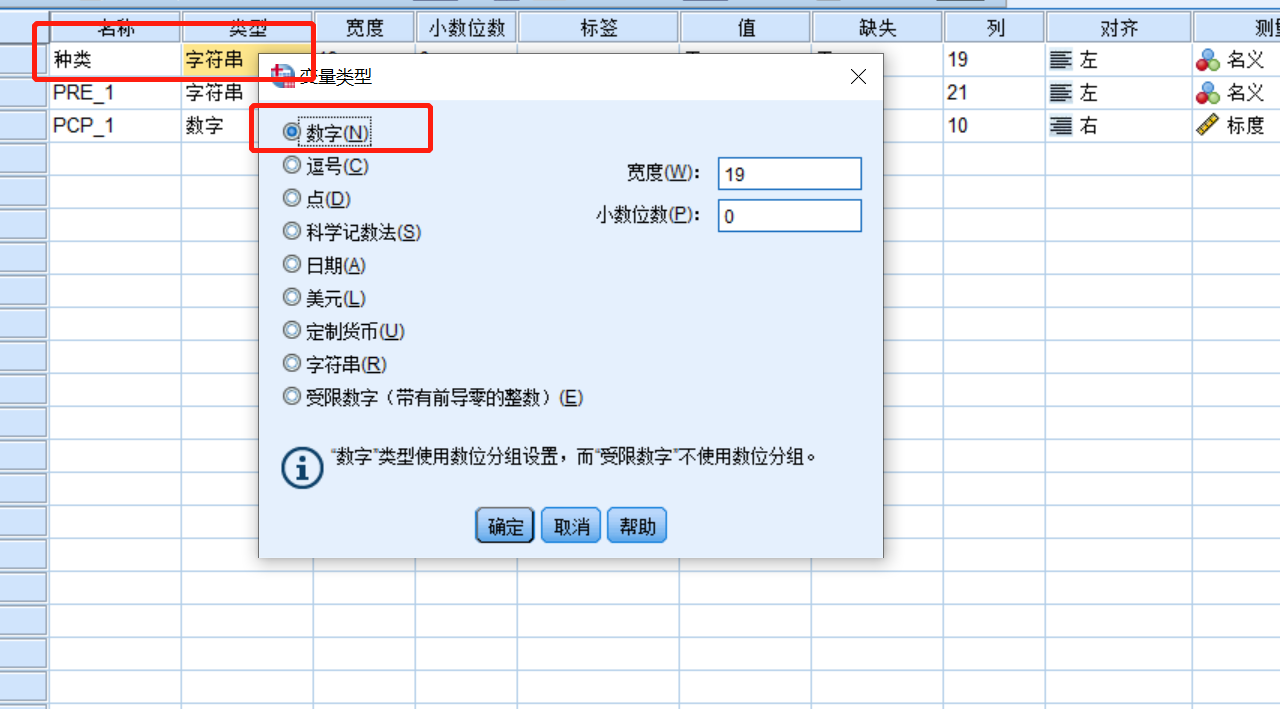
生成虚拟变量,和多元回归用行向量不同(其实多元回归用123表示会不会更方便?),这里用excel替换功能换成1,2,3就行了
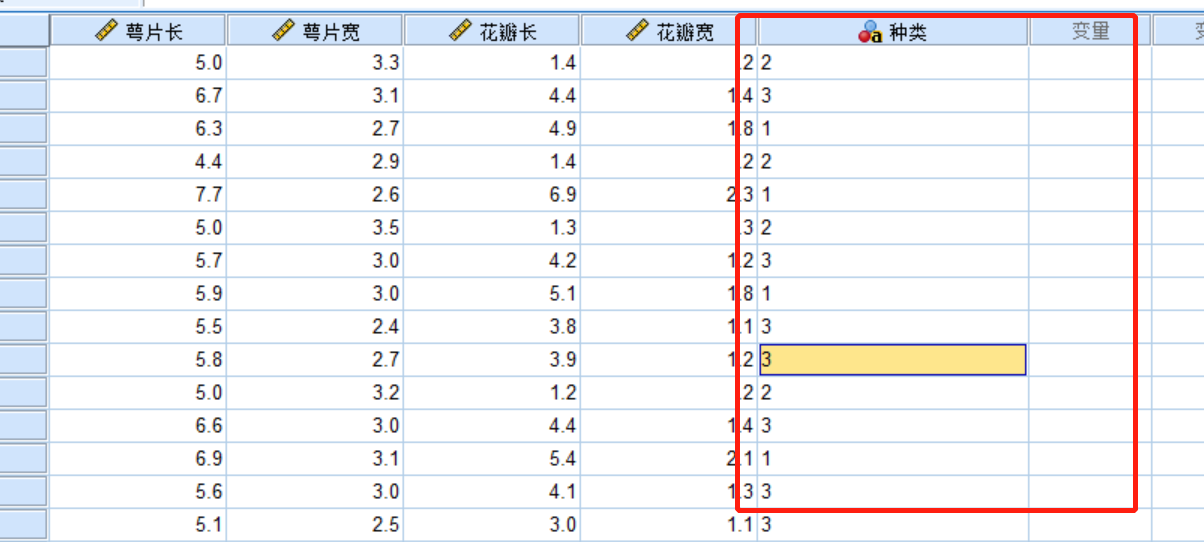
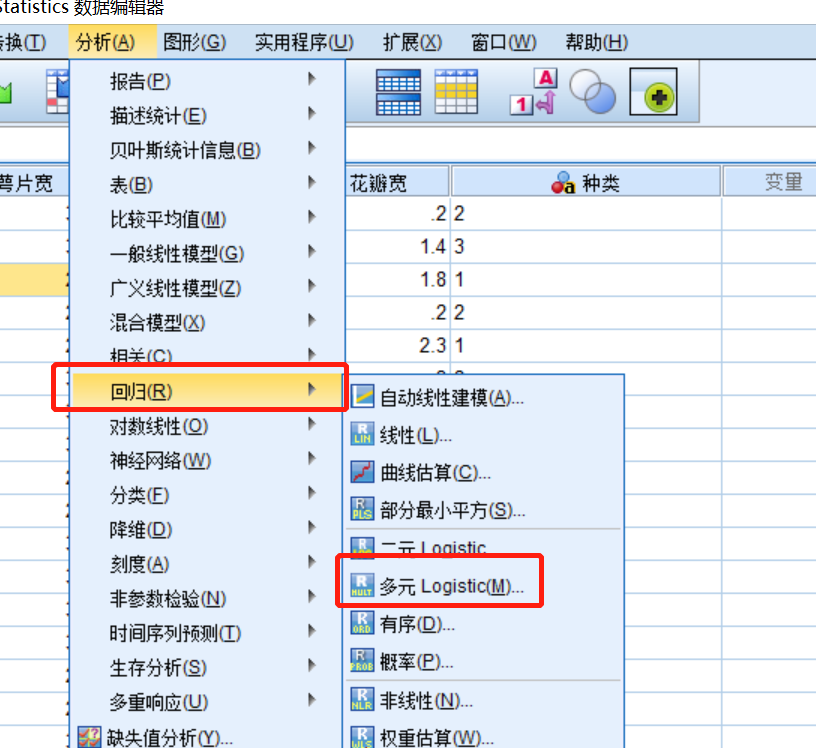
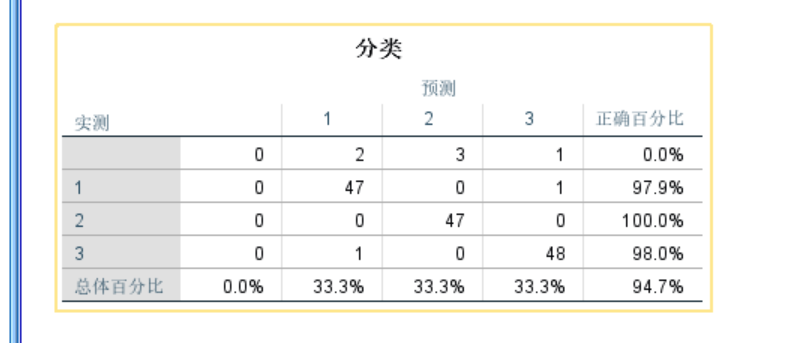
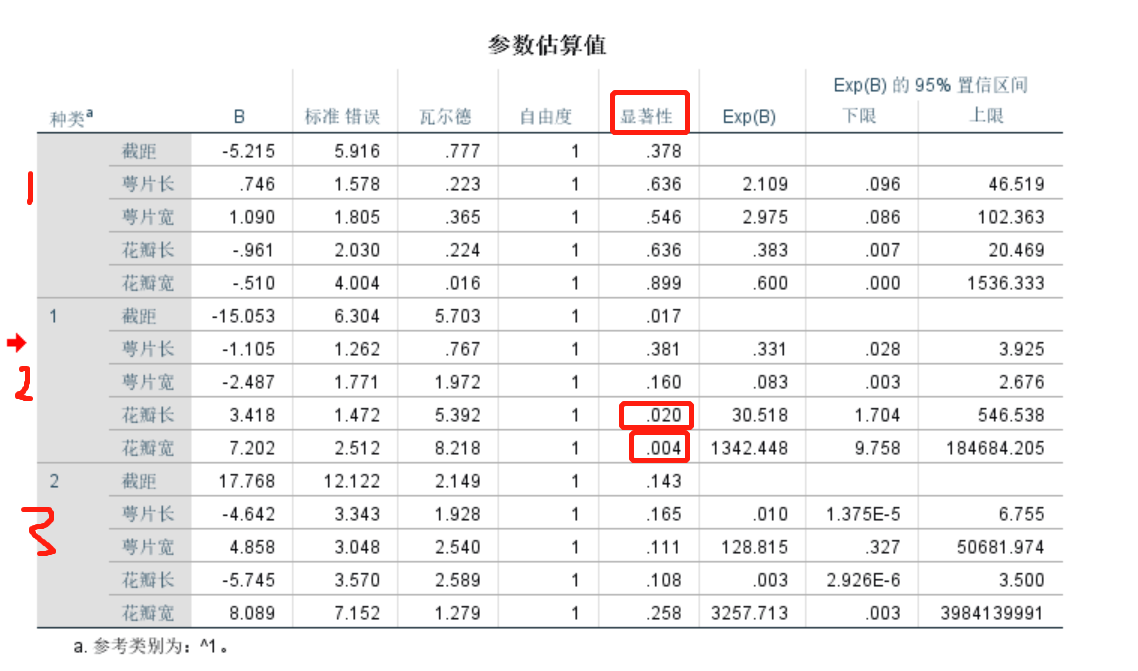
若是二分类,就如下系数表
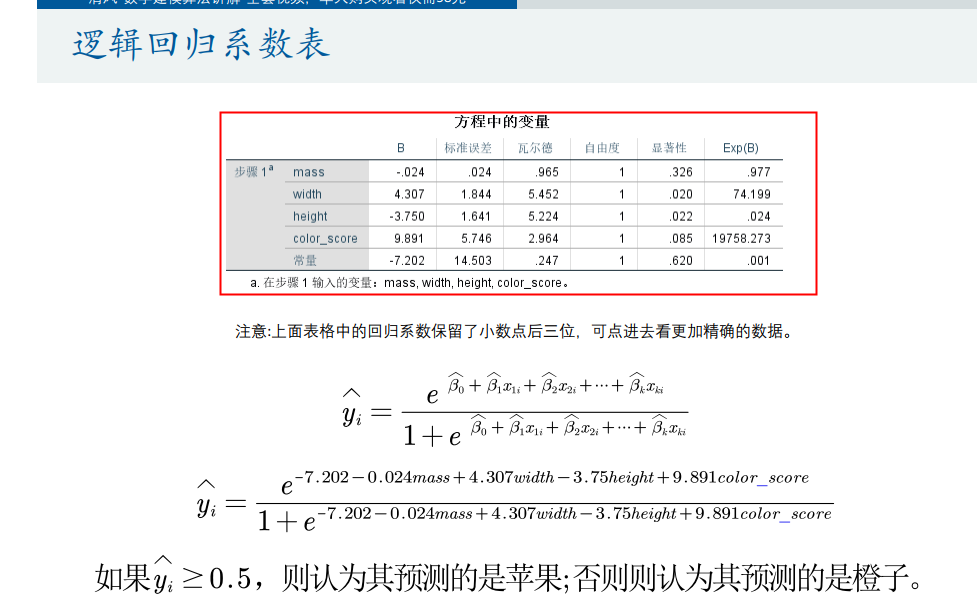
Fisher线性判别分析:
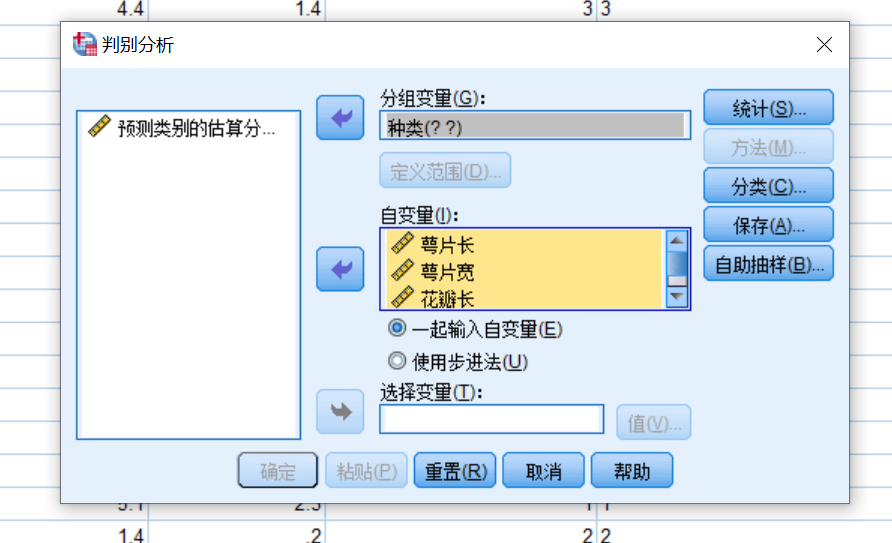
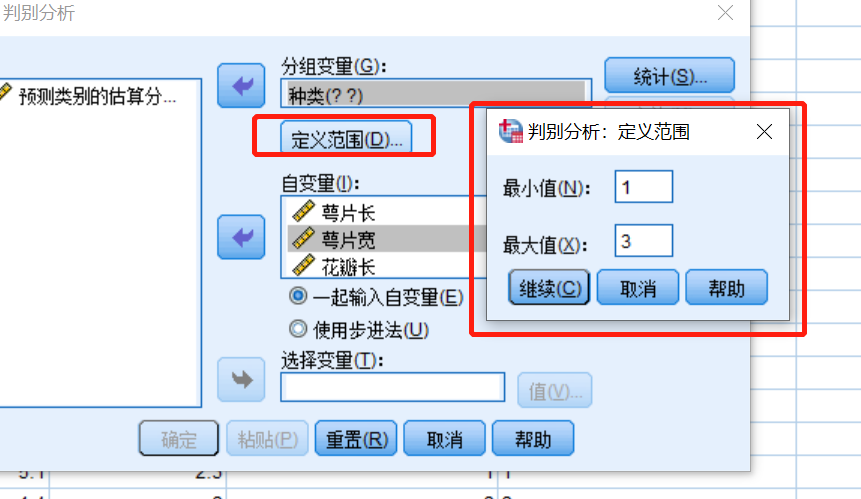
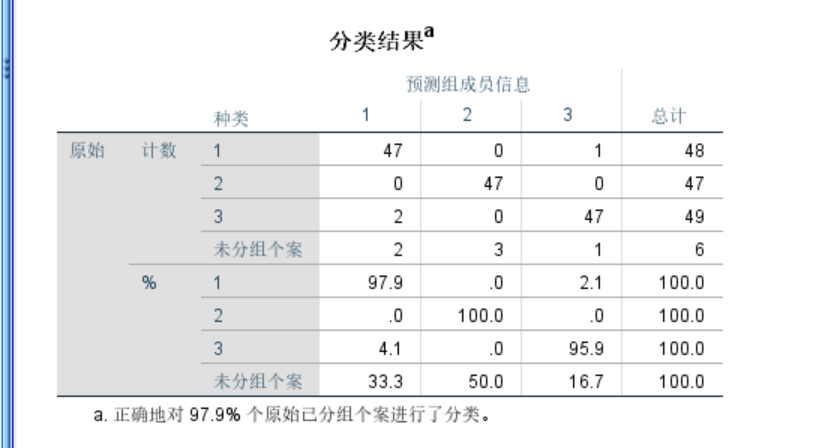
要分析的结果: