Module9 劳斯判据
1 稳定性判断
Method1:
step1:
解特征方程,求解出所有极点
step2:
a若没有一个极点在s平面右侧,则稳定;
b有一个在s平面右侧则不稳定;
c有极点在虚轴(有纯虚根),则响应趋于常数(实极点)或者等幅振荡(共轭复极点),也是不稳定
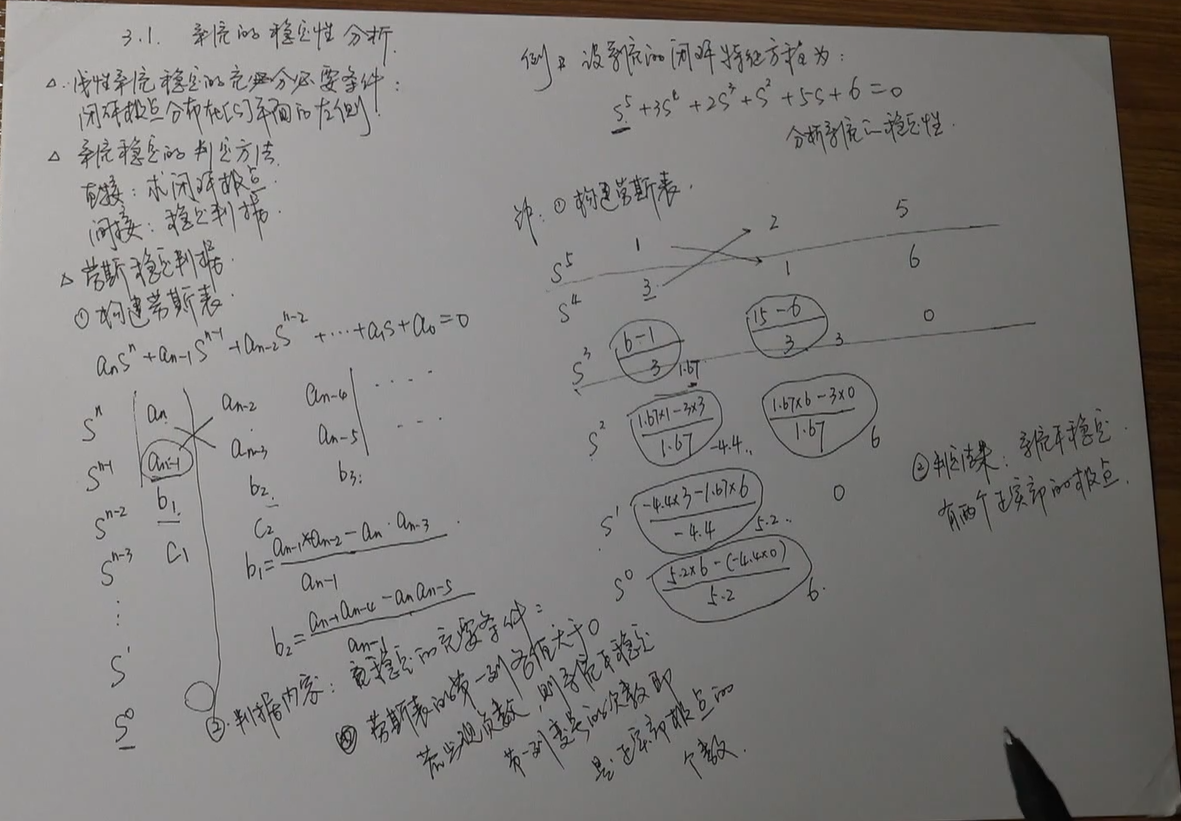
★★★Method2:劳斯判据


劳斯表:
前两行写特征方程系数,偶数个则刚好,奇数个最后不够的补0

example:
step1:系数均为正,无缺项
step2:列劳斯表
注意:不用写小数,分数判断正负即可


①可以按行约公因数:

②第一列出现0:用ε代替继续算劳斯表,最后取极限ε趋近于无穷小的整数(0.0001)

③整行为0:
step1:提上一行系数构造辅助方程,求导即为全0行系数
step2:判断第一列,有变号则不稳定
step3:无变号则解辅助方程,求出极点位置,由极点位置判断是否稳定(在虚轴老师说是不稳定)(技巧:辅助方程使用劳斯判据判断是否稳定,缺项就不稳定)



【小技巧】 在劳斯表第一列的最后一个元素,在不约分的情况下,等于方程的常数项,考试的时候可以验算自己有没有算错劳斯表。
约分时带来计算的简便,但验证还要在乘回去,在考试有计算器的情况下,并不能体现约分带来的方便,我认为不约分有利于验算
【注】出现全0行,说明极点在虚轴上
讲义