Module7 高阶系统
★1 高阶系统的处理方法
method: Reduction(降为二阶)
condition:(两个极点离虚轴的距离相差十倍以上)
attention: 化成Bode form再舍弃非主导极点(一般为实极点)
★2 三阶系统实例分析
2.1 实极点的作用

实极点的作用:make reponse sluggish(迟缓)(阻力),越靠近虚轴越有阻力作用
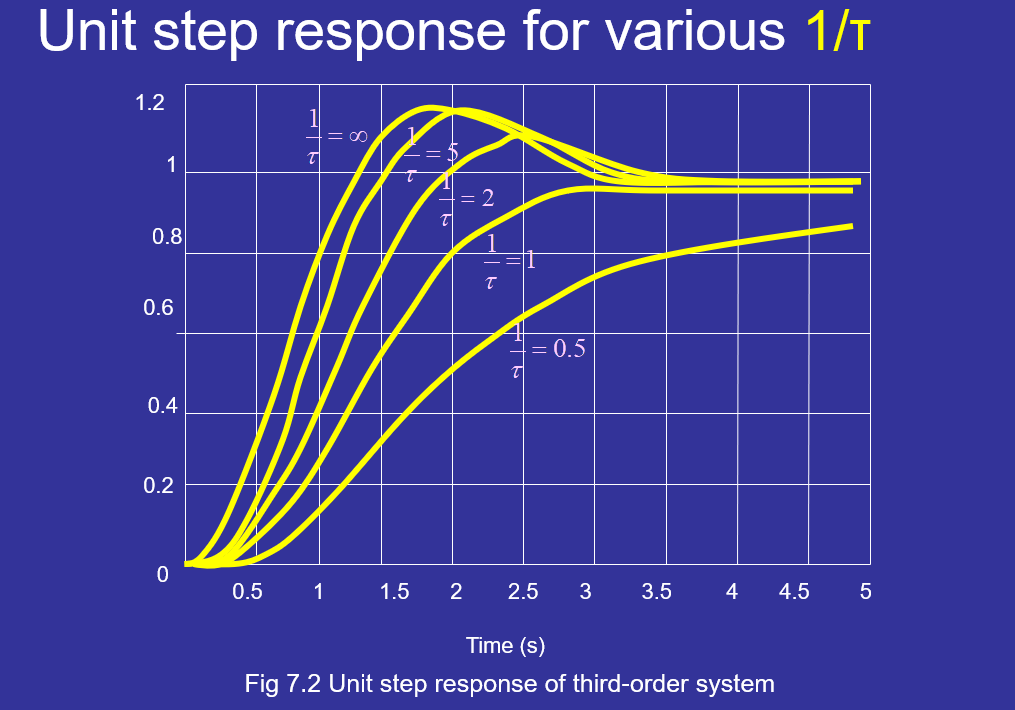
2.2 极点的影响
定义一个参数:
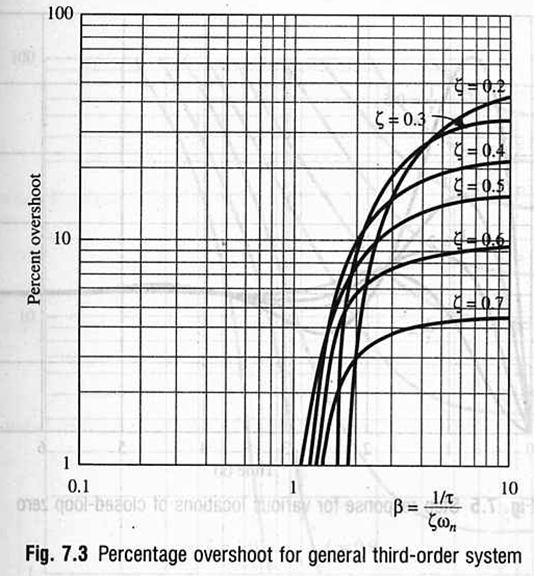
★★★结论:
- β>=10,便可降为二阶系统,实极点未发挥【阻力】的作用,响应的超调满足二阶系统PO与ζ的关系图
- β<=1,实极点发挥【阻力】的作用,响应不再有【超调】
- β<=0.1,降为一阶系统
- 1<β<10,三阶系统不能直接降阶,要考虑实极点【阻力】的作用,根据上图中由不同的ζ来确定PO,以此来做题画图
2.3 零点的作用
例子:二阶系统零点的影响 实零点的作用:make reponse more-oscillatory(振荡)(动力),越靠近虚轴越有动力作用
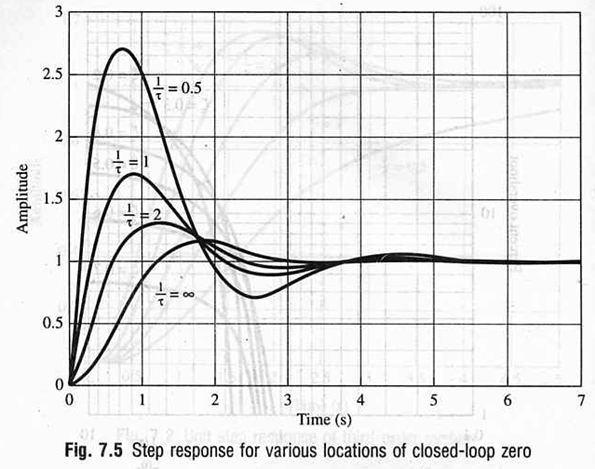
2.4 零点的影响
定义一个参数:
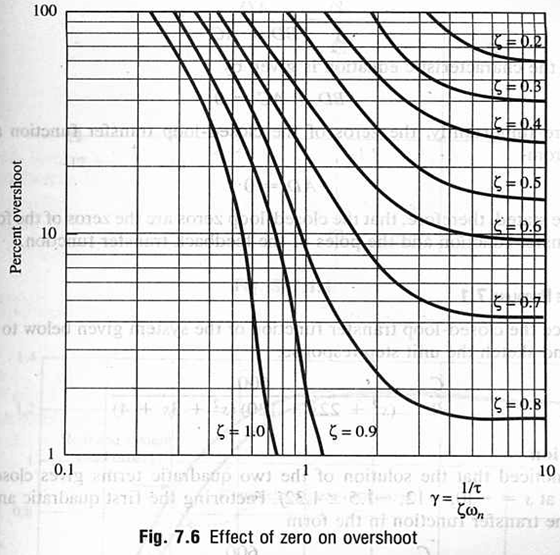
★★★结论:
- γ>=10,,实零点未发挥【动力】的作用,响应的超调满足二阶系统PO与ζ的关系图
- γ<10,要考虑实零点【动力】的作用,根据上图中由不同的ζ来确定PO,以此来做题画图
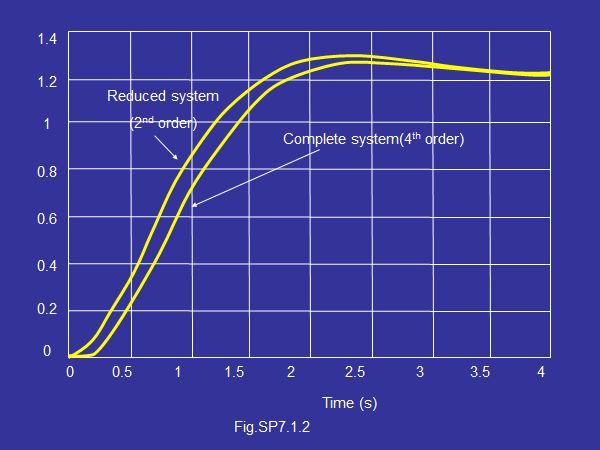
3 sample problem 7.1
给如下四阶系统降阶:
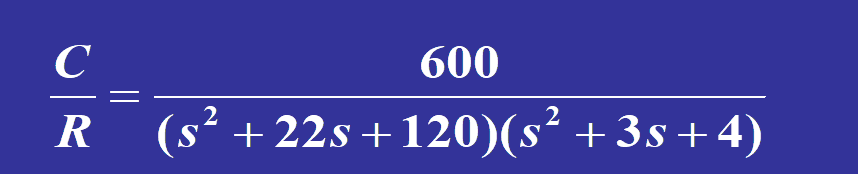



matlab验证: