《自控原理》 Module12 频率特性

对于核反应堆控制系统，要判断稳定性，但是闭环传函/开环传函难以求解！所以我们通过看open-loop frequency response来判断稳定性。

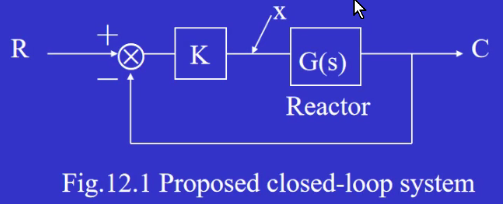
频率响应即输入一个正弦信号；发现正弦输入和输出的“频率”相同，输出的“幅值”和“相位“是“频率”的函数。

由开环传函求频率响应：令s=jω；问题：与上面核反应堆例子说的是否矛盾？不知道传函，这里又是由传函求频率响应。对应关系是确定的；先通过已知传函得到一些结论，再通过结论反推未知传函

总结：

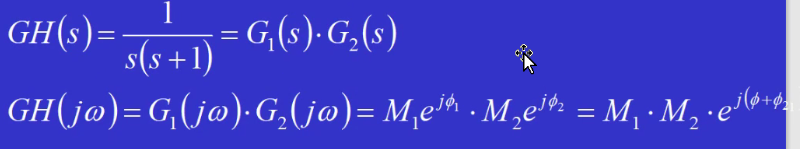
起点：除了积分环节，起点都是(1,0)；积分环节起点是∞，趋近方向为-90*n(n是积分的阶数)

终点：除了微分环节，终点都是原点，趋近方向为(n-m)*(-90) (n=分母s的阶数，m=分子s的阶数)

时域分析的出发点是“闭环传函”，频域分析的出发点是“开环传函GH”，a generalized open-loop transfer function：

有六个环节，从左到右从上到下依次为：比例环节，一阶微分；二阶微分；积分环节；惯性环节；震荡环节

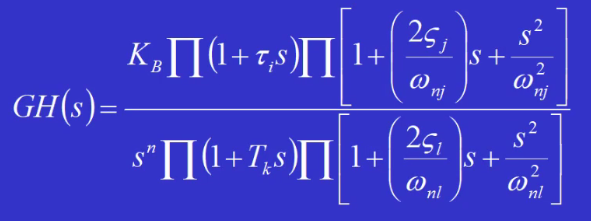
画奈奎斯特图如下(考试不考)

比例环节是一个点

惯性环节(ω:0>+∞)是以0到1为直径的半圆

一阶微分环节

积分环节(与型有关)

震荡环节

二阶微分

总结：

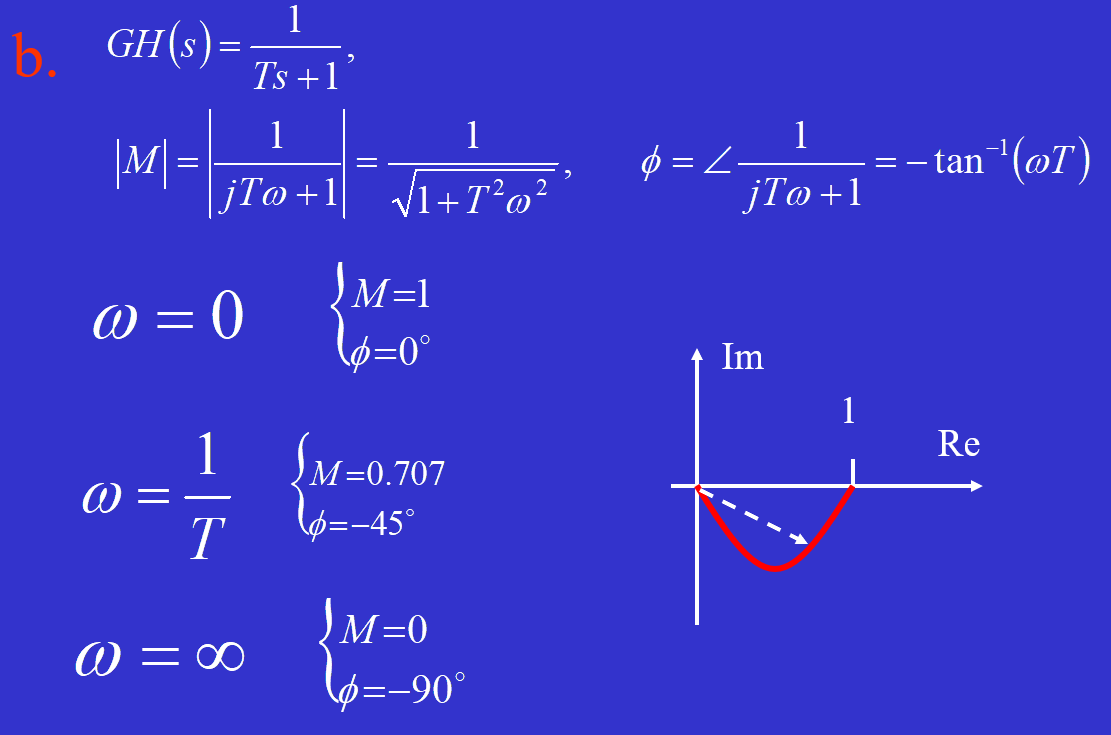
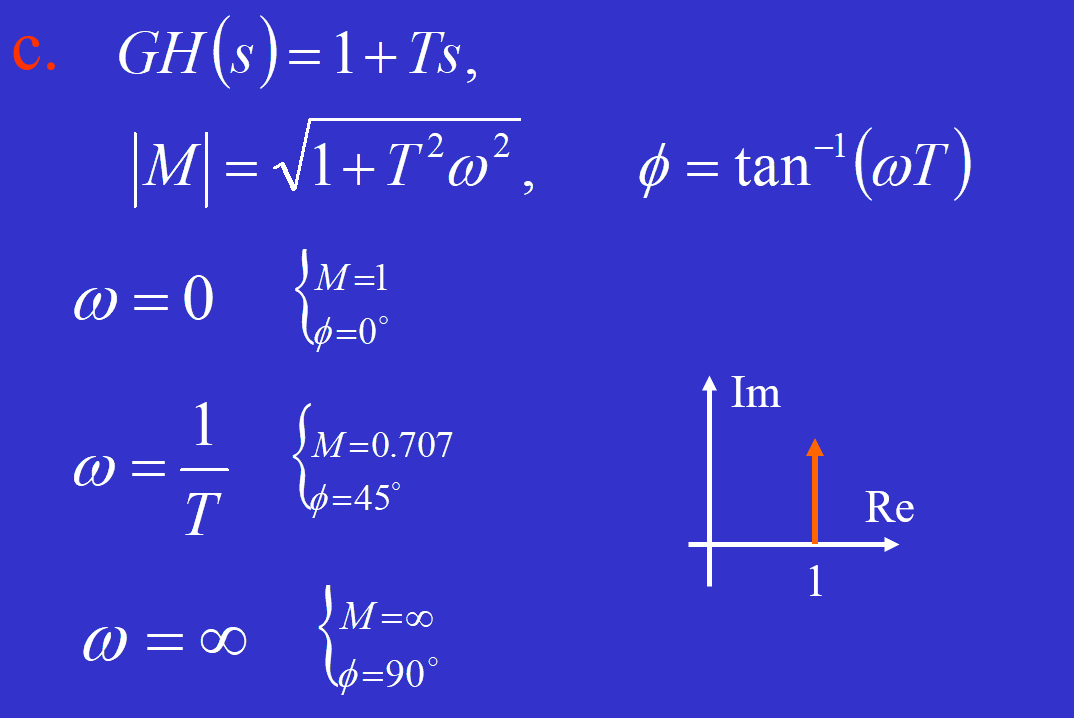
起点：除了积分环节，起点都是(1,0)；积分环节起点是∞，趋近方向为-90*n(n是积分的阶数)

终点：除了微分环节，终点都是原点，趋近方向为(n-m)*(-90) (n=分母s的阶数，m=分子s的阶数)

做题总结：

先将开环传递函数化为标准形式(Bode form)

王老师讲义

什么是“频率特性”： 若系统的传递函数为G(s)，令s=jω，则G(jω)就称为系统的频率特性

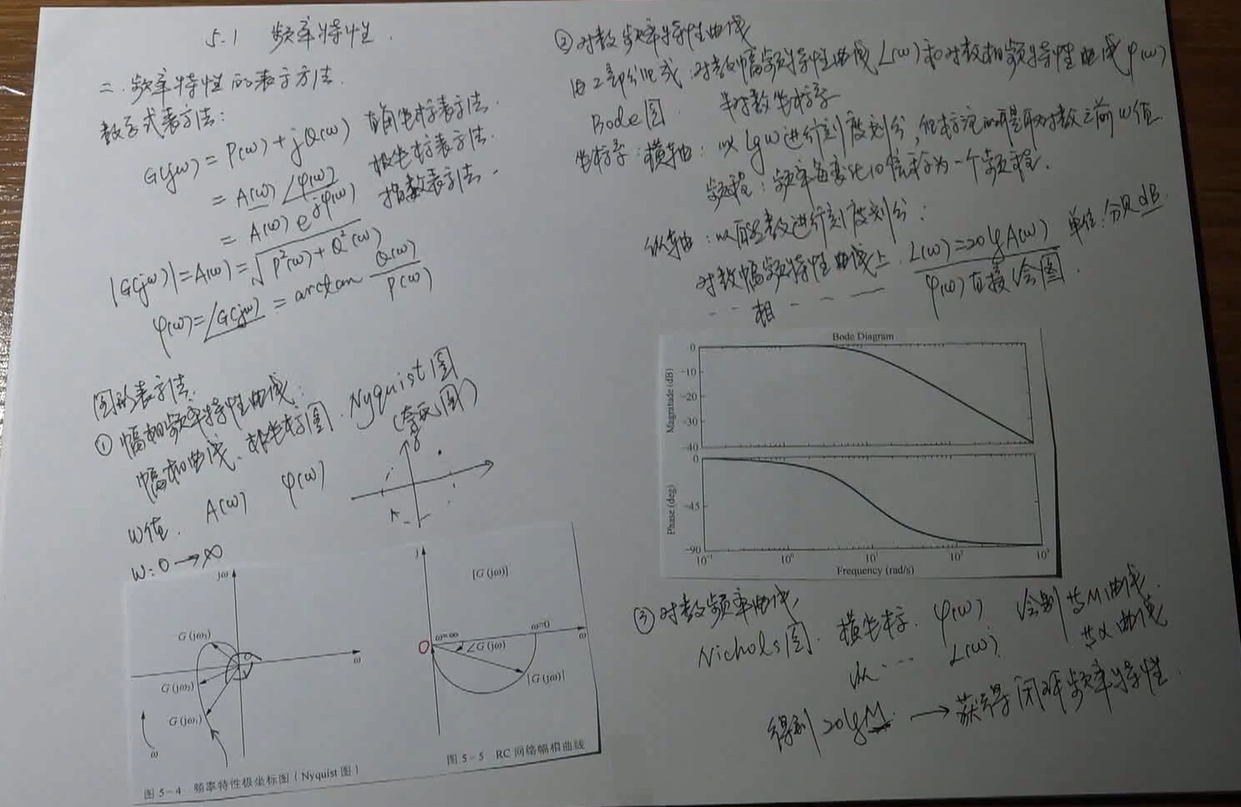
绘制方法