平衡⼆叉树(AVL树)
定义
平衡⼆叉树(Self-BalancingBinarySearchTree或Height-BalancedBinarySearchTree),是⼀种⼆叉排序树.其中每⼀个结点的左⼦树和右⼦树的⾼度差⾄多等于1.
两位俄罗斯数学家G.M.Adelson-Velskii和E.M.Landis共同发明的⼀种解决平衡⼆叉树的算法.也称为AVL树
⾼度平衡:意思是说,要么它是⼀颗空树,要么它的左⼦树和右⼦树都是平衡⼆叉树.且左⼦树和右⼦树的深度之差的绝对值不超过1;我们将⼆叉树上结点的左⼦树深度减去右⼦树深度的值称为平衡因⼦BF(BalanceFactr)
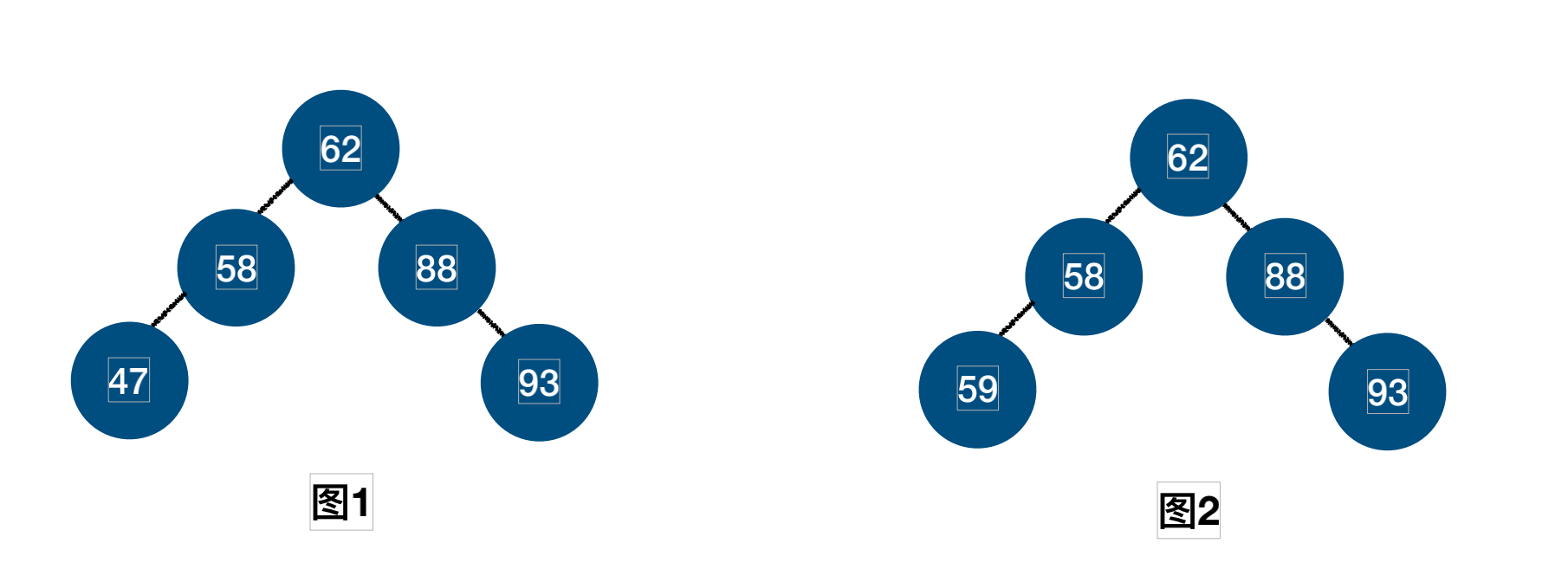
图1是平衡二叉树,因为左子树减去右子树为0,而图2,59>58,59却放在左边,不是一个二叉排序树,自然不是平衡二叉树。
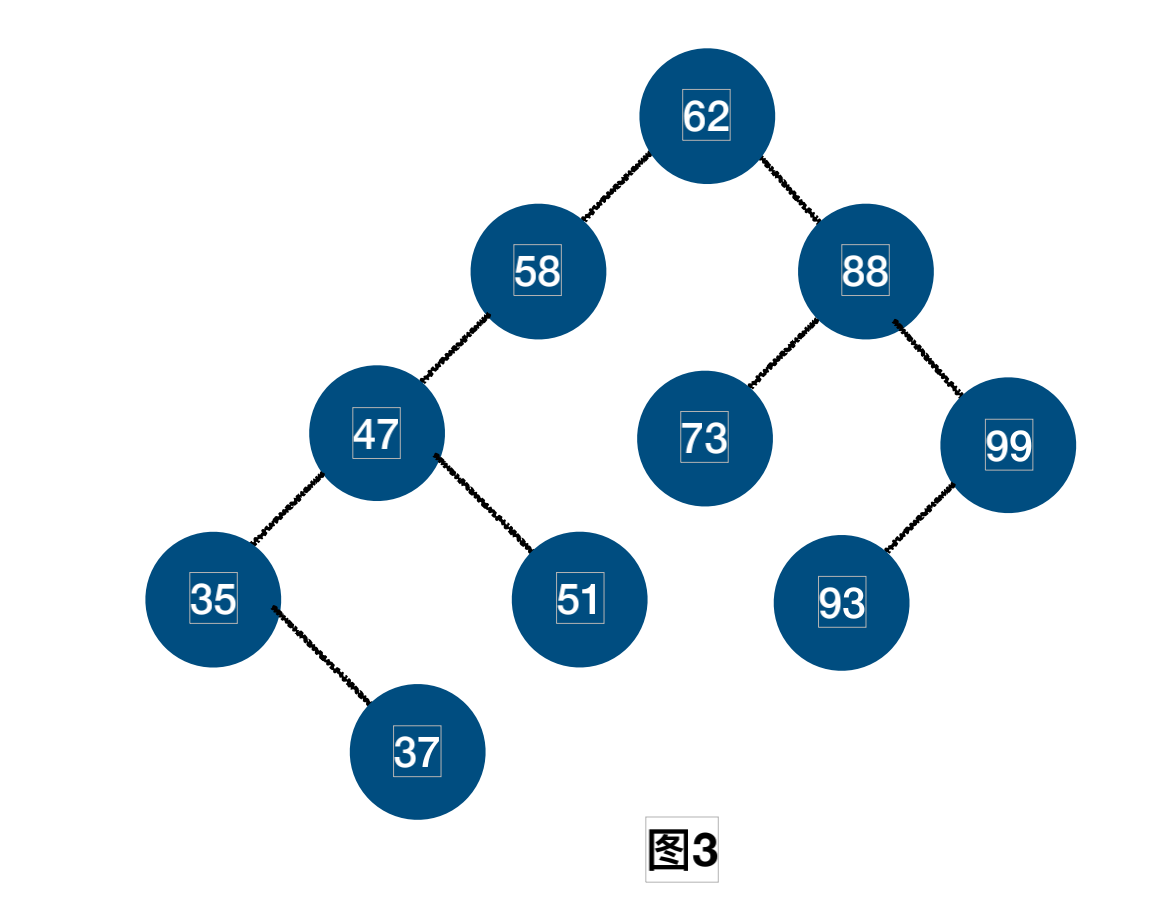
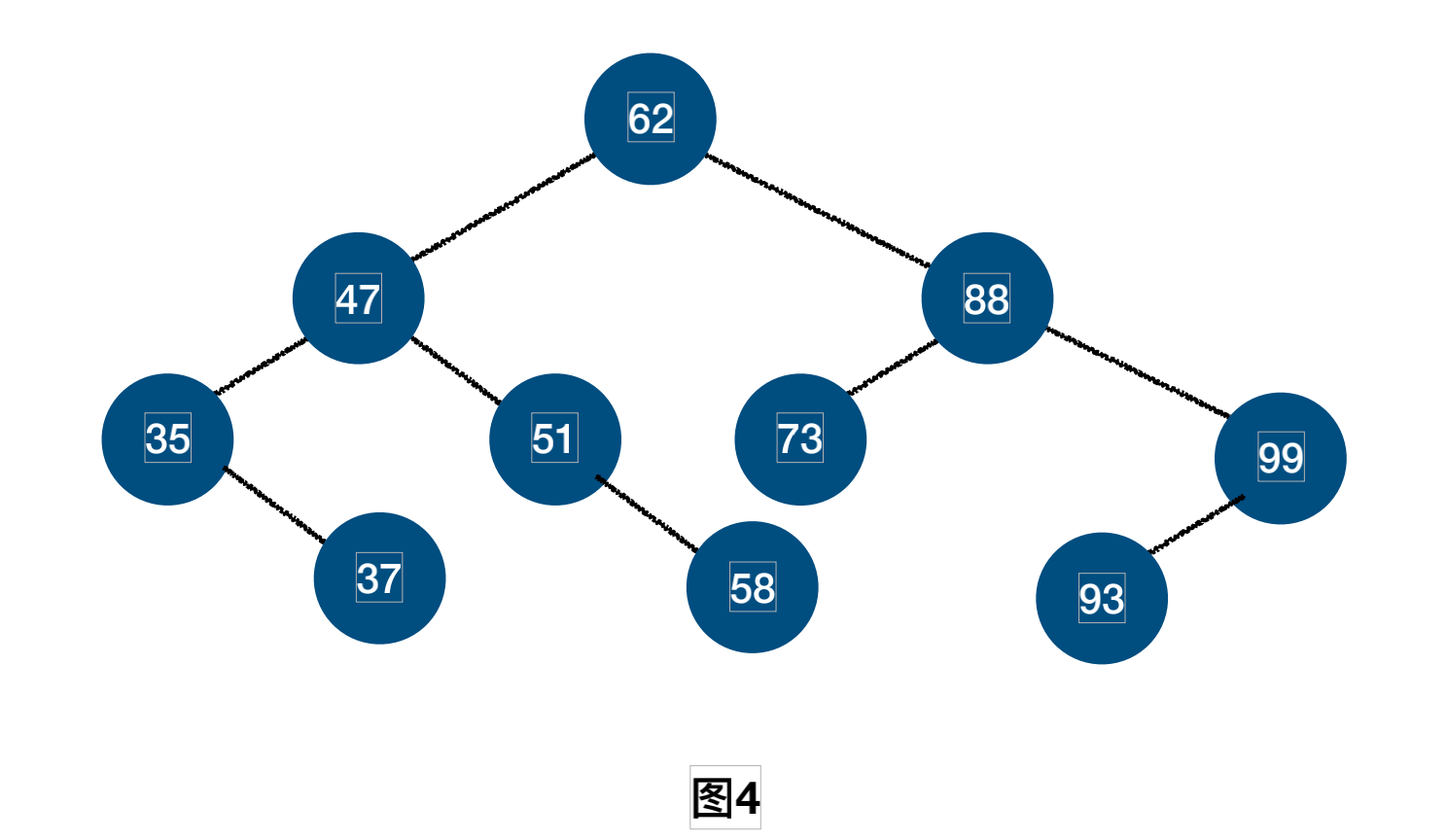
图3不是平衡二叉树,图4是二叉树
最⼩不平衡⼦树
定义:距离插⼊点最近的,且平衡因⼦的绝对值⼤于1的结点为根的⼦树,我们称为最⼩不平衡⼦树
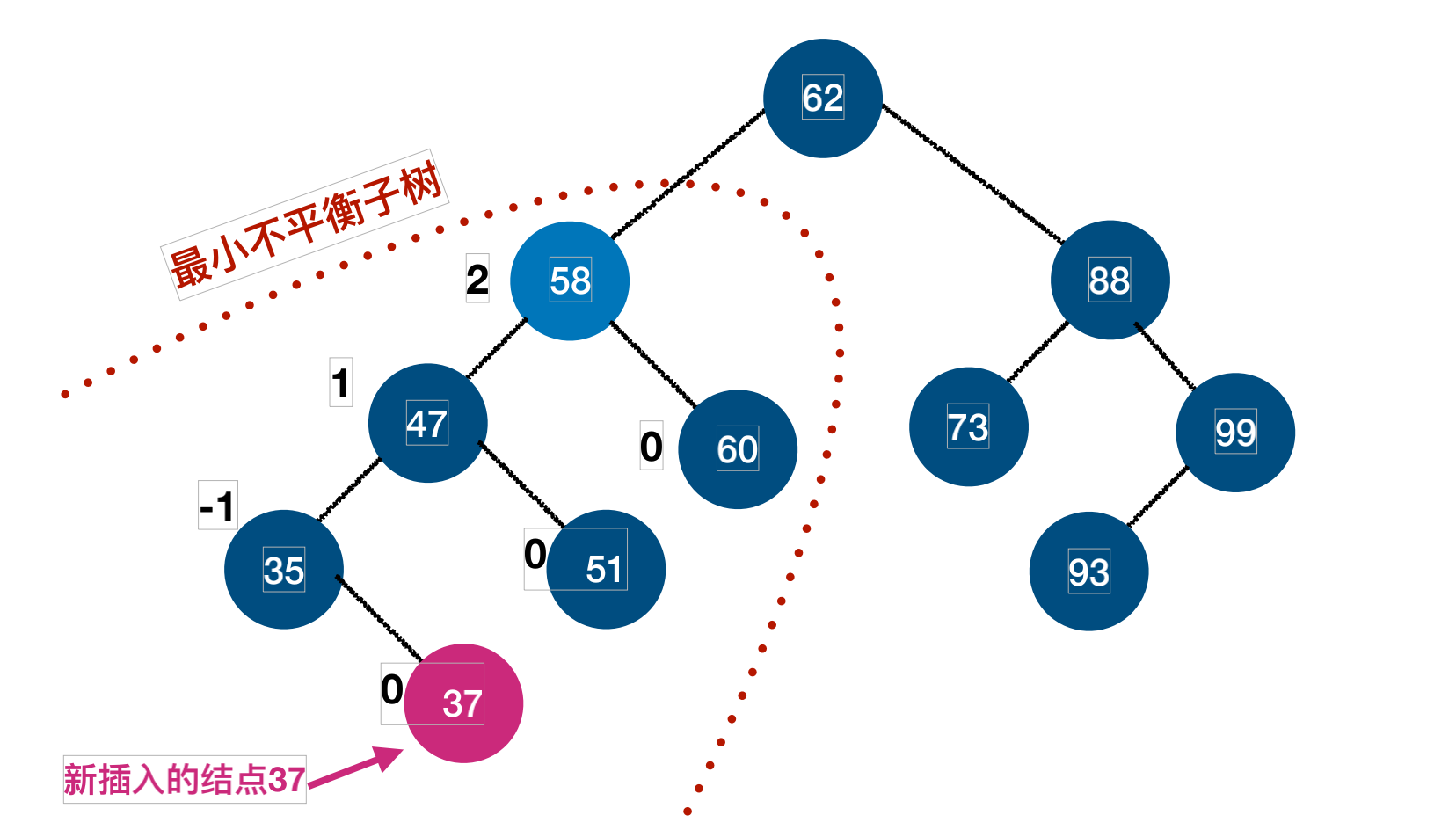
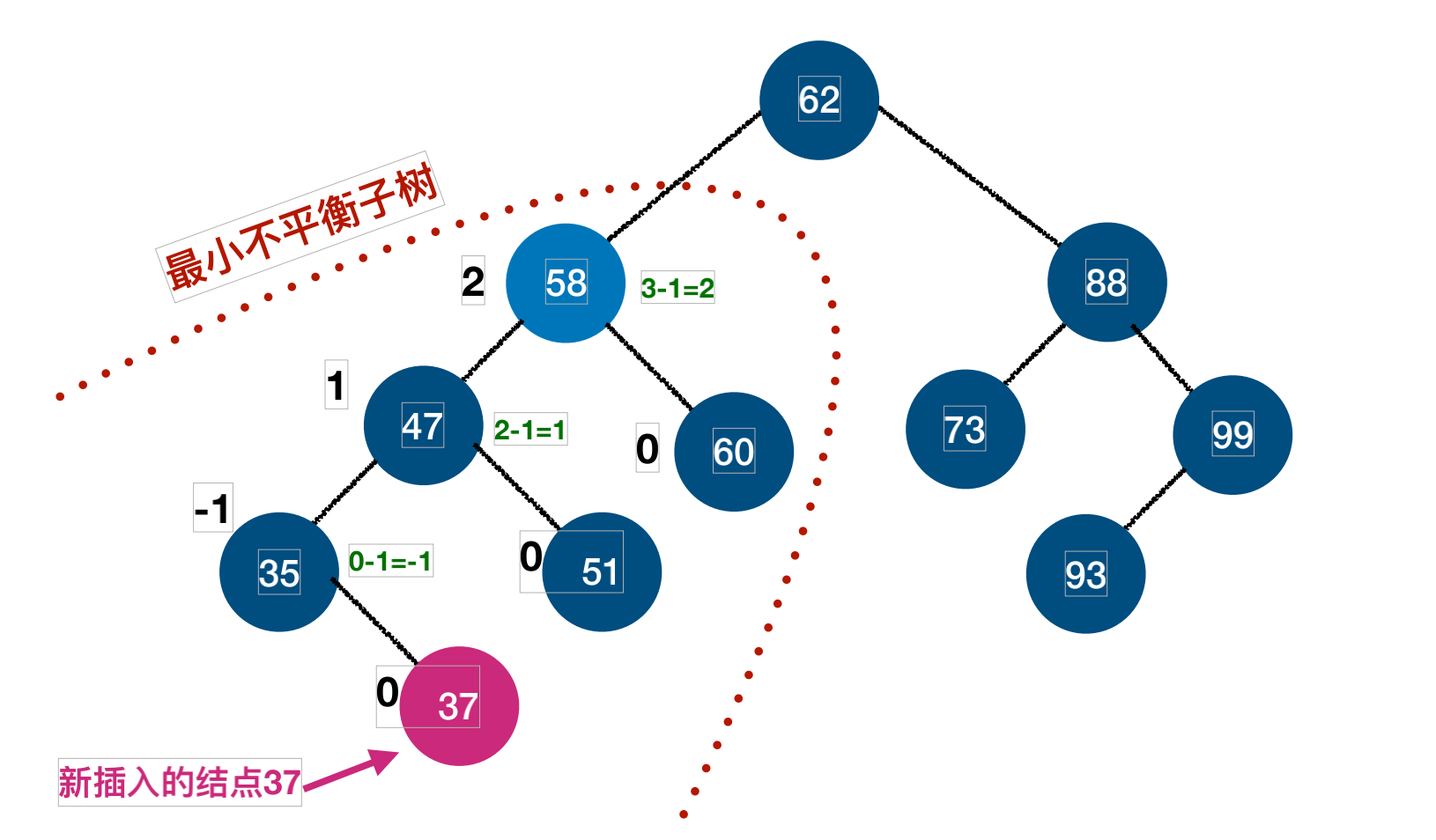
平衡⼆叉树构建的基本思想
在构建⼆叉排序树的过程中,每当插⼊⼀个结点时,先检查是否因插⼊⽽破坏了树的平衡性.若是,则找到最⼩不平衡⼦树.在保持⼆叉排序树特性的前提下,调整最⼩不平衡⼦树中各结点之间的链接关系.进⾏相应的旋转,使之成为新的平衡⼦树.
平衡⼆叉树构建模拟
数组a[10]={3,2,1,4,5,6,7,10,9,8}需要构建⼆叉排序树.
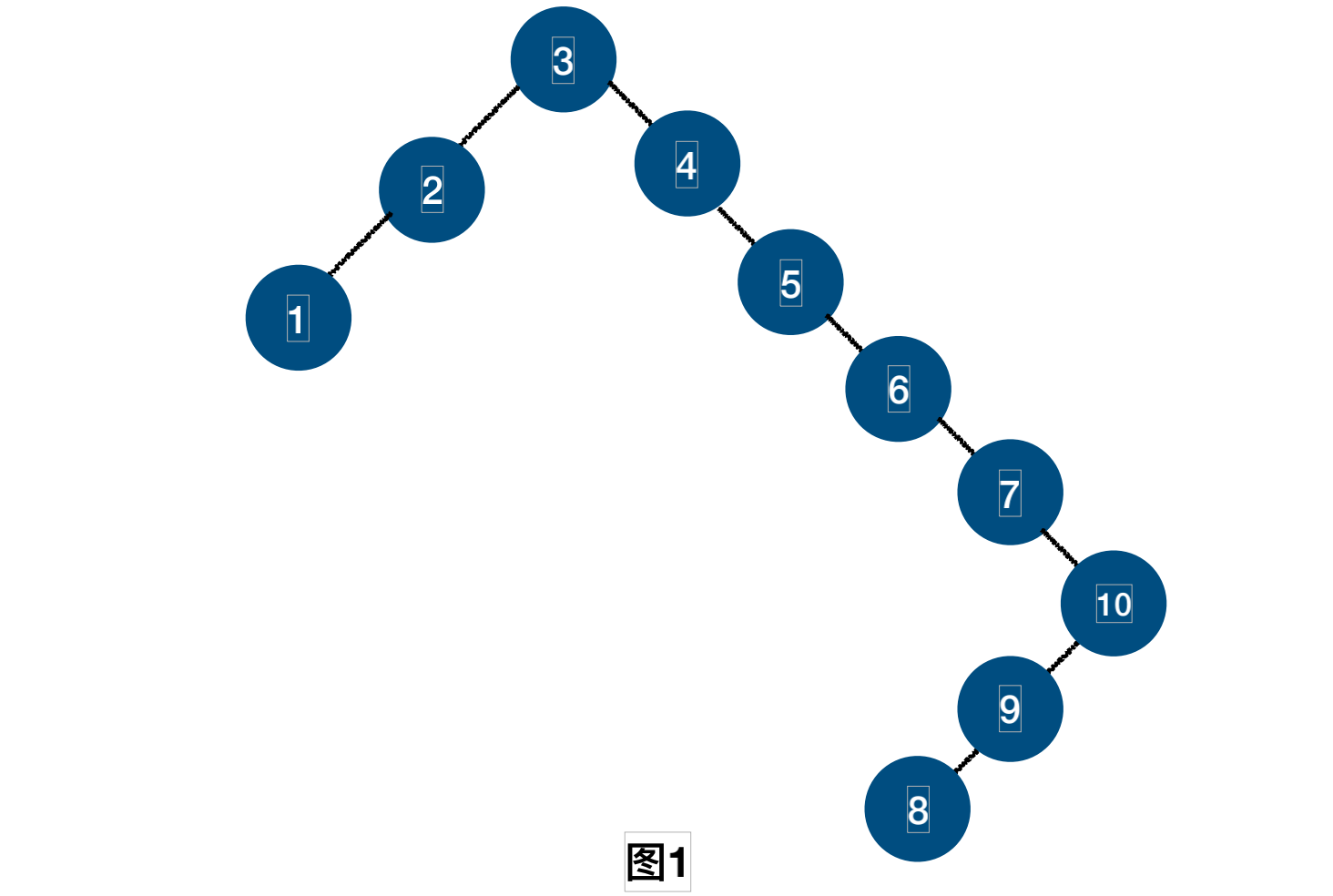
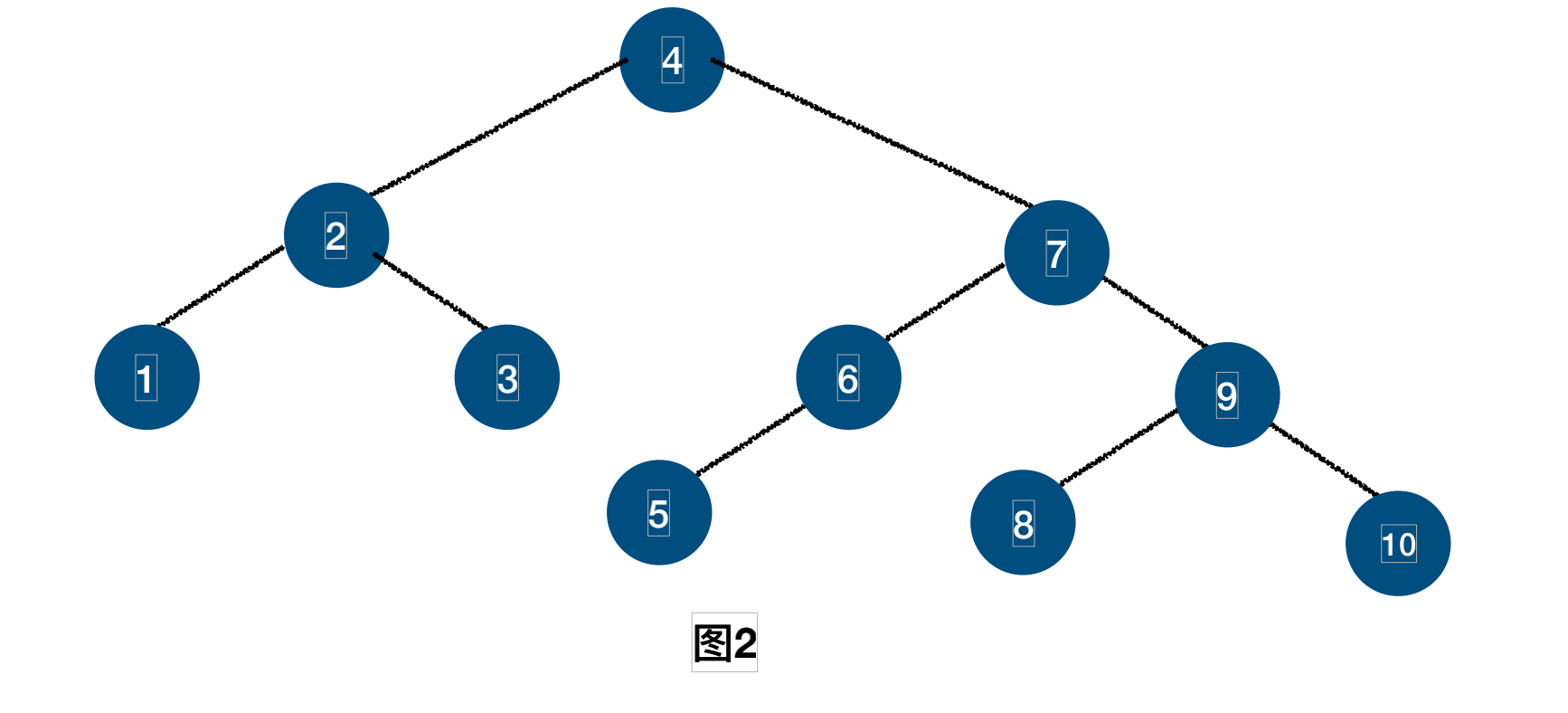
我们会发现图2比图1的查找更高效,深度变得更浅更容易查找。
插⼊结点3,2,1的过程:
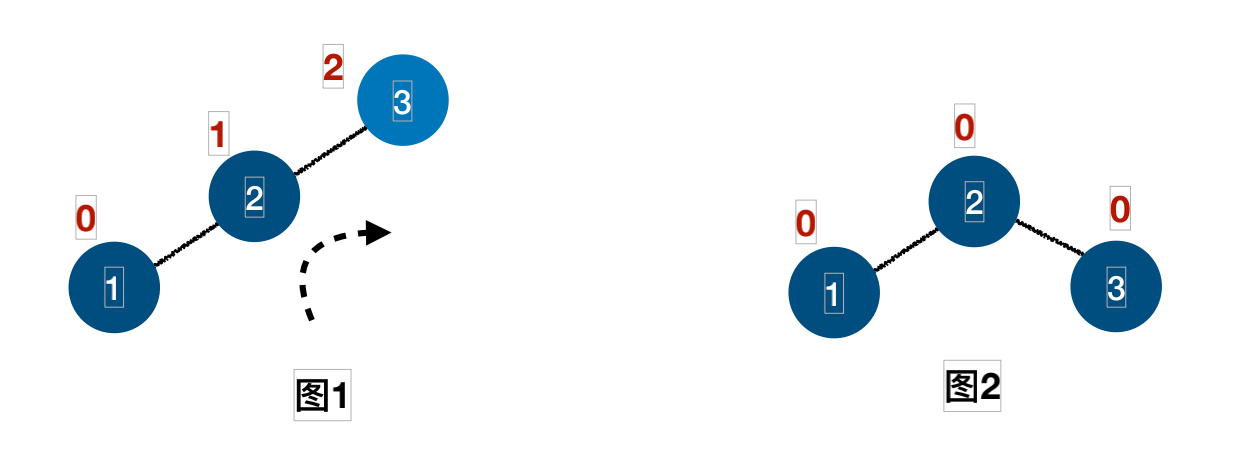
插⼊结点4的过程:
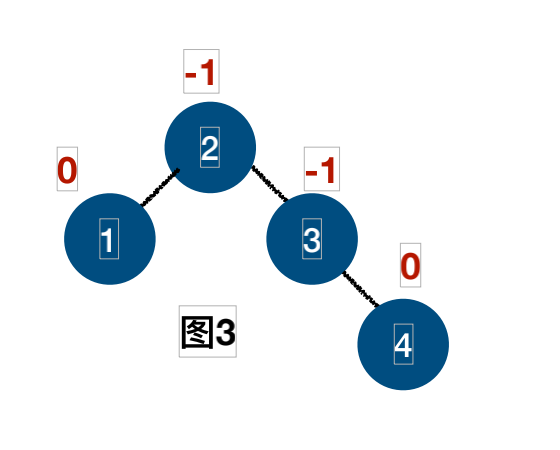
插⼊结点5的过程:
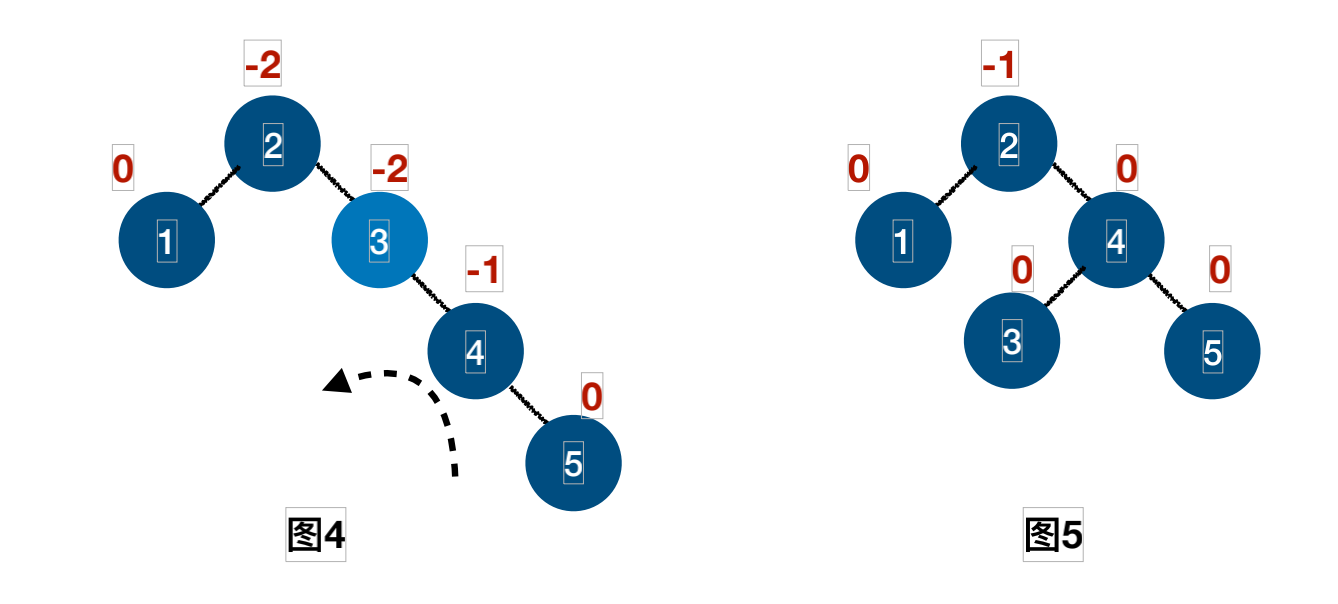
插⼊结点6的过程:
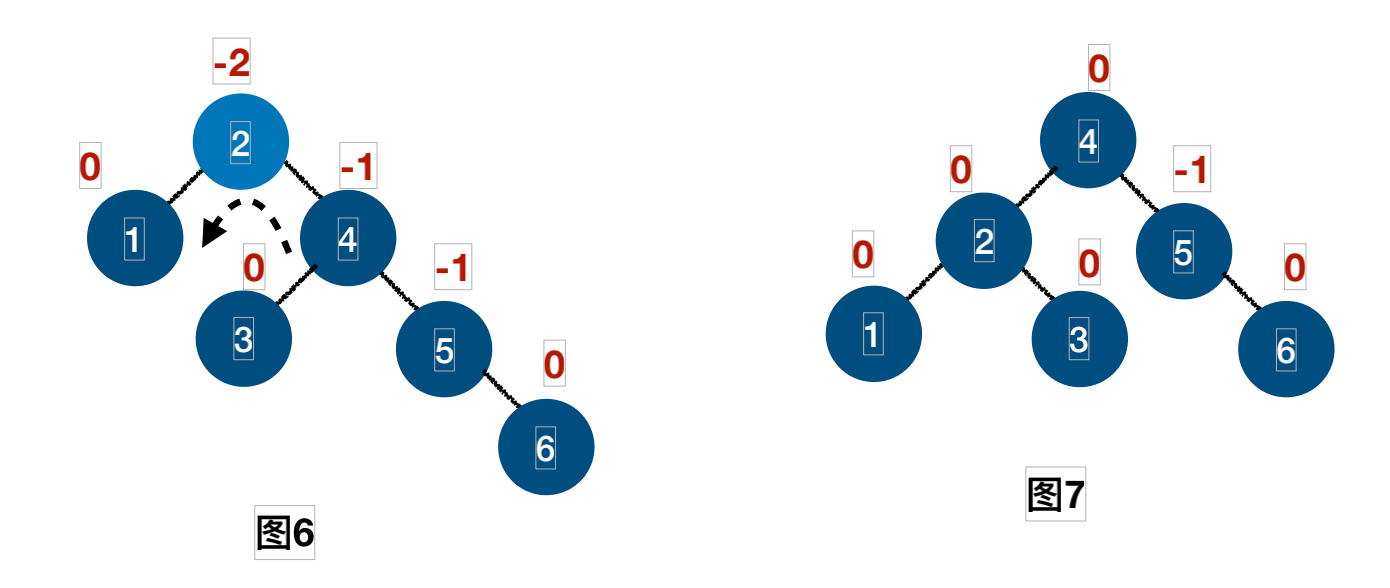
插⼊结点7的过程:
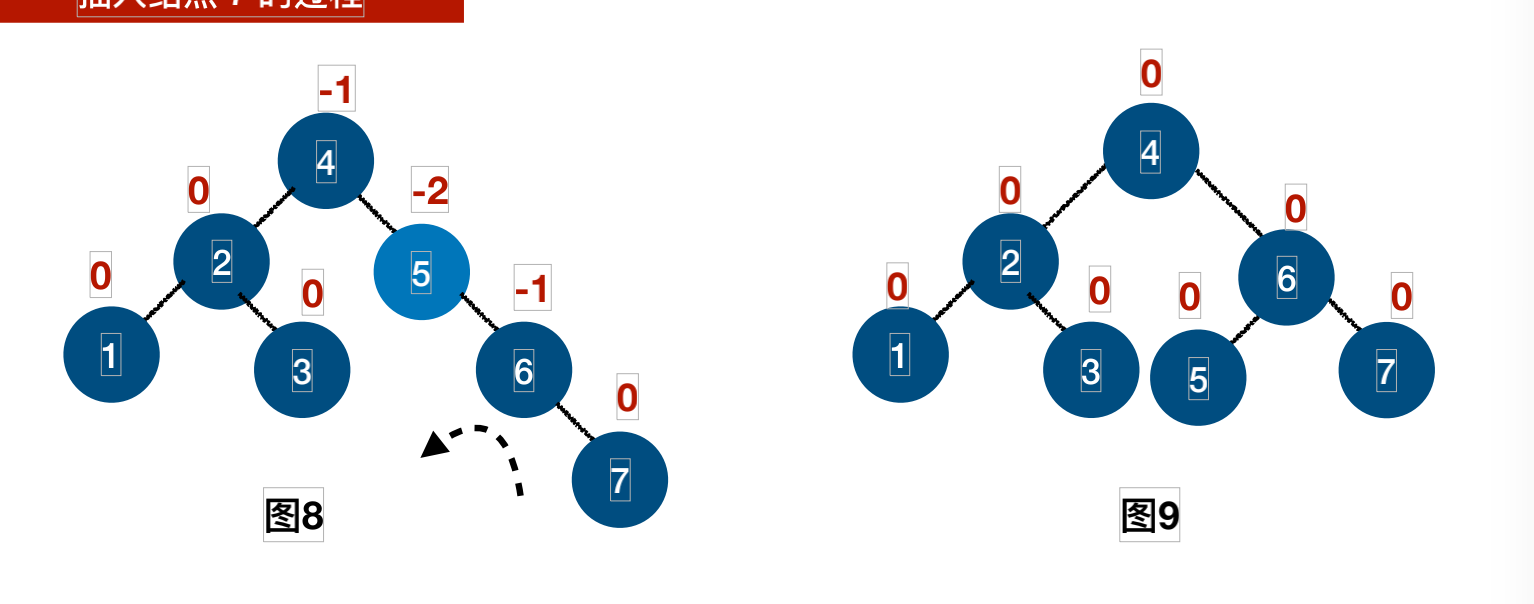
插⼊结点8的过程:
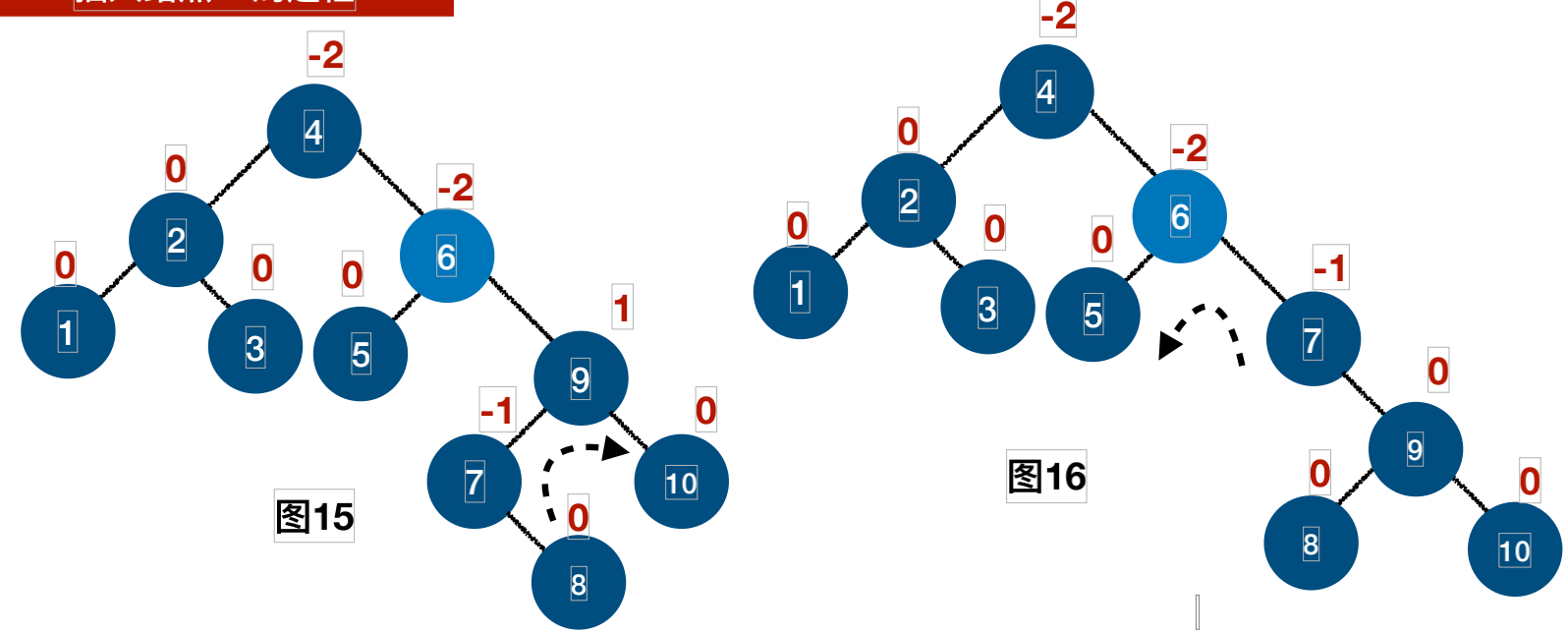
插⼊结点9的过程:
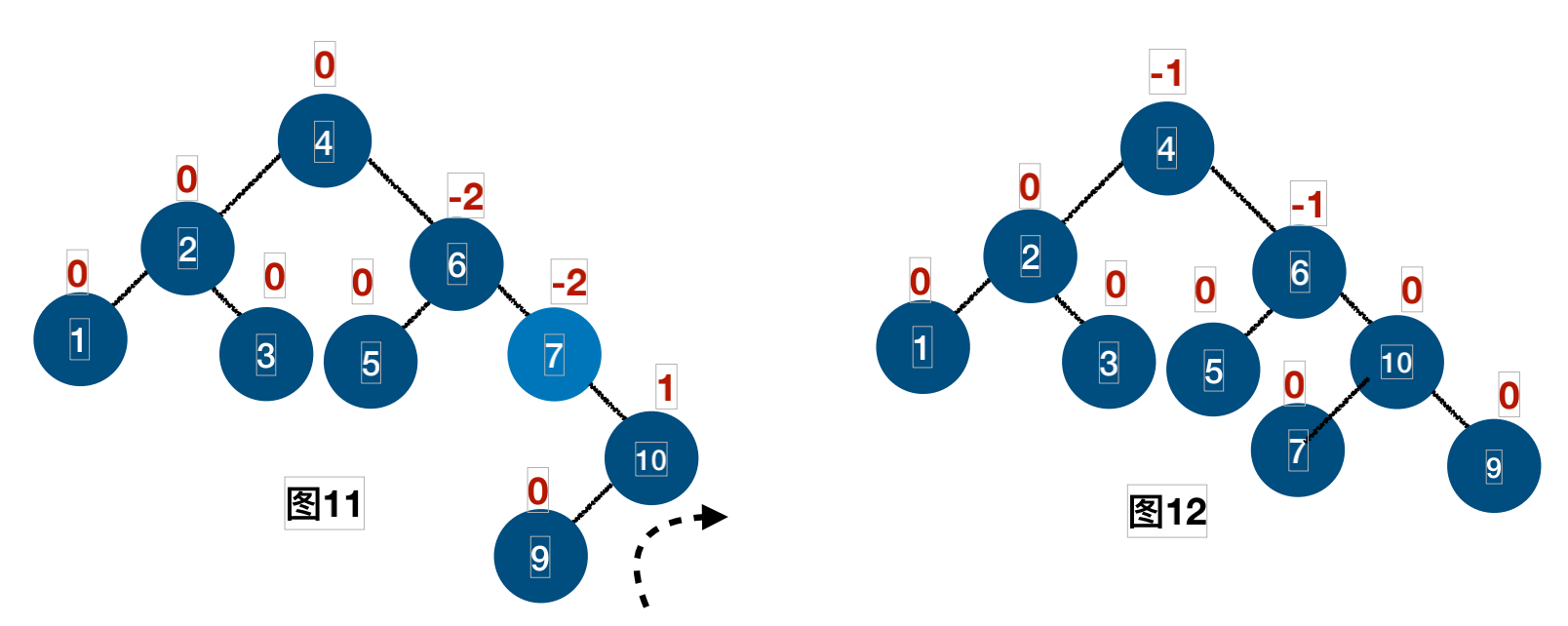
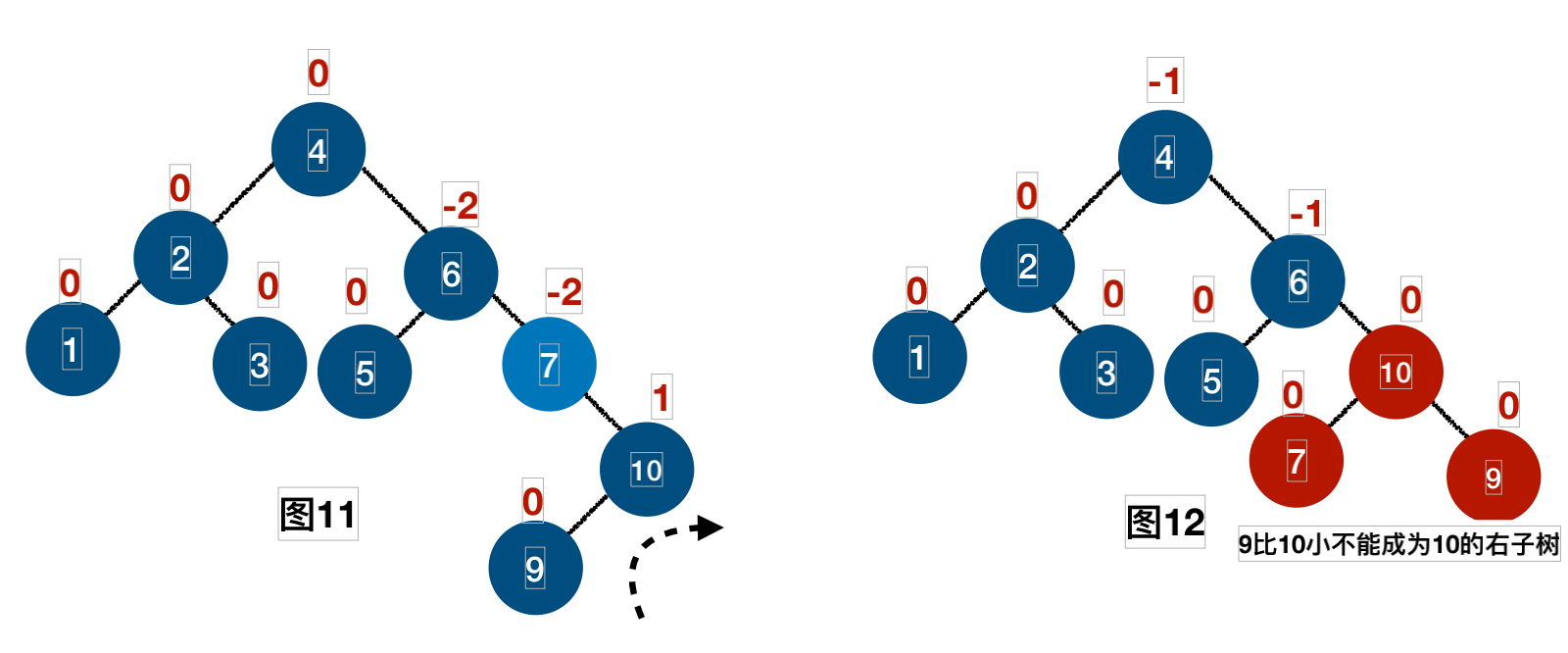
插⼊结点10的过程:
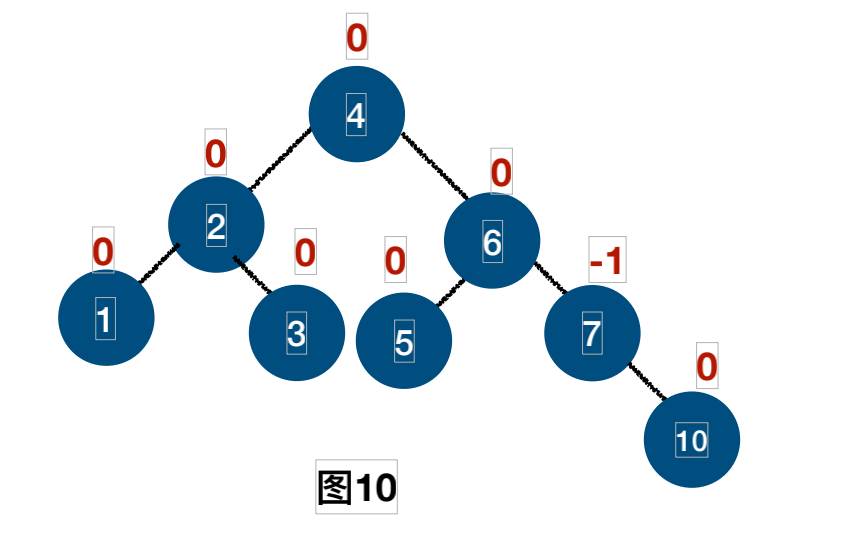
平衡⼆叉树结点结构设计
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100
typedef int Status;
//结点结构typedef struct BiTNode{
//结点数据
int data;
//结点的平衡因子
int bf;
//结点左右孩子指针
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
右旋:
- P做为右旋的根结点;
- L的右⼦树成为了P的左⼦树;
- P成为了L的右⼦树;
- L替换了P,成为⼆叉排序树新的根结点
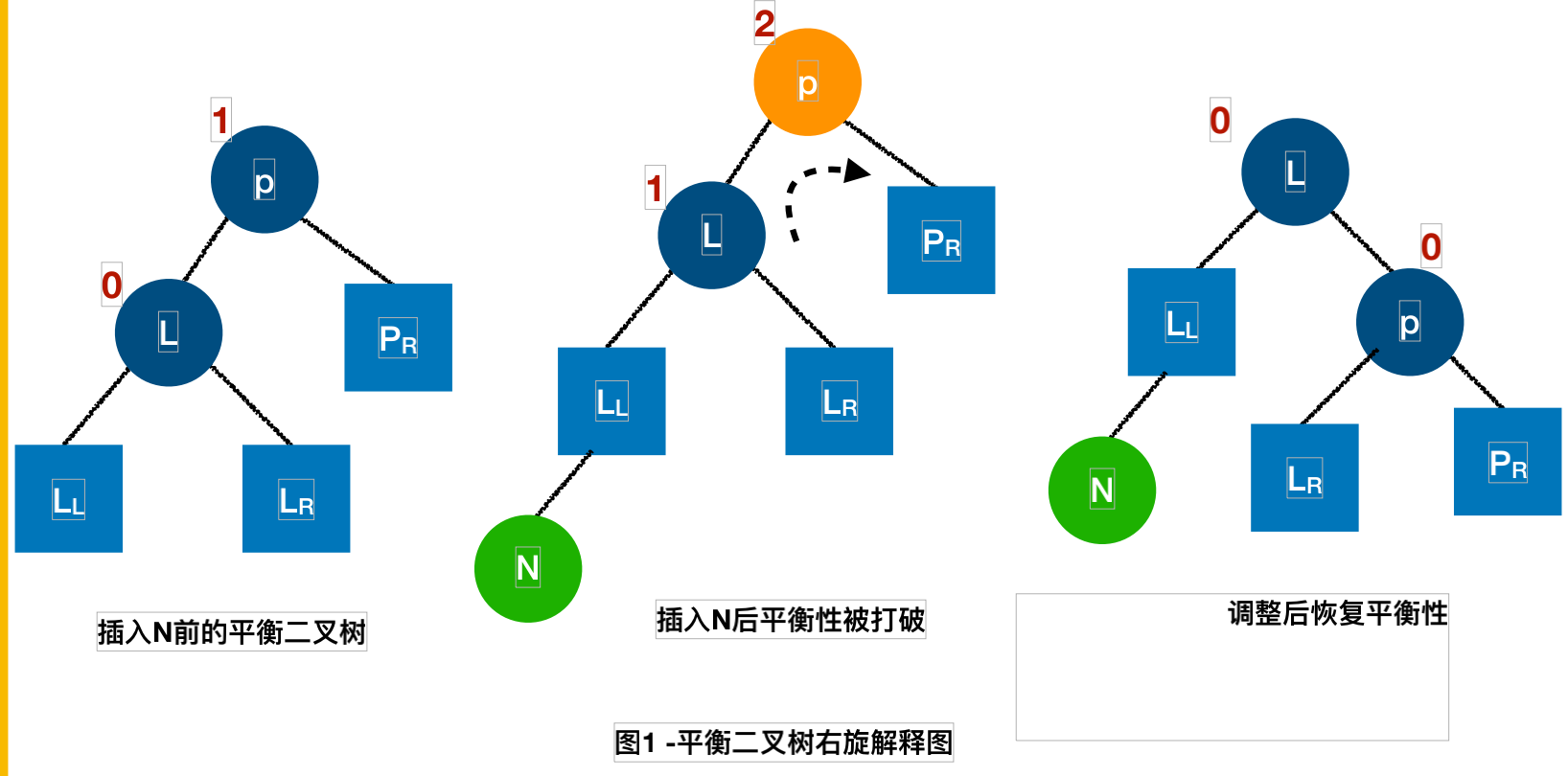
/* 对以p为根的二叉排序树作右旋处理; 处理之后p指向新的树根结点,即旋转处理之前的左子树的根结点; */void R_Rotate(BiTree *p){ BiTree L; //① L是p的左子树;
L = (*p)->lchild;
//② L的右子树作为p的左子树
(*p)->lchild = L->rchild;
//③ 将p作为L的右子树
L->rchild = (*p);
//④ 将L替换原有p的根结点位置
*p = L;
}
左旋:
- P做为左旋的根结点;
- R的左⼦树成为了P的右⼦树;
- P成为了R的左⼦树;
- R替换了P,成为⼆叉排序树新的根结点
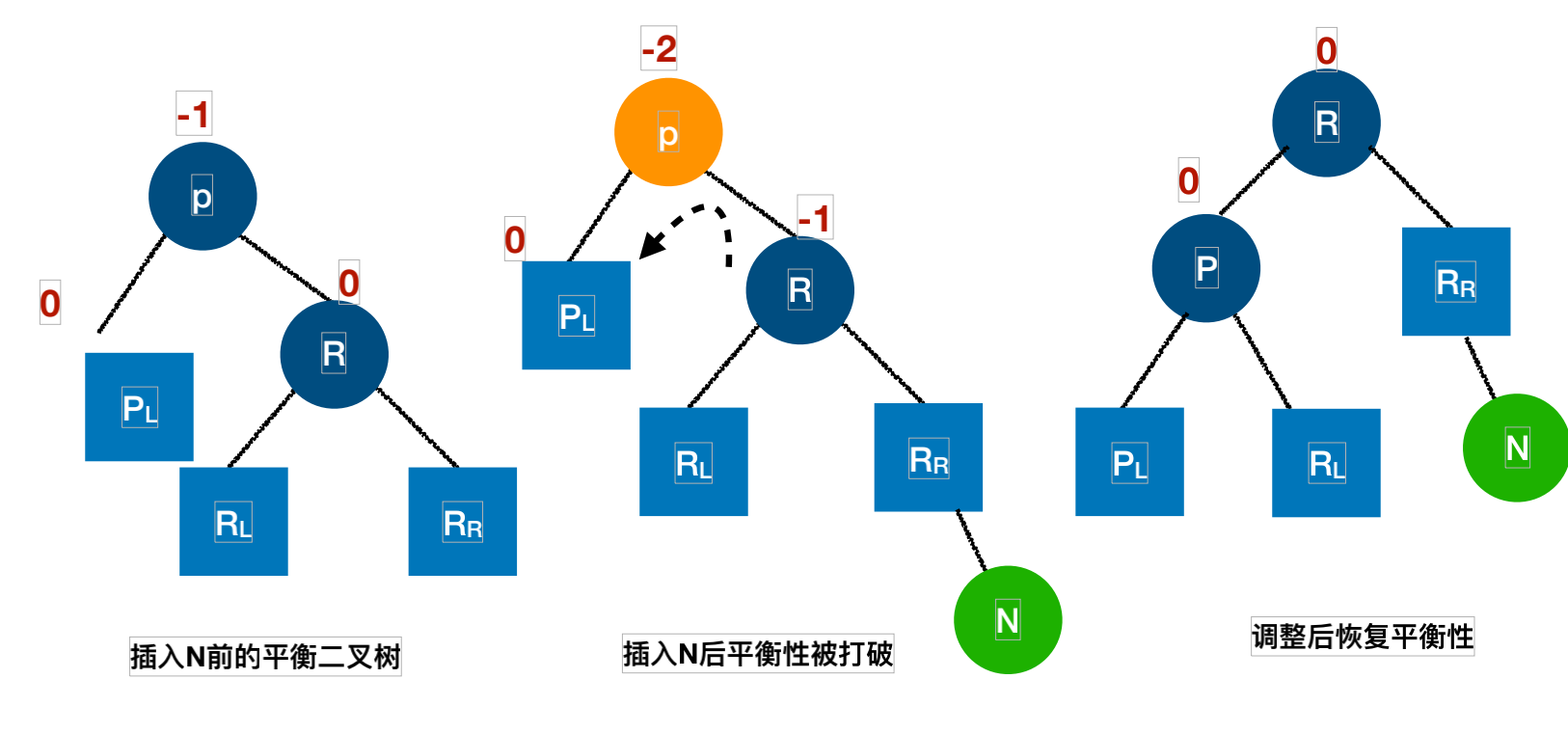
代码实现:
/* 对以P为根的二叉排序树作左旋处理 处理之后P指向新的树根结点,即旋转处理之前的右子树的根结点 */
void L_Rotate(BiTree *p){
BiTree R;
//① R是p的右子树
R = (*p)->rchild;
//② R的左子树作为R的右子树
(*p)->rchild = R->lchild;
//③ 将p作为R的左子树;
R->lchild = (*p);
//④ 将R替换原有p的根结点的位置
*p = R;
}
3个常量:LH左⾼;EH等⾼;RH右⾼;
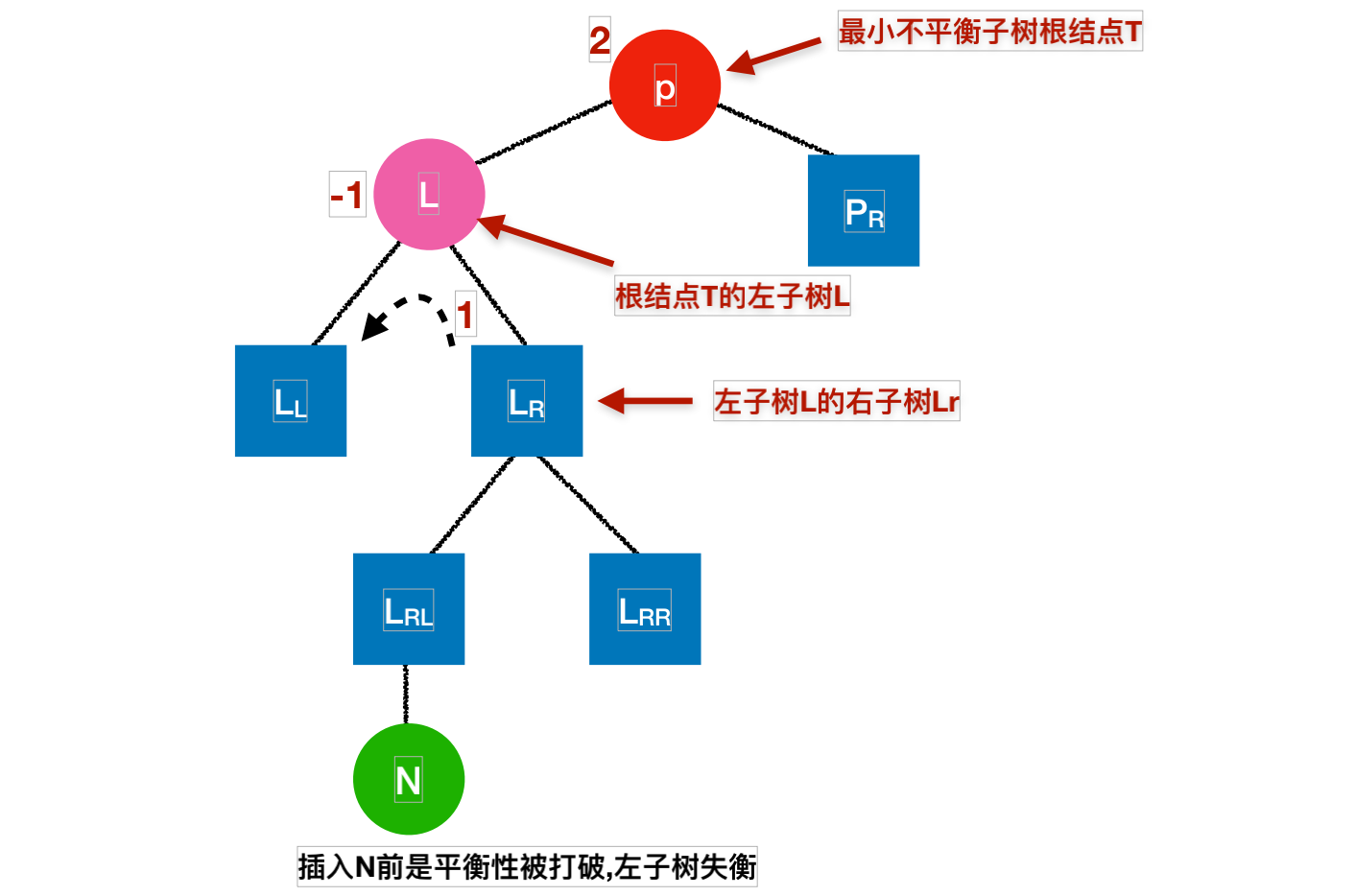
平衡⼆叉树构建模拟(左⼦树失衡的模拟图)

解读:
1.判断T的BF值与L的BF值是否是同符号;
2.将T的BF值与L的BF值更新为平衡后的BF值.等于0;
3.将最⼩不平衡⼦树T进⾏右旋
平衡⼆叉树构建模拟(左⼦树失衡右旋代码实现)
#define LH +1 /* 左高 */#define EH 0 /* 等高 */#define RH -1 /* 右高 */
/*
3. 对指针T所指结点为根的二叉树作左平衡旋转处理,算法结束后,指针T指向平衡处理后新的根结点
*/
void LeftBalance(BiTree *T)
{
BiTree L,Lr;
//1.L指向T的左子树根结点
L=(*T)->lchild;
//2.检查T的左子树的平衡度,并作相应平衡处理
switch(L->bf)
{
//① 新结点插入在T的左孩子的左子树上,要作单右旋处理(如图1-平衡二叉树右旋解释图)
case LH:
//L的平衡因子为LH,即为1时,表示它与根结点BF符合相同,则将它们(T,L)的BF值都改为EH(0)
(*T)->bf=L->bf=EH;
//对最小不平衡子树T进行右旋;
R_Rotate(T);
break;
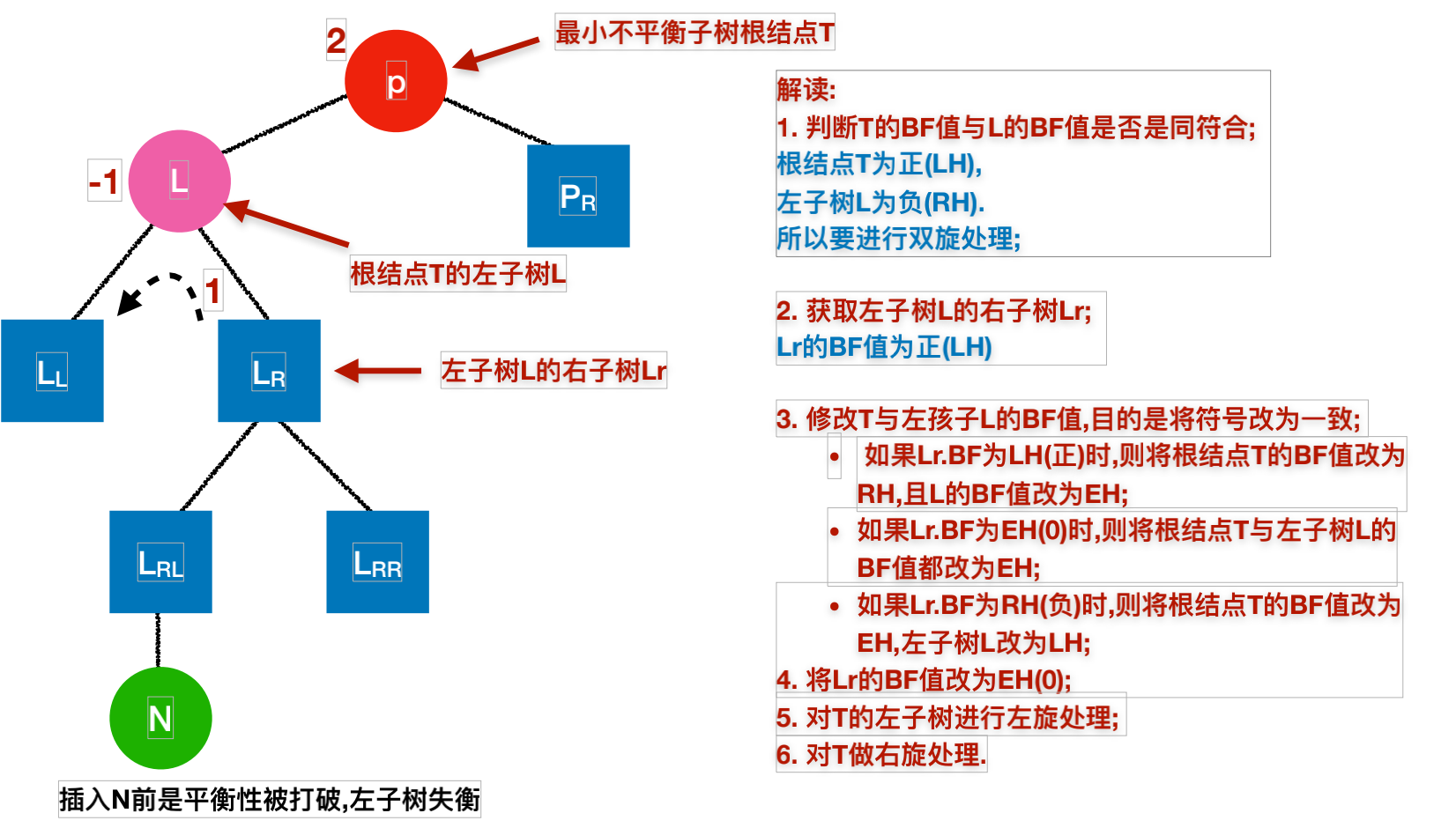
//② LH的平衡因子为RH(-1)时,它与跟结点的BF值符合相反.此时需要做双旋处理(2次旋转处理)
// 新结点插入在T的左孩子的右子树上,要作 双旋处理
case RH:
//Lr指向T的左孩子的右子树根
Lr=L->rchild;
//修改T及其左孩子的平衡因子
switch(Lr->bf)
{
case LH:
(*T)->bf=RH;
L->bf=EH;
break;
case EH:
(*T)->bf=L->bf=EH;
break;
case RH:
(*T)->bf=EH;
L->bf=LH;
break;
}
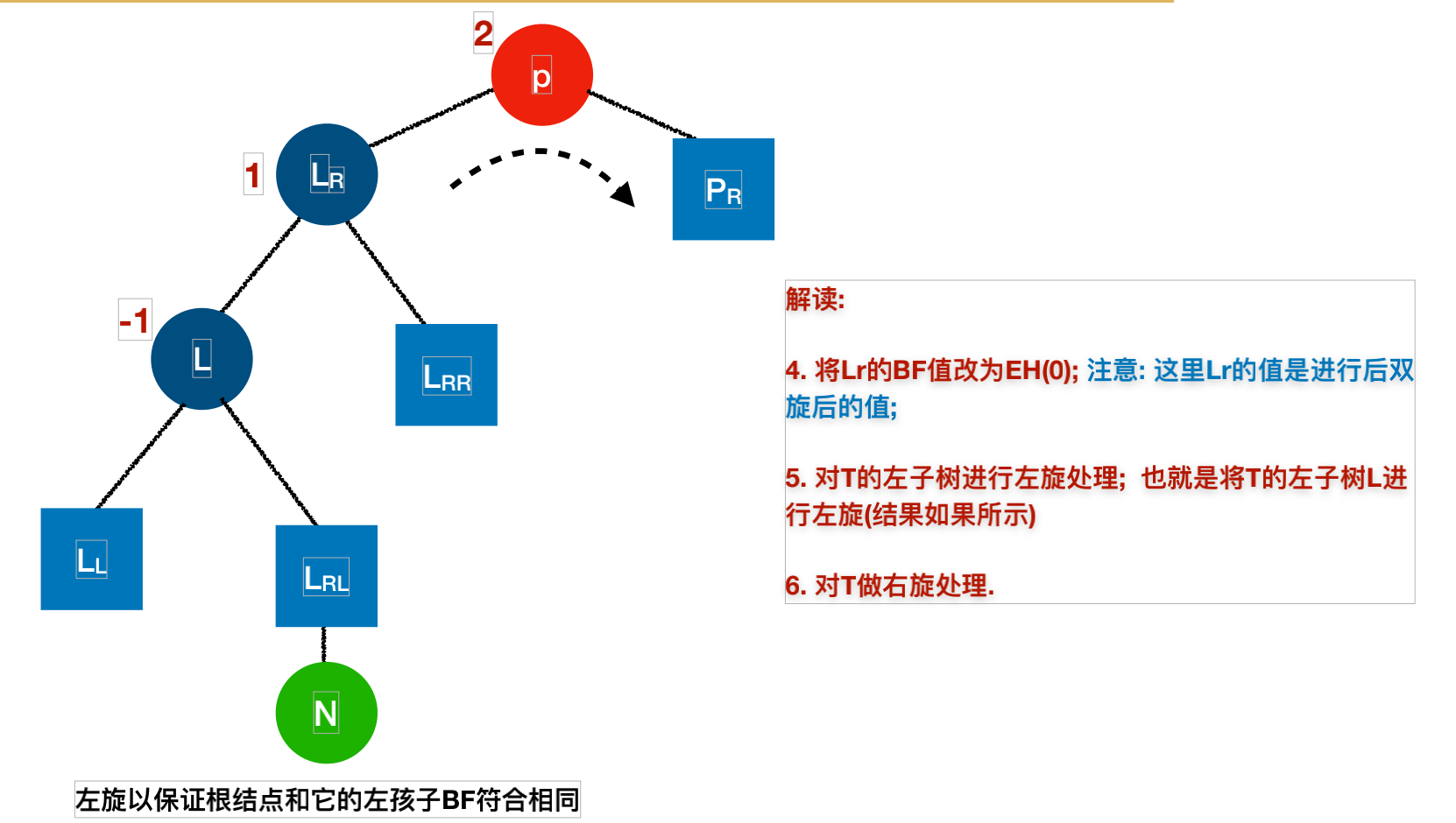
Lr->bf=EH;
//对T的左子树作左旋平衡处理
L_Rotate(&(*T)->lchild);
//对T作右旋平衡处理
R_Rotate(T);
}
}
平衡⼆叉树结点左平衡旋转处理函数实现:
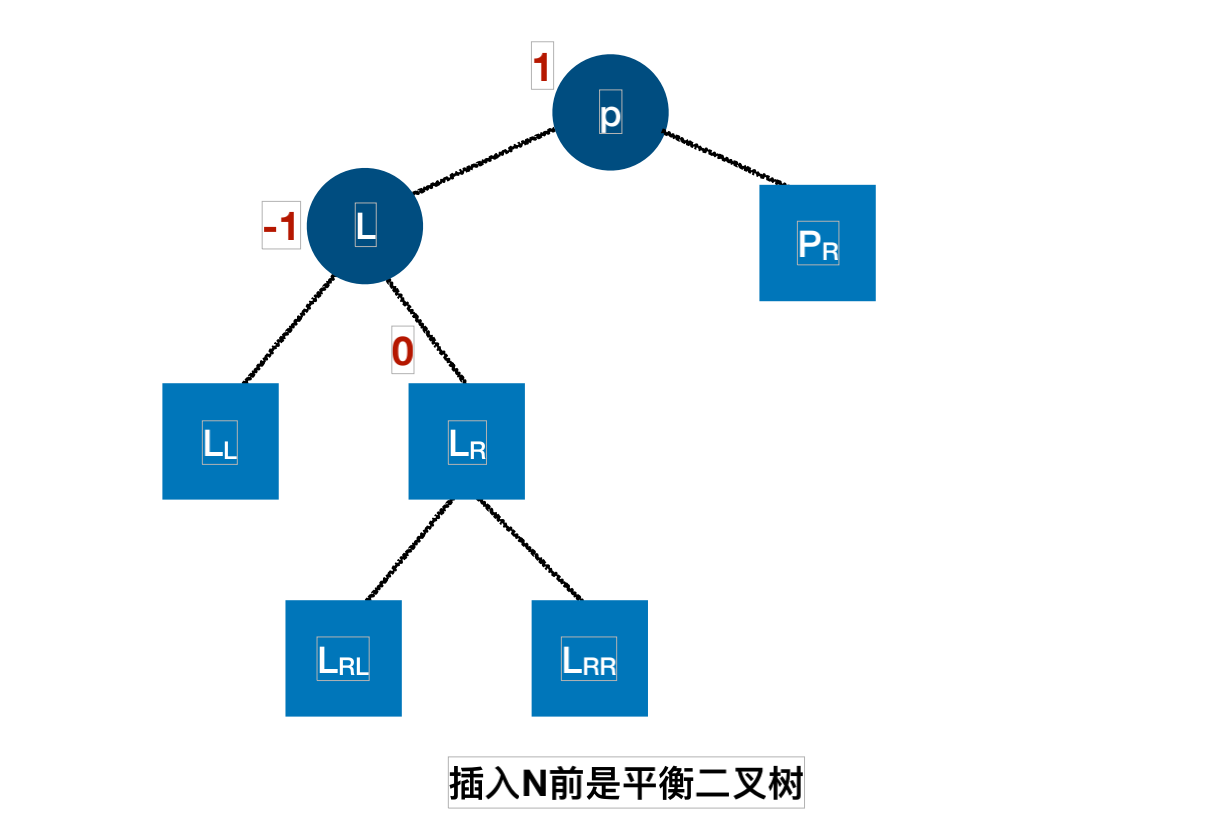
平衡⼆叉树结点左平衡旋转处理函数实现(双旋处理模拟):
平衡⼆叉树构建模拟(右⼦树失衡a双旋代码实现)
/* 对以指针T所指结点为根的二叉树作右平衡旋转处理
本算法结束时,指针T指向新的根结点
*/
void RightBalance(BiTree *T)
{
BiTree R,Rl;
//1.R指向T的右子树根结点
R=(*T)->rchild;
//2. 检查T的右子树的平衡度,并作相应平衡处理
switch(R->bf)
{
//① 新结点插入在T的右孩子的右子树上,要作单左旋处理
case RH:
(*T)->bf=R->bf=EH;
L_Rotate(T);
break;
//新结点插入在T的右孩子的左子树上,要作双旋处理
case LH:
//Rl指向T的右孩子的左子树根
Rl=R->lchild;
//修改T及其右孩子的平衡因子
switch(Rl->bf)
{
case RH:
(*T)->bf=LH;
R->bf=EH;
break;
case EH:
(*T)->bf=R->bf=EH;
break;
case LH:
(*T)->bf=EH;
R->bf=RH;
break;
}
Rl->bf=EH;
//对T的右子树作右旋平衡处理
R_Rotate(&(*T)->rchild);
//对T作左旋平衡处理
L_Rotate(T);
}
}
平衡⼆叉树的插⼊实现
若在平衡的二叉排序树T中不存在和e有相同关键字的结点,则插入一个数据元素为e的新结点,并返回1,否则返回0。若因插入而使二叉排序树失去平衡,则作平衡旋转处理,布尔变量taller反映T长高与否
算法思路:
1.如果T为空时,则创建一个新结点;
2.如果T不为空,判断是否存在相同的结点.如果二叉树中存在相同结点,则不需要插入;
3.如果新结点值e小于T的根结点值,则在T的左子树查找;
-如果能在左子树中查找到,则不插入进去.返回False; 如果没有找到,则插入
-插入成功taller为TRUE,说明新结点e已经插入进去; 此时需要判断T的平衡因子;
-如果平衡因子是1,则说明左子树高于右子树,那么需要调用leftBalance进行左平衡旋转处理;
-如果为0或者-1,则说明新插入的结点没有让整颗二叉排序树失去平衡性,只需要修改BF值即可;
4.如果新结点值e大于T的根结点值,则在T的右子树查找;
-如果能在右子树中查找到,则不插入进去.返回False; 如果没有找到,则插入
-插入成功taller为TRUE,说明新结点e已经插入进去; 此时需要判断T的平衡因子;
-如果平衡因子是-1,则说明右子树高于左子树,那么需要调用RightBalance进行右平衡旋转处理;
-如果为0或者1,则说明新插入的结点没有让整颗二叉排序树失去平衡性,只需要修改BF值即可;
Status InsertAVL(BiTree *T,int e,Status *taller)
{
if(!*T)
{ //1.插入新结点,树“长高”,置taller为TRUE
//① 开辟一个新结点T;
*T=(BiTree)malloc(sizeof(BiTNode));
//② 对新结点T的data赋值,并且让其左右孩子指向为空,T的BF值为EH;
(*T)->data=e;
(*T)->lchild=(*T)->rchild=NULL;
(*T)->bf=EH;
//③ 新结点默认"长高"
*taller=TRUE;
}
else
{
if (e==(*T)->data)
{ //2.树中已存在和e有相同关键字的结点则不再插入
*taller=FALSE;
return FALSE;
}
if (e<(*T)->data)
{
//3.应继续在T的左子树中进行搜索
if(!InsertAVL(&(*T)->lchild,e,taller))
//未插入
return FALSE;
//4.已插入到T的左子树中且左子树“长高”
if(*taller)
//5.检查T的平衡度
switch((*T)->bf)
{
case LH:
//原本左子树比右子树高,需要作左平衡处理
LeftBalance(T);
*taller=FALSE;
break;
case EH:
//原本左、右子树等高,现因左子树增高而使树增高
(*T)->bf=LH;
*taller=TRUE;
break;
case RH:
//原本右子树比左子树高,现左、右子树等高
(*T)->bf=EH;
*taller=FALSE;
break;
}
}
else
{ //6.应继续在T的右子树中进行搜索
//未插入
if(!InsertAVL(&(*T)->rchild,e,taller))
return FALSE;
//已插入到T的右子树且右子树“长高”
if(*taller)
// 检查T的平衡度
switch((*T)->bf)
{
//原本左子树比右子树高,现左、右子树等高
case LH:
(*T)->bf=EH;
*taller=FALSE;
break;
//原本左、右子树等高,现因右子树增高而使树增高
case EH:
(*T)->bf=RH;
*taller=TRUE;
break;
// 原本右子树比左子树高,需要作右平衡处理
case RH:
RightBalance(T);
*taller=FALSE;
break;
}
}
}
return TRUE;
}
二叉排序树查找
Status SearchBST(BiTree T,int key,BiTree f, BiTree *p){
if (!T) /* 查找不成功 */
{
*p = f;
return FALSE;
}
else if (key==T->data) /* 查找成功 */
{
*p = T;
return TRUE;
}
else if (key<T->data)
return SearchBST(T->lchild, key, T, p); /* 在左子树中继续查找 */
else
return SearchBST(T->rchild, key, T, p); /* 在右子树中继续查找 */
}
main函数执行打印:
int main(int argc, const char * argv[]) {
printf("平衡二叉树 !\n");
int i;
int a[10]={3,2,1,4,5,6,7,10,9,8};
//调整数组的顺序,最终生成的平衡二叉树高度是一样的.
//int a[10]={8,9,1,4,5,6,7,10,2,3};
//int a[10]={9,4,1,2,7,6,5,10,3,8};
BiTree T=NULL;
Status taller;
int sum = 0;
for(i=0;i<10;i++)
{
InsertAVL(&T,a[i],&taller);
sum += taller;
printf("插入%d,是否增加树的高度(%d)[YES->1 / NO->0]\n",a[i],taller);
}
printf("将数组a插入到平衡二叉树后,最终形成高度为%d的平衡二叉树\n",sum);
BiTree p;
int statusValue = SearchBST(T, 10, NULL, &p);
printf("查找%d是否成功:%d (1->YES/0->NO)\n",p->data,statusValue);
return 0;
}
打印结果:

散列查找(哈希表)技术
散列技术是记录的存储位置和它的关键字之间建⽴⼀个确定的对应关系f,使得每个关键字key对应⼀个存储位置f(key).查找时,根据这个对应关系找到给定值
key的映射f(key).若查找集合中存在这个记录,则必定在f(key)的位置上.
- 直接地址法
f(key)=a*key+b(a,b为常数);
适合于简单、均匀、不容易冲突,关键子分布,查找表少连序
- 数字分析法

PS:前面3位叫接入号,中间4位位运营商的子品牌,最后4位位归属地
- 平⽅取中法
如:12342=1522756,取中间部分叫平方取中法,适合那种数据不是连贯的数字
- 折叠法
折叠法就是将关键字从左到右分割成位数相等的⼏部分(注意最后⼀部分位数不够可以稍微短些);然后将⼏部分叠加求和,并按散列表表⻓,取后⼏位作为散列地址.
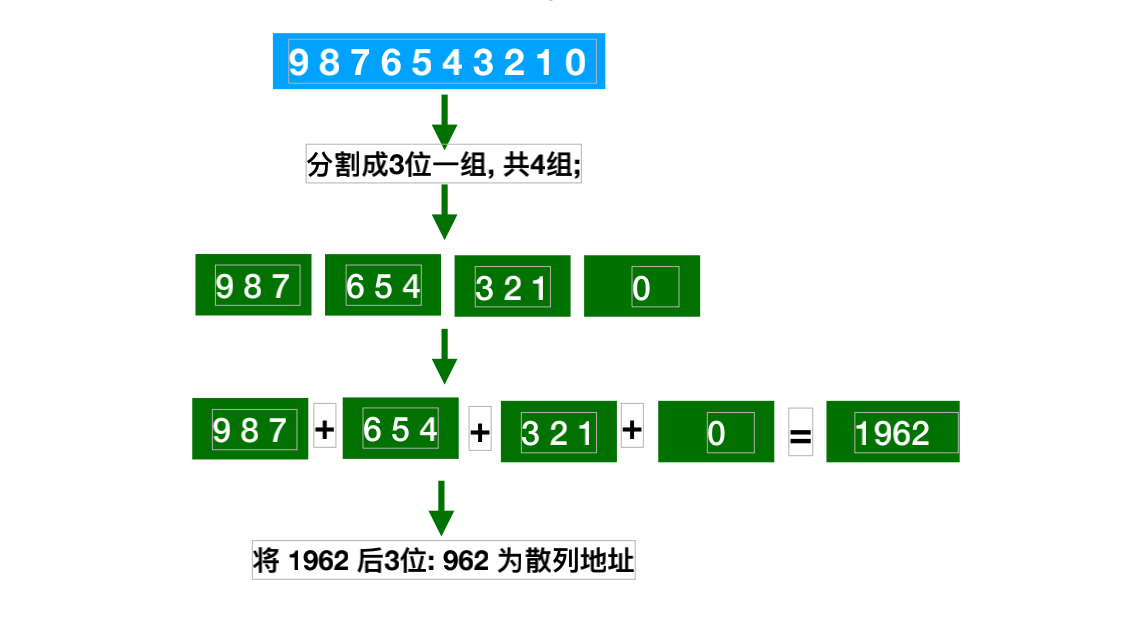
- 除留余数法
f(key)=keymodp(p<=m)
- 除留余数法
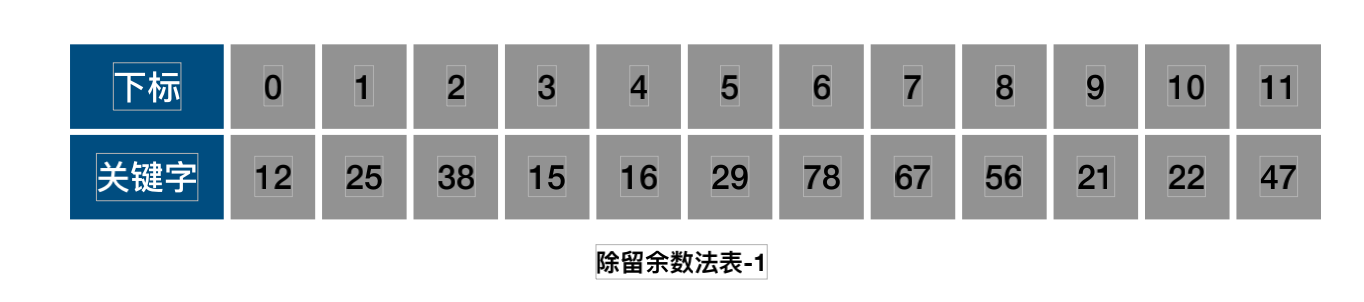
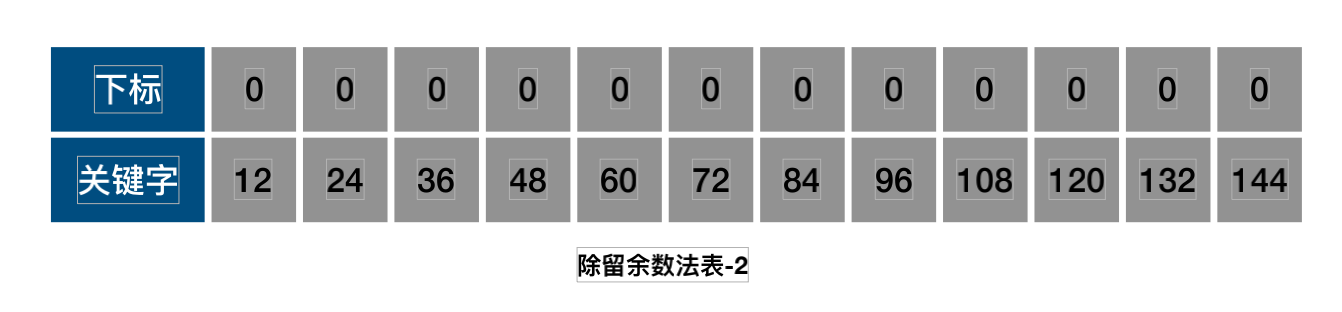
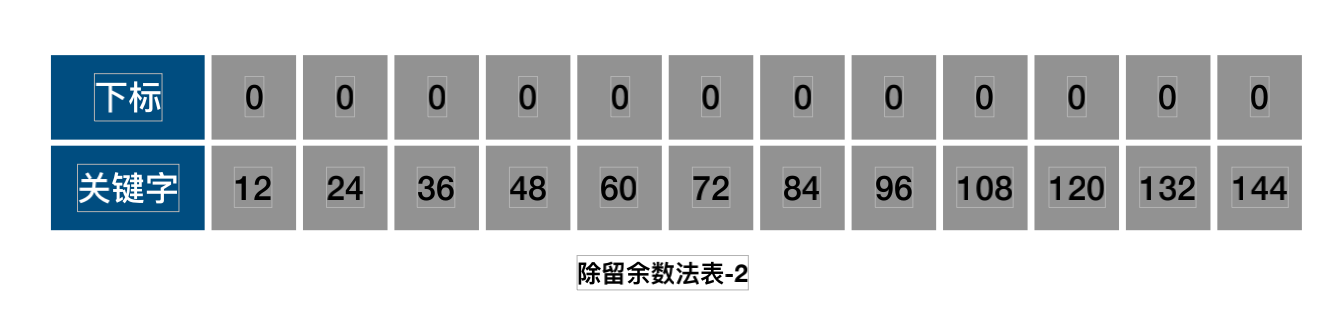
- 随机数法
f(key)=random(key);
开放定址法
开放定址法就是⼀旦发⽣了冲突,就去寻找下⼀个空的散列地址.只有散列表⾜够⼤,空的散列地址总能找到,并将记录存⼊.
开放定址法公式:
fi(key)=(f(key)+di)Modm;(di=1,2,3,……,m-1)
关键字集合{12,67,56,16,25,37,22,29,15,47,48,34}表⻓为12,我们⽤散列函数f(key)=key mod12;
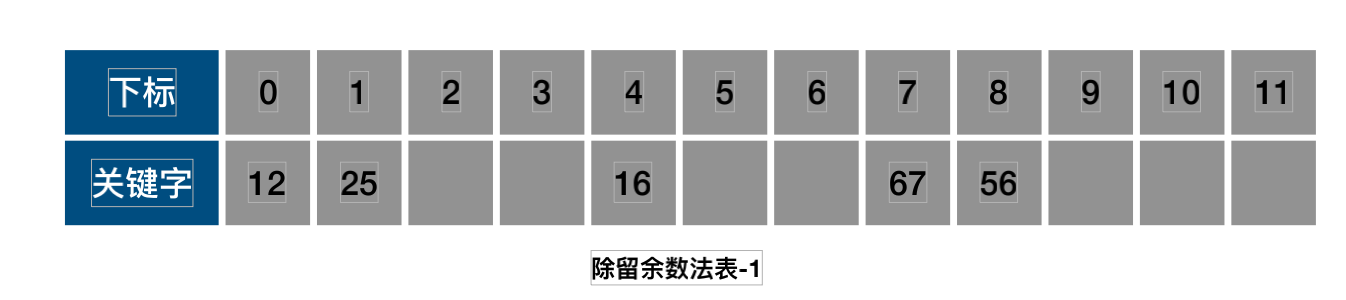
1.key=37时,f(37)=1,与25发⽣冲突;
2.使⽤开放定址公式:f(37)=(f(37)+1)mod12=2.3.发现下标为2位置上是空.即可存储下来.
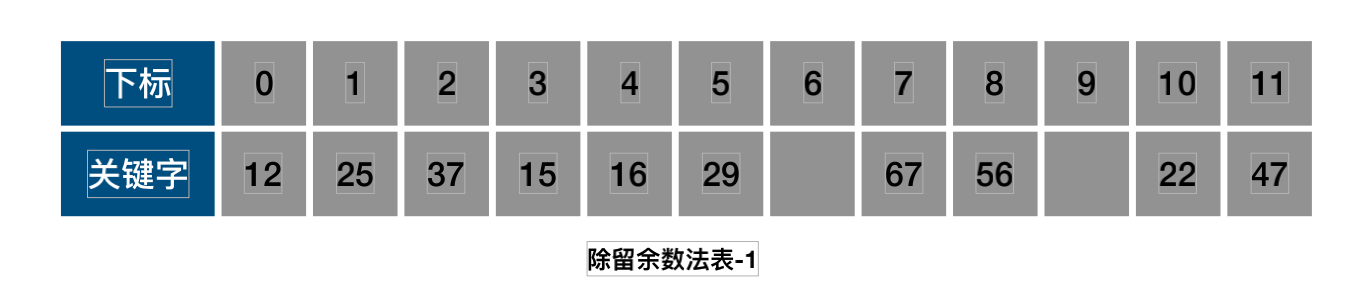
1.存储22,2915,47按照f(key)=keymod12,没有出现冲突,即可直接存储进去.
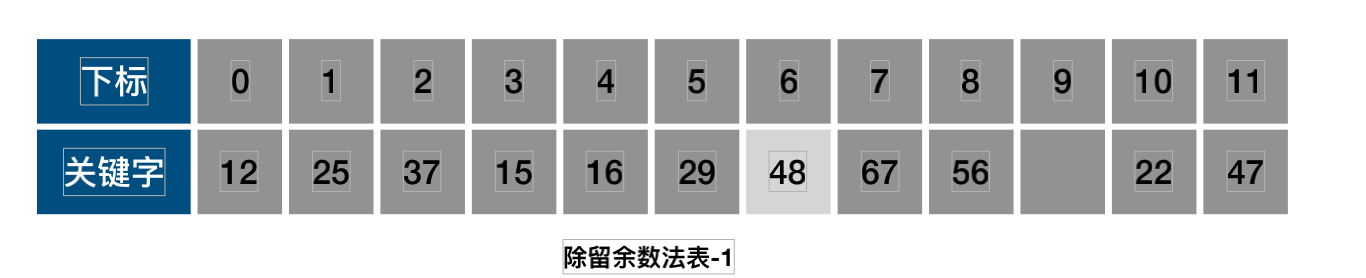
- f(48)=48mod12=0;此时0这个位置上已经存储了数据12.那么12和48就是同义词了.
- 使⽤开放定址法公式f(48)=(f(48)+2)mod12=1;于是又和25发⽣冲突了.
- 继续往下,使⽤开放定址法公式.直到f(48)=(f(48)+6)mod12=6时.此时6的位置上没有数据,则将48存储到下标为6的位置上;
开放定址法就是⼀旦发⽣了冲突,就去寻找下⼀个空的散列地址.只有散列表⾜够⼤,空的散列地址总能找到,并将记录存⼊.
开放定址法公式:
fi(key)=(f(key)+di)Modm;(di=1,2,3,……,m-1)
总结:解决冲突的开放定址法称为线性探测法
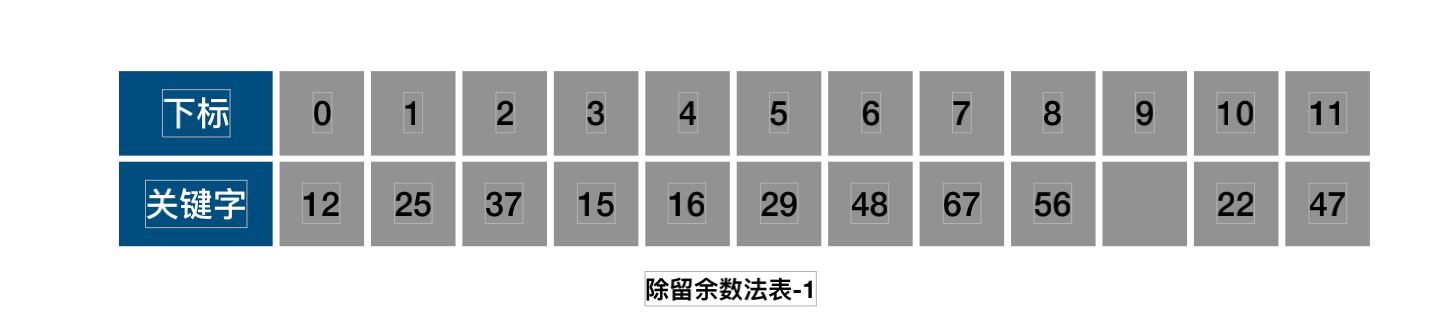
- f(34)=10.但是10的位置是22.34和22发⽣了冲突~
- 但是此时10以后的位置已经没有空间来存储了.但是10的前⾯是有空间的;
- .通过开放定址公式,⼀直取模求余,最终能得到结果.存储34.
- 但是这样的计算效率⾮常低下
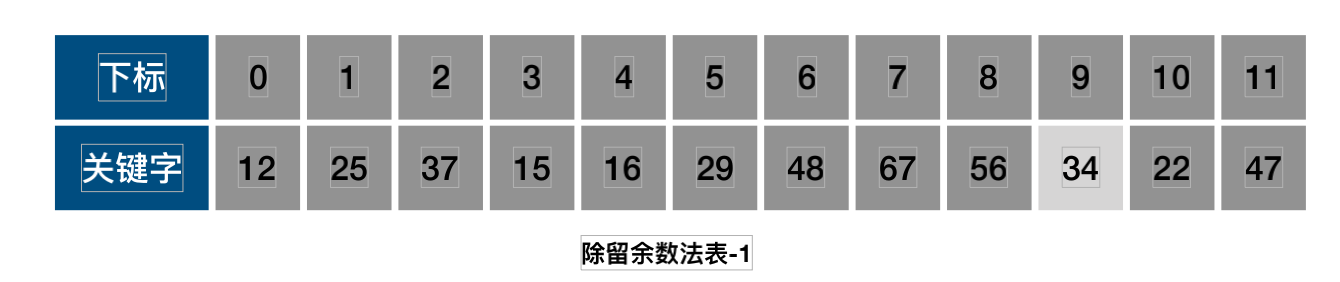
- 1.di={12,-12,22,-22,…,q2,-q2,q<=m/2}
- f(34)=(f(34)+1)mod12=11;下标11上已经存储了47.继续计算
- f(34)=(f(34)-1)mod12=9;9的位置上为空,可以存储34
开放定址法就是⼀旦发⽣了冲突,就去寻找下⼀个空的散列地址.只有散列表⾜够⼤,空的散列地址总能找到,并将记录存⼊.
开放定址法公式:
fi(key)=(f(key)+di)Modm; di={12,-12,22,-22,…,q2,-q2,q<=m/2}
再散列函数法
对于散列表来说,我们事先准备多个散列函数:
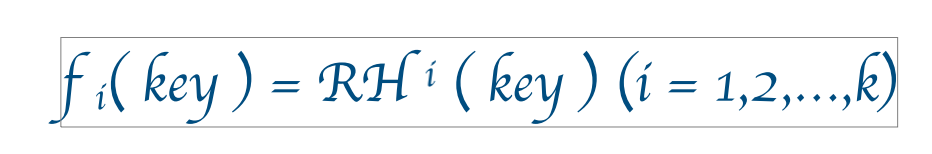
RHi指的是不同的散列函数.
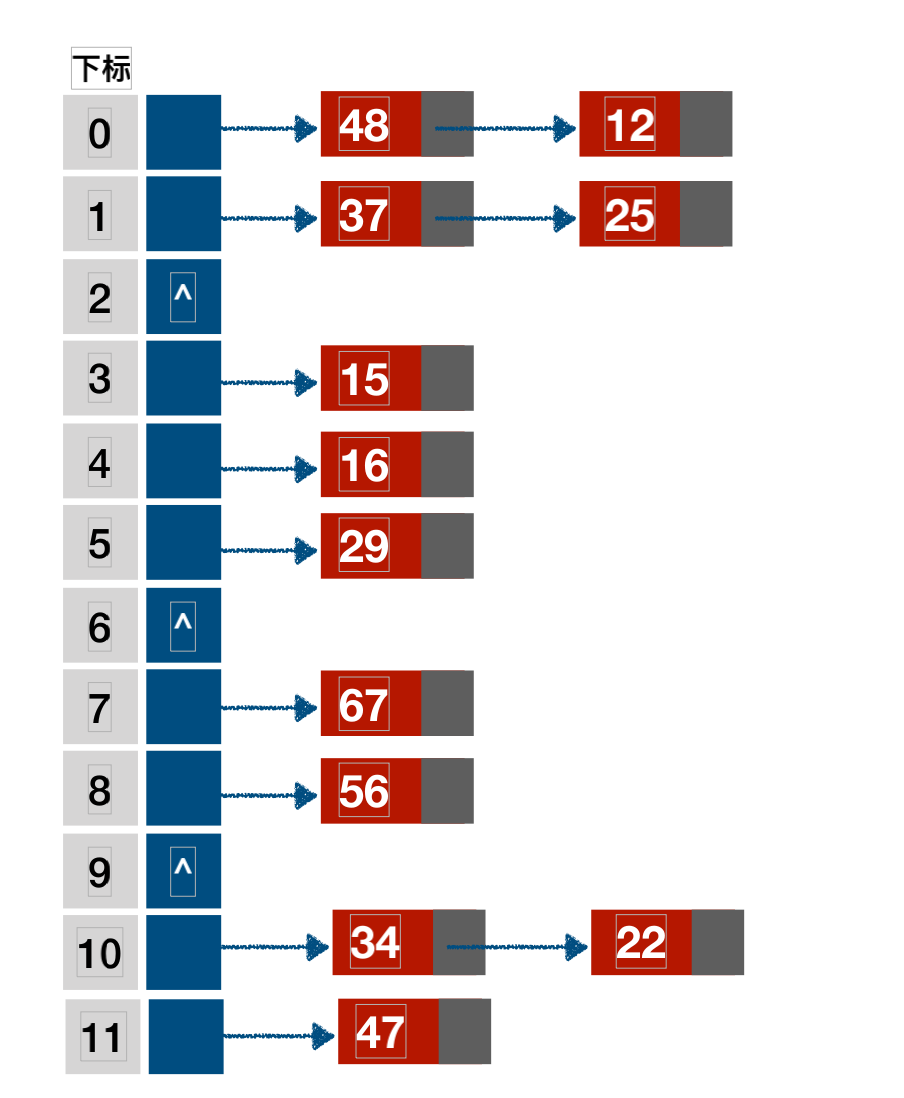
链地址法
将所有的关键字为同义词的记录存储在⼀个单链表中,我们称为这种同义词⼦表.在散列表中只存储所有同义词⼦表的头指针(头地址).
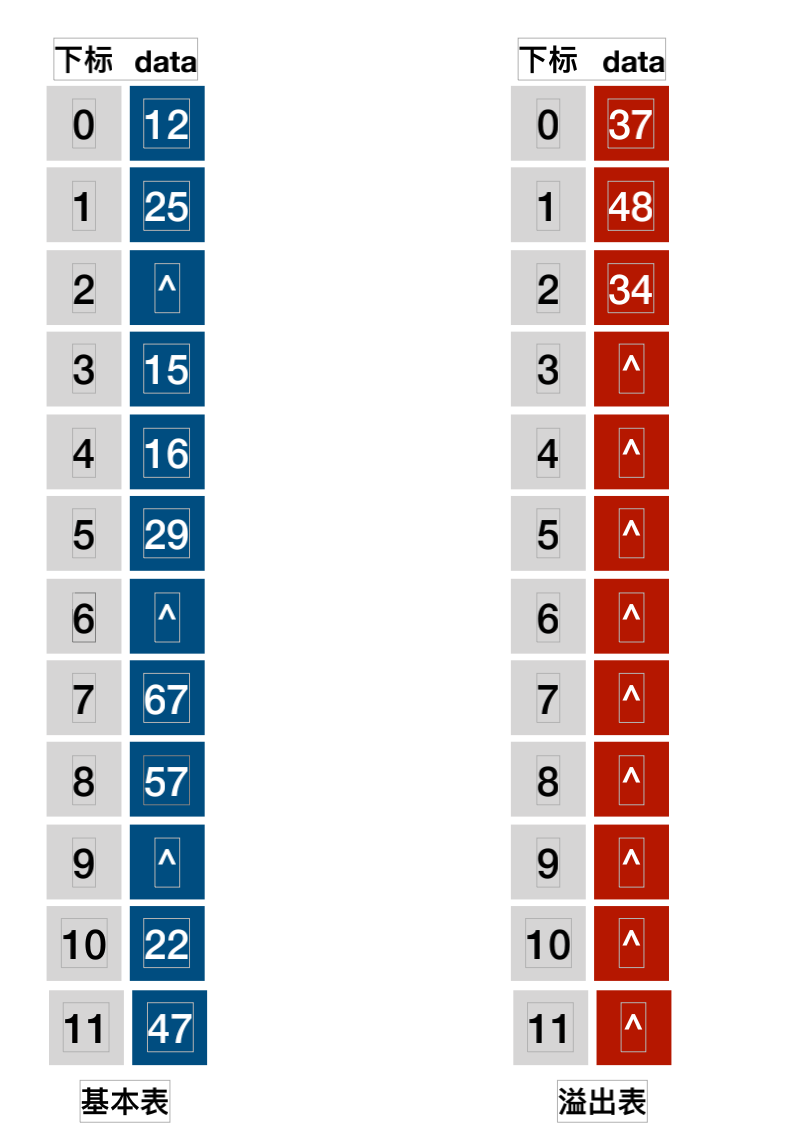
散列表查找实现
- 散列表结构设计
typedef struct
{
//数据元素存储基址,动态分配数组
int *elem;
//当前数据元素个数
int count;
}HashTable;
int m=0; /* 散列表表长,全局变量 */
- 初始化散列表
- .设计散列函数
- 插⼊关键字到散列表
- 在散列表中插⼊关键字
主要代码实现
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
typedef int Status;
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100 //存储空间初始分配量
#define SUCCESS 1
#define UNSUCCESS 0
//定义散列表长为数组的长度
#define HASHSIZE 12
#define NULLKEY -32768
typedef struct
{
//数据元素存储基址,动态分配数组
int *elem;
//当前数据元素个数
int count;
}HashTable;
int m=0; /* 散列表表长,全局变量 */
//1.初始化散列表
Status InitHashTable(HashTable *H)
{
int i;
//① 设置H.count初始值; 并且开辟m个空间
m=HASHSIZE;
H->count=m;
H->elem=(int *)malloc(m*sizeof(int));
//② 为H.elem[i] 动态数组中的数据置空(-32768)
for(i=0;i<m;i++)
H->elem[i]=NULLKEY;
return OK;
}
//2. 散列函数
int Hash(int key)
{
//除留余数法
return key % m;
}
//3. 插入关键字进散列表
void InsertHash(HashTable *H,int key)
{
//① 求散列地址
int addr = Hash(key);
//② 如果不为空,则冲突
while (H->elem[addr] != NULLKEY)
{
//开放定址法的线性探测
addr = (addr+1) % m;
}
//③ 直到有空位后插入关键字
H->elem[addr] = key;
}
//4. 散列表查找关键字
Status SearchHash(HashTable H,int key,int *addr)
{
//① 求散列地址
*addr = Hash(key);
//② 如果不为空,则冲突
while(H.elem[*addr] != key)
{
//③ 开放定址法的线性探测
*addr = (*addr+1) % m;
//④H.elem[*addr] 等于初始值或者循环有回到了原点.则表示关键字不存在;
if (H.elem[*addr] == NULLKEY || *addr == Hash(key))
//则说明关键字不存在
return UNSUCCESS;
}
return SUCCESS;
}
int main(int argc, const char * argv[]) {
// insert code here...
printf("Hello, World!\n");
int arr[HASHSIZE]={12,67,56,16,25,37,22,29,15,47,48,34};
int i,p,key,result;
HashTable H;
//1.初始化散列表
InitHashTable(&H);
//2.向散列表中插入数据
for(i=0;i<m;i++)
InsertHash(&H,arr[i]);
//3.在散列表查找key=39
key=39;
result=SearchHash(H,key,&p);
if (result)
printf("查找 %d 的地址为:%d \n",key,p);
else
printf("查找 %d 失败。\n",key);
//4.将数组中的key,打印出所有在散列表的存储地址
for(i=0;i<m;i++)
{
key=arr[i];
SearchHash(H,key,&p);
printf("查找 %d 的地址为:%d \n",key,p);
}
return 0;
}
打印结果: