一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

图是连通图;
图中包含了了N个顶点;
图中边的数量等于N-1条边.

假设有如下图

先直接给出其最小生成树如下

如何生成？往下看

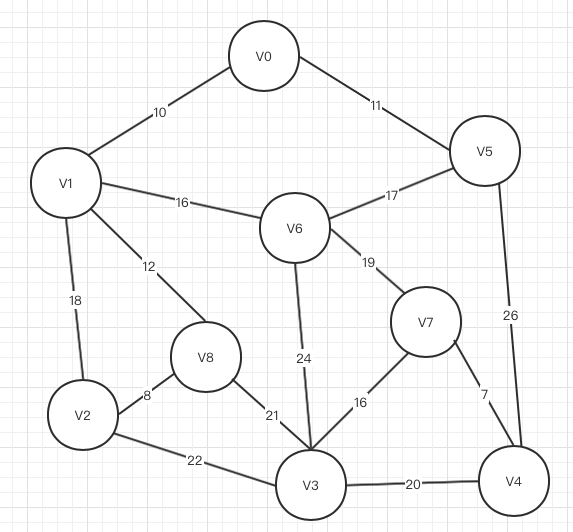
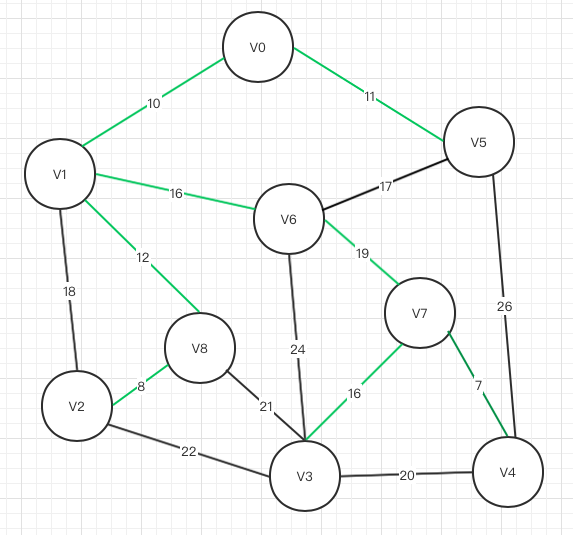
Prim算法

输入：一个加权连通图，其中顶点集合为V，边集合为E；
初始化：Vnew = {x}，其中x为集合V中的任一节点（起始点），Enew = {},为空；
重复下列操作，直到Vnew = V： a.在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）； b.将v加入集合Vnew中，将<u, v>边加入集合Enew中；
输出：使用集合Vnew和Enew来描述所得到的最小生成树。

简单的说，从所有可选结点 （所有可以联通到已选结点并且未被选择的结点） 中再选择权重最小的结点，并将其加入已选节点；重复操作，直到所有节点被选择完毕，全部节点走通。

不懂？没事，跟着下面来一遍以上图为例

注意⚠️：绿色代表已联通，红色代表下一轮的可选边和结点，黑色线表示不可联通或暂未联通

第一轮从V0开始

可选节点为V1 V5，从可选结点中选择权重最小的，所以V0->V1,V1被选择

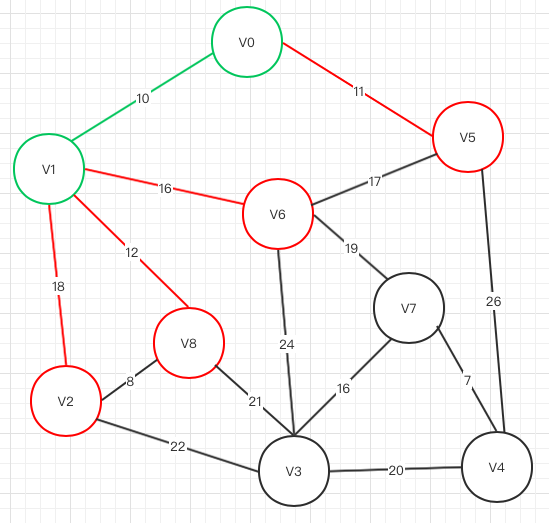
第二轮

上一轮中，V0 V1已选，所以接下来能够联通到V0 V1的均为可选结点，可选节点：V2 V8 V6 V5；权重最小的是V0->V5,所以V5被选择，剩下红色待选

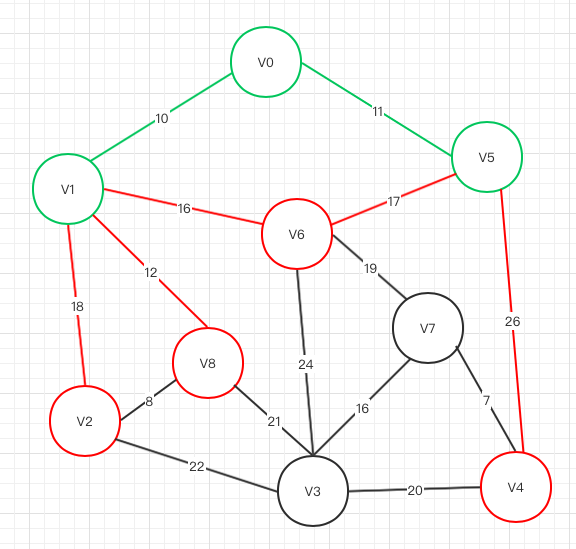
第三轮

上图可选节点：V2 V8 V6 V4, 其中V1->V8权重最小，V8被选择，剩下红色待选

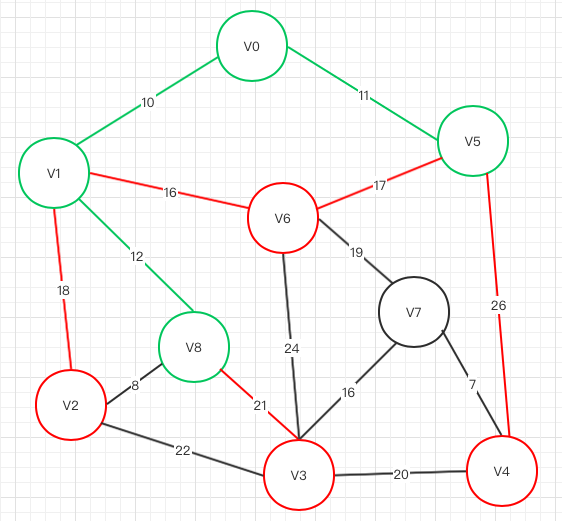
第四轮

上图可选结点为：V2 V3 V6 V4, V8->V2 权重最小，V2被选择，剩下红色待选

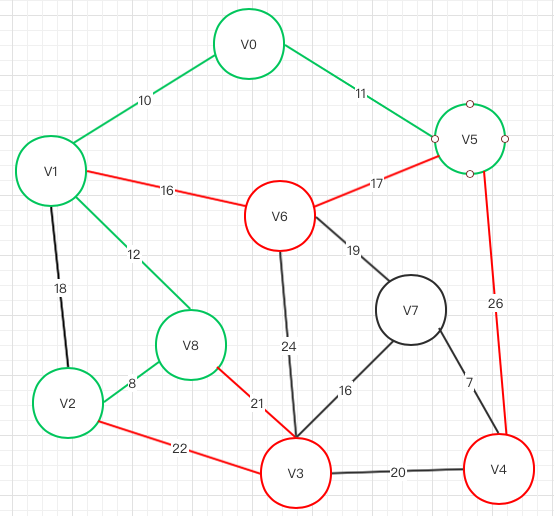
第五轮

上图可选节点：V3 V6 V4 ，其中V1->V6权重最小，V6被选择，剩下红色待选

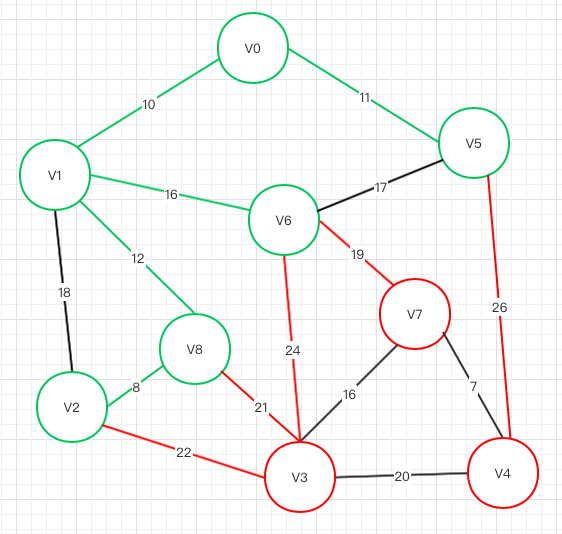
第六轮

上图可选节点：V3 V7 V4，其中V6->V7权重最小，V7被选择，剩下红色待选

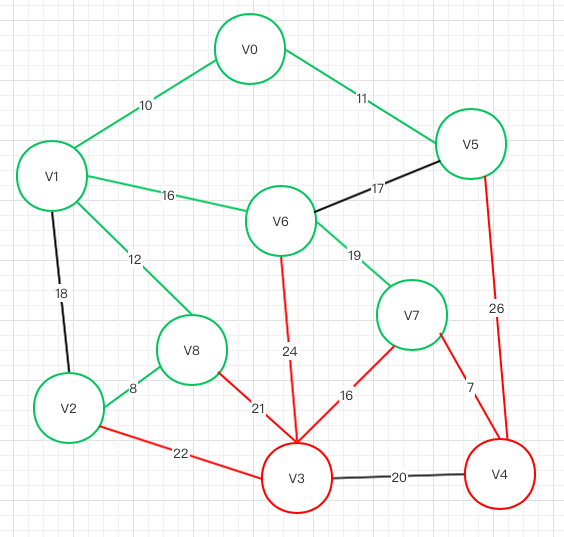
第七轮

上图只剩V3 和 V4 V7->V4权重最小，所以V4被选择，还剩V3

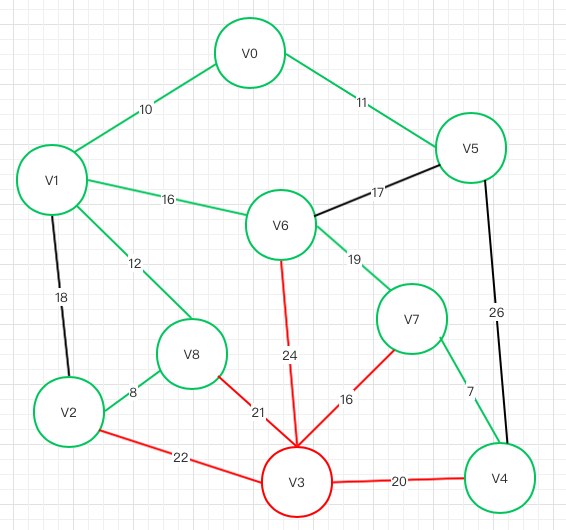
第八轮

V2 V8 V6 V7 V4 都可以连接到V3，只有V7->V3权重最小，所以最终结果如下

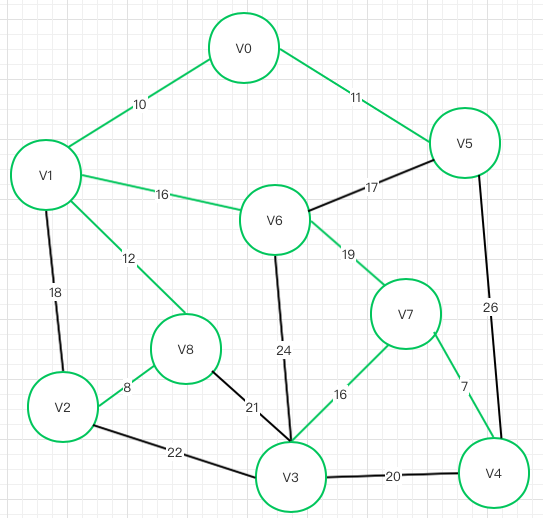
代码实现思路

定义2个数组; adjvex ⽤用来保存相关顶点下标; lowcost 保存顶点之间的权值
初始化2个数组, 从v0开始寻找最小生成树, 默认v0是最⼩生成树上第一个顶点 3. 循环lowcost 数组,根据权值,找到顶点 k;
更新lowcost 数组
循环所有顶点,找到与顶点k 有关系的顶点. 并更更新lowcost 数组与adjvex 数组; 注意: 更新lowcost 数组与adjvex 数组的条件:
与顶点k 之间有连接
当前结点 j 没有加入过最⼩小⽣生成树;
顶点 k 与当前顶点 j 之间的权值小于顶点j 与其他顶点 k 之前的权值. 则更新. 简单说就是要⽐较之前存储的值要小,则更新;

定义

#include "stdio.h"
#include "stdlib.h"

#include "math.h"
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAXEDGE 20
#define MAXVEX 20
#define INFINITYC 65535

typedef int Status;    /* Status是函数的类型,其值是函数结果状态代码，如OK等 */

typedef struct
{
    int arc[MAXVEX][MAXVEX];
    int numVertexes, numEdges;
}MGraph;

核心函数

void MiniSpanTree_Prim(MGraph G)
{
    int min, i, j, k;
    int sum = 0;
    /* 保存相关顶点下标 */
    int adjvex[MAXVEX];
    /* 保存相关顶点间边的权值 */
    int lowcost[MAXVEX];
    
    /* 初始化第一个权值为0，即v0加入生成树 */
    /* lowcost的值为0，在这里就是此下标的顶点已经加入生成树 */
    lowcost[0] = 0;
    
    /* 初始化第一个顶点下标为0 */
    adjvex[0] = 0;
    
    //1. 初始化
    for(i = 1; i < G.numVertexes; i++)    /* 循环除下标为0外的全部顶点 */
    {
        lowcost[i] = G.arc[0][i];    /* 将v0顶点与之有边的权值存入数组 */
        adjvex[i] = 0;                    /* 初始化都为v0的下标 */
    }
    
    //2. 循环除了下标为0以外的全部顶点, 找到lowcost数组中最小的顶点k
    for(i = 1; i < G.numVertexes; i++)
    {
        /* 初始化最小权值为∞， */
        /* 通常设置为不可能的大数字如32767、65535等 */
        min = INFINITYC;
        
        j = 1;k = 0;
        while(j < G.numVertexes)    /* 循环全部顶点 */
        {
            /* 如果权值不为0且权值小于min */
            if(lowcost[j]!=0 && lowcost[j] < min)
            {
                /* 则让当前权值成为最小值,更新min */
                min = lowcost[j];
                /* 将当前最小值的下标存入k */
                k = j;
            }
            j++;
        }
        
        /* 打印当前顶点边中权值最小的边 */
        printf("(V%d, V%d)=%d\n", adjvex[k], k ,G.arc[adjvex[k]][k]);
        sum+=G.arc[adjvex[k]][k];
        
        /* 3.将当前顶点的权值设置为0,表示此顶点已经完成任务 */
        lowcost[k] = 0;
        
        /* 循环所有顶点,找到与顶点k 相连接的顶点
         1. 与顶点k 之间连接;
         2. 该结点没有被加入到生成树;
         3. 顶点k 与 顶点j 之间的权值 < 顶点j 与其他顶点的权值,则更新lowcost 数组;
         
         */
        for(j = 1; j < G.numVertexes; j++)
        {
            /* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */
            if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j])
            {
                /* 将较小的权值存入lowcost相应位置 */
                lowcost[j] = G.arc[k][j];
                /* 将下标为k的顶点存入adjvex */
                adjvex[j] = k;
            }
        }
    }
    printf("sum = %d\n",sum);
}

创建测试用例

void CreateMGraph(MGraph *G)/* 构件图 */
{
    int i, j;
    
    /* printf("请输入边数和顶点数:"); */
    G->numEdges=15;
    G->numVertexes=9;
    
    for (i = 0; i < G->numVertexes; i++)/* 初始化图 */
    {
        for ( j = 0; j < G->numVertexes; j++)
        {
            if (i==j)
                G->arc[i][j]=0;
            else
                G->arc[i][j] = G->arc[j][i] = INFINITYC;
        }
    }
    
    G->arc[0][1]=10;
    G->arc[0][5]=11;
    G->arc[1][2]=18;
    G->arc[1][8]=12;
    G->arc[1][6]=16;
    G->arc[2][8]=8;
    G->arc[2][3]=22;
    G->arc[3][8]=21;
    G->arc[3][6]=24;
    G->arc[3][7]=16;
    G->arc[3][4]=20;
    G->arc[4][7]=7;
    G->arc[4][5]=26;
    G->arc[5][6]=17;
    G->arc[6][7]=19;
    
    for(i = 0; i < G->numVertexes; i++)
    {
        for(j = i; j < G->numVertexes; j++)
        {
            G->arc[j][i] =G->arc[i][j];
        }
    }
    
}

kruskal算法

还是这个图

算法思路

将邻接矩阵转化成边表数组;
对边表数组根据权值按照从小到大的顺序排序;
遍历所有的边, 通过parent 数组找到边的连接信息; 避免闭环问题;
如果不存在闭环问题,则加入到最⼩⽣成树中. 并且修改parent 数组

注意⚠️ parent 数组的目的是为了判断当前的边是否会构成闭环

1、将邻接矩阵转化成边表数组，对边表数组根据权值按照从⼩小到⼤大的顺序排序;

规定小下标到大下标的方向

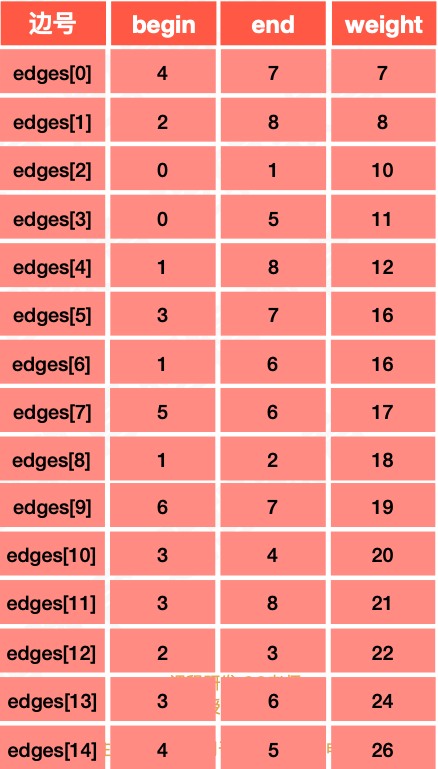
2、开始生成：条件是思路中的3和4

按照上面的排序，V4->V7

不存在闭环，所以可以联通

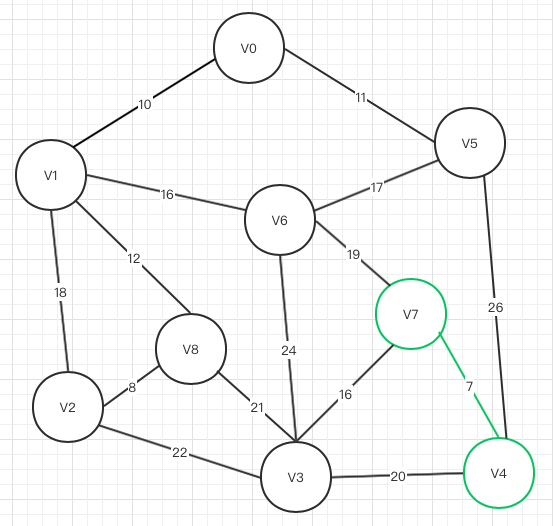
V2->V8

不存在闭环，可以联通

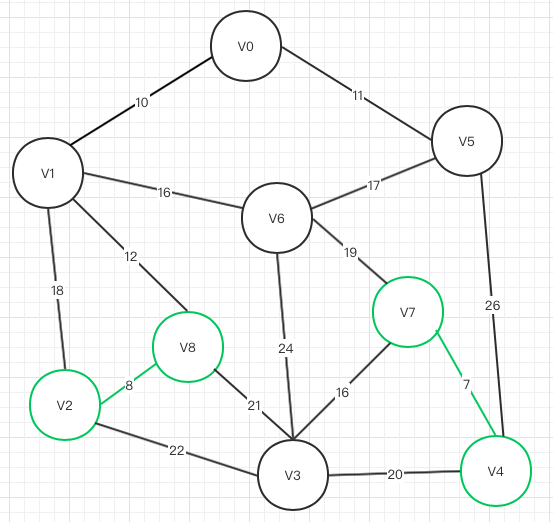
V0->V1

不存在闭环，可以联通

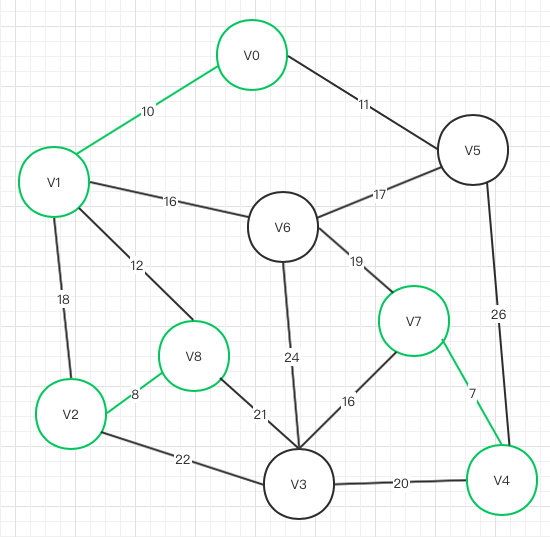
V0->V5

不存在闭环，可以联通

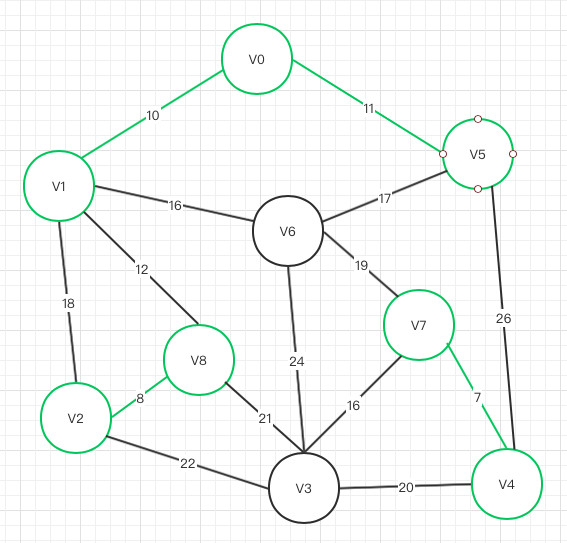
V1->V8

不存在闭环，可以联通

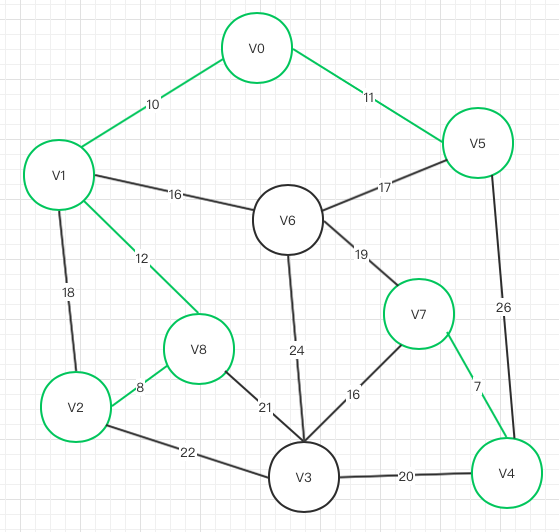
V3->V7

不存在闭环，可以联通

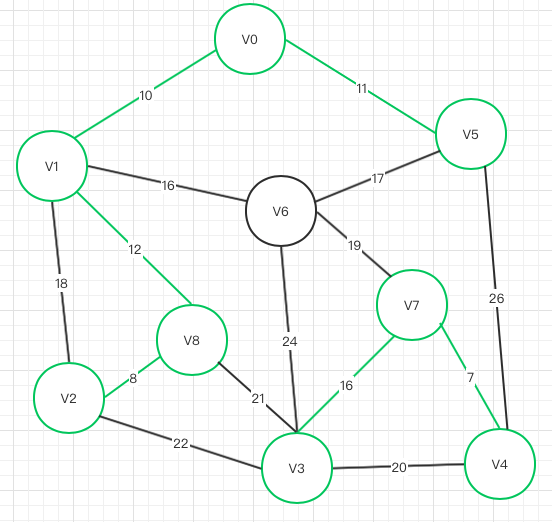
V1->V6

不存在闭环，可以联通

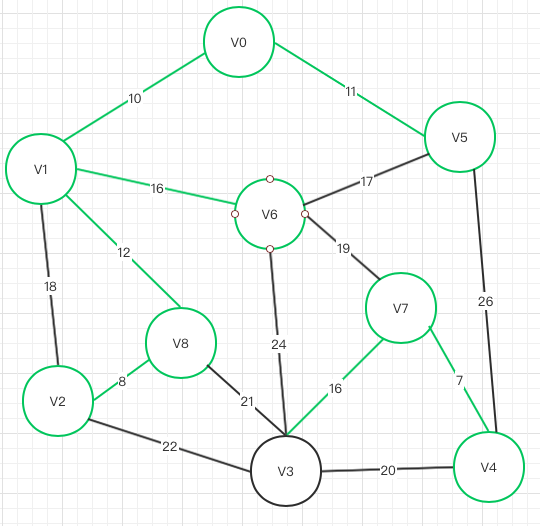
V5->V6

存在闭环，不可联通！！ V0 V1 V6 V5 成闭环

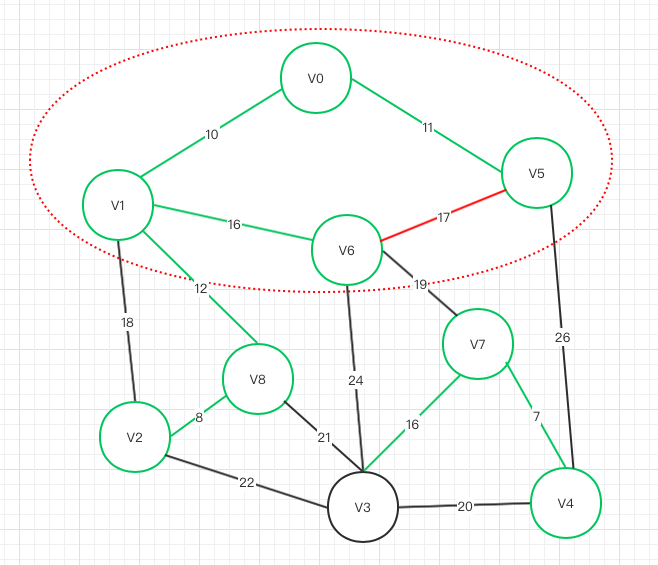
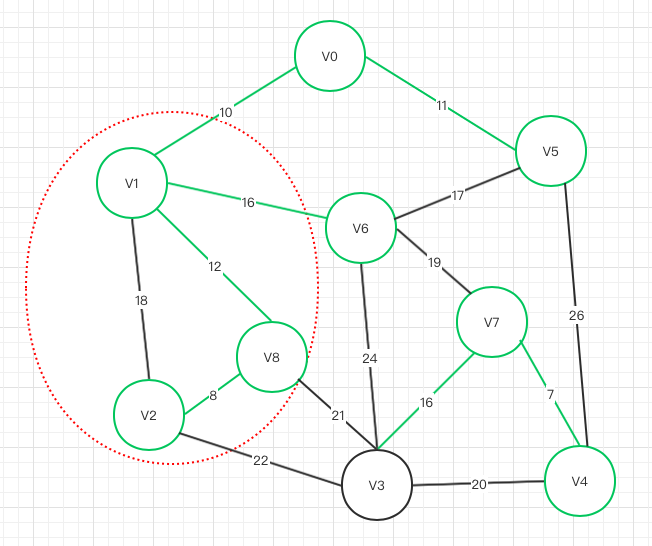
V1->V2

存在闭环，不可联通！！ V1 V2 V8 成闭环

V6->V7

不存在闭环，可以联通

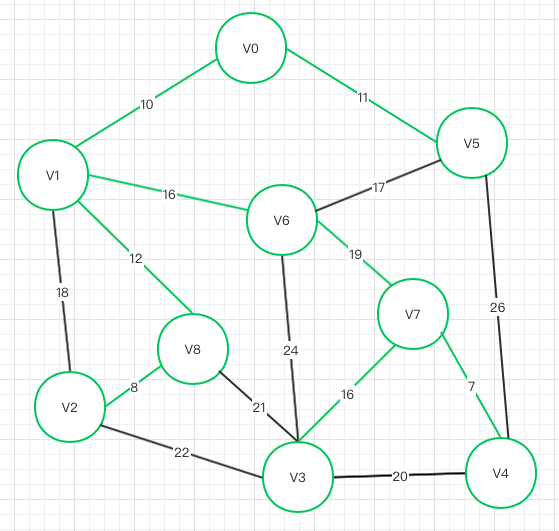
此时，所有结点均以走通结束

代码

#include "stdio.h"
#include "stdlib.h"

#include "math.h"
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXEDGE 20
#define MAXVEX 20
#define INFINITYC 65535

typedef int Status;
typedef struct
{
    int arc[MAXVEX][MAXVEX];
    int numVertexes, numEdges;
}MGraph;

/* 对边集数组Edge结构的定义 */
typedef struct
{
    int begin;
    int end;
    int weight;
}Edge ;

排序

/* 交换权值以及头和尾 */
void Swapn(Edge *edges,int i, int j)
{
    int tempValue;
    
    //交换edges[i].begin 和 edges[j].begin 的值
    tempValue = edges[i].begin;
    edges[i].begin = edges[j].begin;
    edges[j].begin = tempValue;
    
    //交换edges[i].end 和 edges[j].end 的值
    tempValue = edges[i].end;
    edges[i].end = edges[j].end;
    edges[j].end = tempValue;
    
    //交换edges[i].weight 和 edges[j].weight 的值
    tempValue = edges[i].weight;
    edges[i].weight = edges[j].weight;
    edges[j].weight = tempValue;
}

/* 对权值进行排序 */
void sort(Edge edges[],MGraph *G)
{
    //对权值进行排序(从小到大)
    int i, j;
    for ( i = 0; i < G->numEdges; i++)
    {
        for ( j = i + 1; j < G->numEdges; j++)
        {
            if (edges[i].weight > edges[j].weight)
            {
                Swapn(edges, i, j);
            }
        }
    }
    
    printf("边集数组根据权值排序之后的为:\n");
    for (i = 0; i < G->numEdges; i++)
    {
        printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
    }
    
}

/// 查找连线顶点的尾部下标，帮助判断是否会构成闭环
/// @param parent 存储结点互相关联的数组
/// @param f 定点下标
int Find(int *parent, int f)
{
    while ( parent[f] > 0)
    {
        f = parent[f];
    }
    return f;
}

/* 生成最小生成树 */
void MiniSpanTree_Kruskal(MGraph G)
{
    int i, j, n, m;
    int sum = 0;
    int k = 0;
    /* 定义一数组用来判断边与边是否形成环路
     用来记录顶点间的连接关系. 通过它来防止最小生成树产生闭环;*/
    
    int parent[MAXVEX];
    /* 定义边集数组,edge的结构为begin,end,weight,均为整型 */
    Edge edges[MAXEDGE];
    
    /*1. 用来构建边集数组*/
    for ( i = 0; i < G.numVertexes-1; i++)
    {
        for (j = i + 1; j < G.numVertexes; j++)
        {
            //如果当前路径权值 != ∞
            if (G.arc[i][j]<INFINITYC)
            {
                //将路径对应的begin,end,weight 存储到edges 边集数组中.
                edges[k].begin = i;
                edges[k].end = j;
                edges[k].weight = G.arc[i][j];
                
                //边集数组计算器k++;
                k++;
            }
        }
    }
    
    //2. 对边集数组排序
    sort(edges, &G);
    
    
    //3.初始化parent 数组为0. 9个顶点;
    // for (i = 0; i < G.numVertexes; i++)
    for (i = 0; i < MAXVEX; i++)
        parent[i] = 0;
    
    //4. 计算最小生成树
    printf("打印最小生成树：\n");
    /* 循环每一条边 G.numEdges 有15条边*/
    for (i = 0; i < G.numEdges; i++)
    {
        //获取begin,end 在parent 数组中的信息;
        //如果n = m ,将begin 和 end 连接,就会产生闭合的环.
        n = Find(parent,edges[i].begin);
        m = Find(parent,edges[i].end);
        //printf("n = %d,m = %d\n",n,m);
        
        /* 假如n与m不等，说明此边没有与现有的生成树形成环路 */
        if (n != m)
        {
            /* 将此边的结尾顶点放入下标为起点的parent中。 */
            /* 表示此顶点已经在生成树集合中 */
            parent[n] = m;
            
            /*打印最小生成树路径*/
            printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
            sum += edges[i].weight;
        }
    }
    
    printf("sum = %d\n",sum);
}

图的最小生成树——Prim算法、Kruskal算法

Prim算法

注意⚠️：绿色代表已联通，红色代表下一轮的可选边和结点，黑色线表示不可联通或暂未联通

第一轮 从V0开始

第二轮

第三轮

第四轮

第五轮

第六轮

第七轮

第八轮

代码实现思路

kruskal算法

算法思路

注意⚠️ parent 数组的目的是为了判断当前的边是否会构成闭环

1、将邻接矩阵转化成边表数组，对边表数组根据权值按照从⼩小到⼤大的顺序排序;

2、开始生成：条件是思路中的3和4

按照上面的排序，V4->V7

V2->V8

V0->V1

V0->V5

V1->V8

V3->V7

V1->V6

V5->V6

V1->V2

V6->V7

代码

第一轮从V0开始